高中数学人教A版必修1第三章3.1.1 方程的根与函数的零点 说课课件 (24张PPT)
文档属性
| 名称 | 高中数学人教A版必修1第三章3.1.1 方程的根与函数的零点 说课课件 (24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 336.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览





文档简介
3.1.1 方程的根与函数的零点
一、说教材
本节课是学生在初中学习的各种方程、并掌握了一些方程的求根公式,又在高中阶段学习了函数的定义、表示,以及初等函数的图像和性质的基础上,进一步讨论方程的根与函数的零点问题.
同时它为后续学习二分法求方程的近似解奠定基础,本节内容起着承上启下的作用.
函数是高中数学的重要组成部分,本节课是函数与方程的紧密结合.
1.1 本节课的地
位和作用
学生虽然在函数与方程方面有了一定的基础,但对于高一学生,他们的思维习惯、动手作图能力以及观察、归纳、转化等能力都还不强,数学抽象和逻辑推理能力欠缺!引导学生学会探究和解决问题的方法和策略,让他们感受知识的发生、发展的过程,在体验中构建自己的知识体系.
1.2 学情分析
一、说教材
1.3 教学目标
一、说教材
1.理解函数零点的概念以及函数零点与方程根的关系;
2.会求函数的零点;
3.掌握函数零点存在性定理并会判断零点的个数及零点所在区间;
4.积极参与由特殊到一般的探究问题的过程中感受学习、探索、发现的乐趣;
5.体会函数方程思想,数形结合思想,化归转化思想的应用,培养学生的数学抽象,逻辑思维和直观想象能力.
1.理解函数零点的概念以及函数零点与方程根的关系;
2.掌握函数零点存在性定理.
理解函数零点存在的判定条件.
一、说教材
1.4 教学重难点
教法:问题引导法;
学法:小组讨论法;
评价:自我展示.
一、说教材
1.5 教法、学法和教具准备
教具准备:直尺、PPT;
二、说教学过程
我的教学过程总的来说有2个探究,2个新概念,4 个典例,7个问题来引导教学!
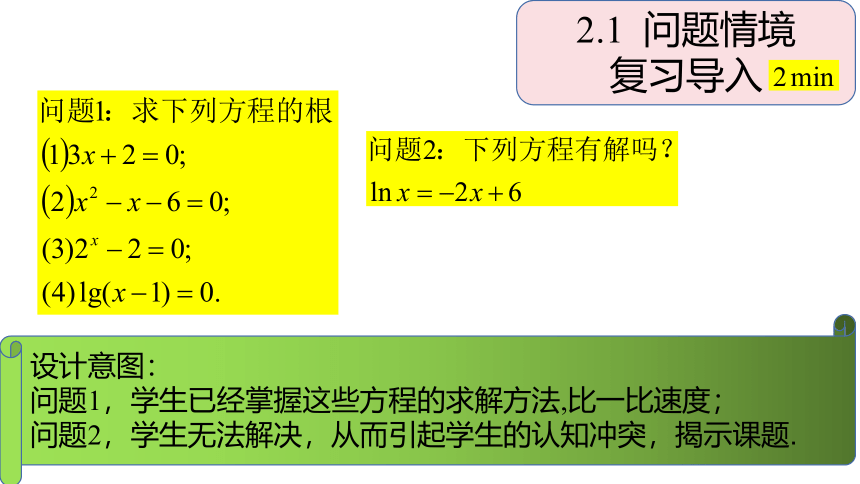
2.1 问题情境
复习导入
设计意图:
问题1,学生已经掌握这些方程的求解方法,比一比速度;
问题2,学生无法解决,从而引起学生的认知冲突,揭示课题.
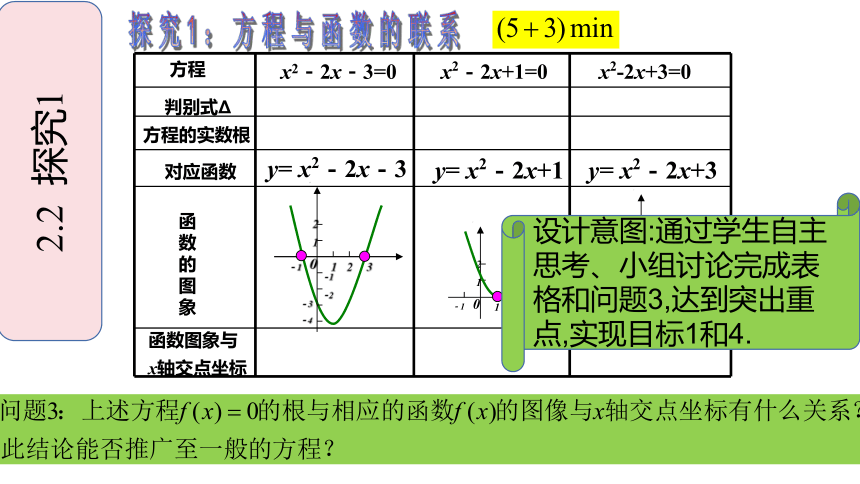
探究1:方程与函数的联系
方程
x2-2x+1=0
x2-2x+3=0
对应函数
函
数
的
图
象
方程的实数根
x2-2x-3=0
y= x2-2x-3
y= x2-2x+1
y= x2-2x+3
x
y
0
-1
3
2
1
1
2
5
4
3
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
y
x
0
-1
2
1
1
2
函数图象与
x轴交点坐标
判别式Δ
2.2 探究1
设计意图:通过学生自主思考、小组讨论完成表格和问题3,达到突出重点,实现目标1和4.
函数的零点定义:
对于函数y=f(x),我们把使f(x)=0的实数x,叫做函数y=f(x)的零点.
问题4:函数y=f(x)的零点是点吗?
2.3 引出零点概念
问题4设计意图:强调易错点
等价关系:
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
问题5:是不是所有的函数都有零点?举例说明.
问题5设计意图:
重在发散学生思维!预设举例:二次函数当判别式<0,指数函数,对数函数、一次函数等可以限制定义域......
效果检测:
2.4 效果检测
预设1.再次强调函数的零点不是点是数!
2.设计意图:以计算题为主,学生自己思考、展示,实现目标2及培养逻辑思维能力.
探究2:函数零点存在性问题
x
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
y
2.5 探究2
设计意图:通过自主思考、分组讨论找到零点存在性定理的条件,此法是由特殊到一般的探究的过程.
函数零点存在性定理:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点。
即存在 c∈(a,b) ,使得 f(c) =0,这个c也就是方程 f(x)=0 的根.
2.6 函数零点存在性定理
预设:强调两个条件缺一不可!深刻理解定理内容!
设计意图:强调函数思想,实现目标3,4,突破难点.
1.问题6为了表明零点存在性定理只能说明存在零点,但不能说明存在几个零点;
2.问题7为了说明定理的条件充分而不必要,培养学生的逻辑思维能力.
a
b x
a
b x
A
B
A
B
a
b x
A
B
至少有一个零点
不一定存在零点
不一定存在零点
A
B
设计意图:
学生自己尝试画,从而深刻理解零点的个数和定理的不可逆.
3.求函数 零点的个数.
解 :用计算机做出x、f(x)对应值表和图象如下:
x
1
2
3
4
5
6
7
8
9
f(x)
-4
-1.3
1.1
3.4
5.6
7.8
9.9
12.1
14.2
10
8
6
4
2
-2
-4
5
1
2
3
4
6
x
y
O
由表和图象可知,f(2)<0,f(3)>0,f(2)f(3)<0,这说明函数f(x)在区间(2,3)内有零点.
因为函数f(x)在(0,+∞)内单调递增,所以它仅有一个零点.
效果检测:
2.7 典例剖析
预设:增函数+增函数=增函数.并强调定义域!
解法二 :
确定函数f(x)=lnx+2x-6零点的个数
6
O
x
1
2
3
4
y
y=lnx
y=-2x+6
由图可知,两函数图象只有一个交点,即方程只有一根,并且根在区间(2,3)内.
确定方程lnx+2x-6=0的根的个数
求lnx=6-2x的根的个数
判断函数y=lnx与y=6-2x两图象交点个数
预设:老师板书画图,起到示范作用!本题突出了化归转化的数学思想!
你能找到这个方程的一个有解区间吗?
设计意图:回到开始的问题,做到首尾呼应,同时为下节课二分法奠定基础!
设计意图:
再次巩固提升!
知识内容
思想与方法
函数的零点
数形结合
函数与方程
化归与转化
函数零点存在性定理
题型
设计意图:
学生自主归纳,实现了本节课的学习目标!
2.8 课堂小结
2.9 作业布置
设计意图:
紧扣本节知识,达到举一反三!
3.1.1方程的根与函数的零点
增函数+增函数=增函数
示范3题法2画图
一.函数的零点
二.零点存在性定理
学生
板演
2(1)(2)4题
2.10 板书设计
设计意图:
重点突出,美观清晰!
谢谢大家!
一、说教材
本节课是学生在初中学习的各种方程、并掌握了一些方程的求根公式,又在高中阶段学习了函数的定义、表示,以及初等函数的图像和性质的基础上,进一步讨论方程的根与函数的零点问题.
同时它为后续学习二分法求方程的近似解奠定基础,本节内容起着承上启下的作用.
函数是高中数学的重要组成部分,本节课是函数与方程的紧密结合.
1.1 本节课的地
位和作用
学生虽然在函数与方程方面有了一定的基础,但对于高一学生,他们的思维习惯、动手作图能力以及观察、归纳、转化等能力都还不强,数学抽象和逻辑推理能力欠缺!引导学生学会探究和解决问题的方法和策略,让他们感受知识的发生、发展的过程,在体验中构建自己的知识体系.
1.2 学情分析
一、说教材
1.3 教学目标
一、说教材
1.理解函数零点的概念以及函数零点与方程根的关系;
2.会求函数的零点;
3.掌握函数零点存在性定理并会判断零点的个数及零点所在区间;
4.积极参与由特殊到一般的探究问题的过程中感受学习、探索、发现的乐趣;
5.体会函数方程思想,数形结合思想,化归转化思想的应用,培养学生的数学抽象,逻辑思维和直观想象能力.
1.理解函数零点的概念以及函数零点与方程根的关系;
2.掌握函数零点存在性定理.
理解函数零点存在的判定条件.
一、说教材
1.4 教学重难点
教法:问题引导法;
学法:小组讨论法;
评价:自我展示.
一、说教材
1.5 教法、学法和教具准备
教具准备:直尺、PPT;
二、说教学过程
我的教学过程总的来说有2个探究,2个新概念,4 个典例,7个问题来引导教学!
2.1 问题情境
复习导入
设计意图:
问题1,学生已经掌握这些方程的求解方法,比一比速度;
问题2,学生无法解决,从而引起学生的认知冲突,揭示课题.
探究1:方程与函数的联系
方程
x2-2x+1=0
x2-2x+3=0
对应函数
函
数
的
图
象
方程的实数根
x2-2x-3=0
y= x2-2x-3
y= x2-2x+1
y= x2-2x+3
x
y
0
-1
3
2
1
1
2
5
4
3
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
y
x
0
-1
2
1
1
2
函数图象与
x轴交点坐标
判别式Δ
2.2 探究1
设计意图:通过学生自主思考、小组讨论完成表格和问题3,达到突出重点,实现目标1和4.
函数的零点定义:
对于函数y=f(x),我们把使f(x)=0的实数x,叫做函数y=f(x)的零点.
问题4:函数y=f(x)的零点是点吗?
2.3 引出零点概念
问题4设计意图:强调易错点
等价关系:
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
问题5:是不是所有的函数都有零点?举例说明.
问题5设计意图:
重在发散学生思维!预设举例:二次函数当判别式<0,指数函数,对数函数、一次函数等可以限制定义域......
效果检测:
2.4 效果检测
预设1.再次强调函数的零点不是点是数!
2.设计意图:以计算题为主,学生自己思考、展示,实现目标2及培养逻辑思维能力.
探究2:函数零点存在性问题
x
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
y
2.5 探究2
设计意图:通过自主思考、分组讨论找到零点存在性定理的条件,此法是由特殊到一般的探究的过程.
函数零点存在性定理:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点。
即存在 c∈(a,b) ,使得 f(c) =0,这个c也就是方程 f(x)=0 的根.
2.6 函数零点存在性定理
预设:强调两个条件缺一不可!深刻理解定理内容!
设计意图:强调函数思想,实现目标3,4,突破难点.
1.问题6为了表明零点存在性定理只能说明存在零点,但不能说明存在几个零点;
2.问题7为了说明定理的条件充分而不必要,培养学生的逻辑思维能力.
a
b x
a
b x
A
B
A
B
a
b x
A
B
至少有一个零点
不一定存在零点
不一定存在零点
A
B
设计意图:
学生自己尝试画,从而深刻理解零点的个数和定理的不可逆.
3.求函数 零点的个数.
解 :用计算机做出x、f(x)对应值表和图象如下:
x
1
2
3
4
5
6
7
8
9
f(x)
-4
-1.3
1.1
3.4
5.6
7.8
9.9
12.1
14.2
10
8
6
4
2
-2
-4
5
1
2
3
4
6
x
y
O
由表和图象可知,f(2)<0,f(3)>0,f(2)f(3)<0,这说明函数f(x)在区间(2,3)内有零点.
因为函数f(x)在(0,+∞)内单调递增,所以它仅有一个零点.
效果检测:
2.7 典例剖析
预设:增函数+增函数=增函数.并强调定义域!
解法二 :
确定函数f(x)=lnx+2x-6零点的个数
6
O
x
1
2
3
4
y
y=lnx
y=-2x+6
由图可知,两函数图象只有一个交点,即方程只有一根,并且根在区间(2,3)内.
确定方程lnx+2x-6=0的根的个数
求lnx=6-2x的根的个数
判断函数y=lnx与y=6-2x两图象交点个数
预设:老师板书画图,起到示范作用!本题突出了化归转化的数学思想!
你能找到这个方程的一个有解区间吗?
设计意图:回到开始的问题,做到首尾呼应,同时为下节课二分法奠定基础!
设计意图:
再次巩固提升!
知识内容
思想与方法
函数的零点
数形结合
函数与方程
化归与转化
函数零点存在性定理
题型
设计意图:
学生自主归纳,实现了本节课的学习目标!
2.8 课堂小结
2.9 作业布置
设计意图:
紧扣本节知识,达到举一反三!
3.1.1方程的根与函数的零点
增函数+增函数=增函数
示范3题法2画图
一.函数的零点
二.零点存在性定理
学生
板演
2(1)(2)4题
2.10 板书设计
设计意图:
重点突出,美观清晰!
谢谢大家!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
