高中数学人教A版必修4第二章平面向量数量积课件(12张PPT)
文档属性
| 名称 | 高中数学人教A版必修4第二章平面向量数量积课件(12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 894.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 21:04:18 | ||
图片预览




文档简介
平面向量的数量积
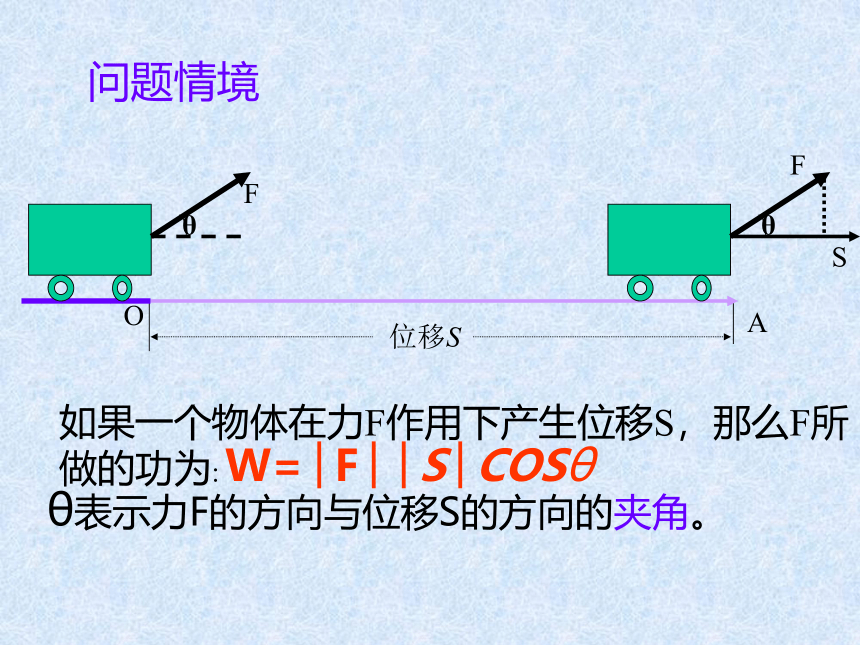
如果一个物体在力F作用下产生位移S,那么F所做的功为:
θ表示力F的方向与位移S的方向的夹角。
位移S
O
A
问题情境
θ
F
F
θ
S
W=│F││S│COSθ
1、向量的夹角是如何定义(规定)的?
2、向量的数量积如何定义,它与两个向量的加减法有什么本质区别?
3、向量的数量积是向量吗?向量在方向上 的投影是向量吗?
4、平面向量的数量积有什么样的几何意义?
小组讨论
(当 时,a与b__;当 时,a与b__;当 时,a与b__,记作 )
反向
同向
垂直
指出下列图中两向量的夹角
A
O
A
B
B
B
B
.
A
A
O
O
O
.
(2)
(4)
(3)
(1)
(4)中 与 的夹角为θ
已知两个非零向量a和b,在平上任取一点O, =a, =b,则 叫做 向量a与b的夹角
(1)中 与 的夹角为
(2)中 与 的夹角为
(3)中 与 的夹角为
1、向量的夹角
思考1:在平面向量的数量积定义中,它与两个向量的加减法有什么本质区别?
向量的加减的结果还是向量,但向量的数量积结果是一个数量(实数)。
(这个数量的大小与两个向量的长度及其夹角有关)
已知两个非零向量a和b,它们的夹角为 ,我们 把数量 叫做向量a与b的数量积(或内积) 记作 即
2、数量积的定义
规定: 0
│b│COSθ叫做向量b在向量a上的投影。
(1)
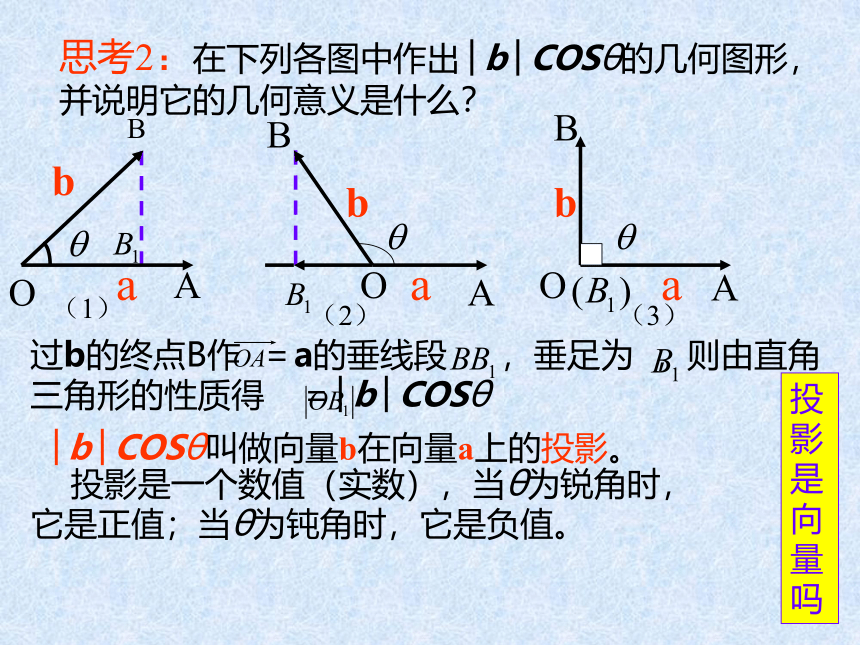
思考2:在下列各图中作出│b│COSθ的几何图形,并说明它的几何意义是什么?
O
A
B
(2)
a
b
O
A
B
(3)
a
b
a
b
A
O
投影是向量吗
投影是一个数值(实数),当θ为锐角时,它是正值;当θ为钝角时,它是负值。
过b的终点B作 =a的垂线段 ,垂足为 ,则由直角三角形的性质得 =│b│COSθ
B
数量积a?b等于a的长度│a│与b在a的方向上的投影│b│COSθ的积
a?b的几何意义:
3、向量数量积的几何意义
a?b=│a││b│COSθ
a
b
θ
O
B
OB= │b│COSθ
4、向量数量积的运算律
(1) a?b= (交换律)
(2)(λa) ?b= = (数乘结合律)
(3)(a+b)?c= (分配律)
λ(a?b)
a?(λb)
b?a
a?c+b?c
5、向量数量积的性质
设a,b都是非零向量,e是与b的方向相同的单位向量,θ是a与e的夹角,则 (1)e?a=a?e=_________
(2)a b____a?b=0
(3)当a与b同向时,a?b=________
当a与b异向时,a?b=___________
a?a=________
(4) │ a?b │___ │a││b│
(5)cos =
______
│a│COSθ
│a││b│
-│a││b│
性质4
a?b=│a│b│COSθ
(1)若a=0,则对任意向量b,有a?b=0 ( )
(2)若a 0,则对任意非零向量b,有a? b 0
( )
(3)若a 0,且a?b=0,则b=0 ( )
(4)若a?b=0 ,则a=0或b=0 ( )
(5)对任意向量a有 ( )
(
6、反馈练习:判断正误
a?=|a|?
×
×
×
√
√
向量的数量积是向量之间的一种乘法,与数的乘法是有区别的
7、作业布置
《教学导案》P82随堂训练 1、4、6
P83强化训练 2、8
谢谢大家!
如果一个物体在力F作用下产生位移S,那么F所做的功为:
θ表示力F的方向与位移S的方向的夹角。
位移S
O
A
问题情境
θ
F
F
θ
S
W=│F││S│COSθ
1、向量的夹角是如何定义(规定)的?
2、向量的数量积如何定义,它与两个向量的加减法有什么本质区别?
3、向量的数量积是向量吗?向量在方向上 的投影是向量吗?
4、平面向量的数量积有什么样的几何意义?
小组讨论
(当 时,a与b__;当 时,a与b__;当 时,a与b__,记作 )
反向
同向
垂直
指出下列图中两向量的夹角
A
O
A
B
B
B
B
.
A
A
O
O
O
.
(2)
(4)
(3)
(1)
(4)中 与 的夹角为θ
已知两个非零向量a和b,在平上任取一点O, =a, =b,则 叫做 向量a与b的夹角
(1)中 与 的夹角为
(2)中 与 的夹角为
(3)中 与 的夹角为
1、向量的夹角
思考1:在平面向量的数量积定义中,它与两个向量的加减法有什么本质区别?
向量的加减的结果还是向量,但向量的数量积结果是一个数量(实数)。
(这个数量的大小与两个向量的长度及其夹角有关)
已知两个非零向量a和b,它们的夹角为 ,我们 把数量 叫做向量a与b的数量积(或内积) 记作 即
2、数量积的定义
规定: 0
│b│COSθ叫做向量b在向量a上的投影。
(1)
思考2:在下列各图中作出│b│COSθ的几何图形,并说明它的几何意义是什么?
O
A
B
(2)
a
b
O
A
B
(3)
a
b
a
b
A
O
投影是向量吗
投影是一个数值(实数),当θ为锐角时,它是正值;当θ为钝角时,它是负值。
过b的终点B作 =a的垂线段 ,垂足为 ,则由直角三角形的性质得 =│b│COSθ
B
数量积a?b等于a的长度│a│与b在a的方向上的投影│b│COSθ的积
a?b的几何意义:
3、向量数量积的几何意义
a?b=│a││b│COSθ
a
b
θ
O
B
OB= │b│COSθ
4、向量数量积的运算律
(1) a?b= (交换律)
(2)(λa) ?b= = (数乘结合律)
(3)(a+b)?c= (分配律)
λ(a?b)
a?(λb)
b?a
a?c+b?c
5、向量数量积的性质
设a,b都是非零向量,e是与b的方向相同的单位向量,θ是a与e的夹角,则 (1)e?a=a?e=_________
(2)a b____a?b=0
(3)当a与b同向时,a?b=________
当a与b异向时,a?b=___________
a?a=________
(4) │ a?b │___ │a││b│
(5)cos =
______
│a│COSθ
│a││b│
-│a││b│
性质4
a?b=│a│b│COSθ
(1)若a=0,则对任意向量b,有a?b=0 ( )
(2)若a 0,则对任意非零向量b,有a? b 0
( )
(3)若a 0,且a?b=0,则b=0 ( )
(4)若a?b=0 ,则a=0或b=0 ( )
(5)对任意向量a有 ( )
(
6、反馈练习:判断正误
a?=|a|?
×
×
×
√
√
向量的数量积是向量之间的一种乘法,与数的乘法是有区别的
7、作业布置
《教学导案》P82随堂训练 1、4、6
P83强化训练 2、8
谢谢大家!
