高中数学人教A版必修5第三章 不等式 3.4 基本不等式 课件(16张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第三章 不等式 3.4 基本不等式 课件(16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 733.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 21:08:00 | ||
图片预览






文档简介
为了赛制的公平公正,参赛学校请:
统一使用此模版作为PPT展示
封面上请不要标注“xxx学校”
开始说课只需报抽签后的出场代码
学习目标
会推导基本不等式
理解基本不等式的几何意义
会利用基本不等式求最值
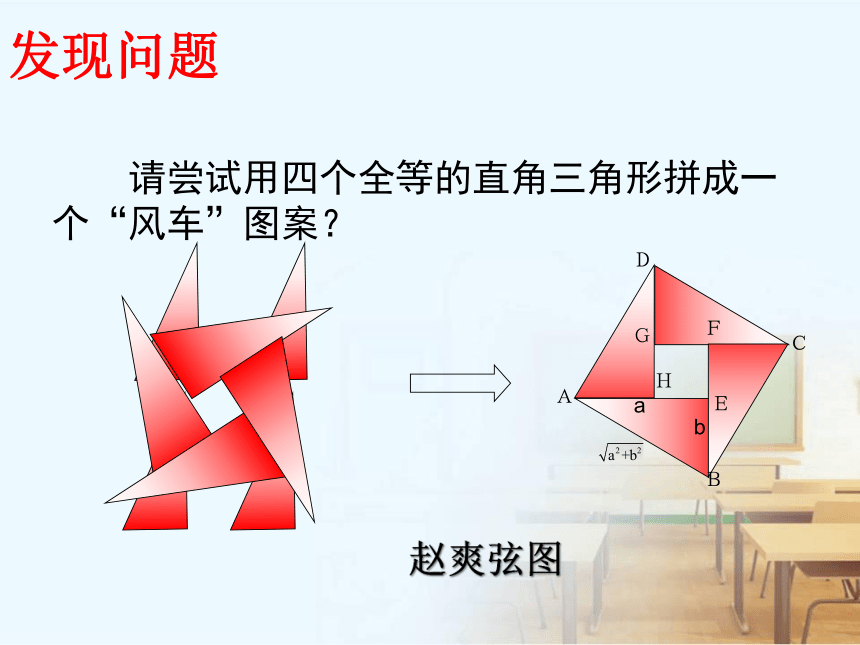
请尝试用四个全等的直角三角形拼成一个“风车”图案?
发现问题
A
B
C
E
D
G
F
a
H
b
赵爽弦图
正方形ABCD中设AE=a,BE=b,则正方形的面积为___
Rt△ABE,Rt△BCF,Rt△CDG,Rt△ADH是全等三角形,
它们的面积之和是___
很明显:______
问题1:它们有相等的情况吗?何时相等?
问题2:当 a,b为任意实数时,
上式还成立吗?如何证明?
A
B
C
E
D
G
F
a
H
b
发现问题
发现问题
定理:
一般地,对于任意实数a、b,有
当且仅当(重点强调)a=b时,等号成立
如果用 替换a,b,能得到什么结论?前提条件是什么?
基本不等式:若
当且仅当a=b时,等号成立
——请同学们结合导学案,用8分钟的时间合作讨论,整理出证明方法。
探讨新知
问题3:你能证明基本不等式吗?有哪些证明方法?
证法一:( )
证法二:( )
要证,
即证,
只要证,
探讨新知
作差法
分析法
显然成立
当且仅当a=b时,等号成立
证法三:( )
探讨新知
几何法
A
C
D
E
a
b
B
如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____
基本不等式的几何意义:
半弦不大于半径
例1、求函数 的值域。
变式1、求函数 的最小值。
合作交流
答案:
(思考:为什么不能用基本不等式)
不满足
————应用基本不等式第一个限制条件:
既“一正”
例2、已知 且 ,求 的最小值。
变式2、若本例改成已知 ,求 的最小值。可做么?为什么?
变式3、已知 且 ,求 的最大值
合作交流
解:因为 ,
由基本不等式可得:
当且仅当 时,取最小值。
————基本不等式求最值的第二个限制条件:有定值,
既“二定”
————“积定和最小,和定积最大”
例3、已知 ,求函数 的值域。
合作交流
解:令 ,则
由“对勾函数”性质可得:
在 上单调递增,则
所以 的值域为
————基本不等式求最值的第三个限制条件:
当且仅当a=b时取等号
既“三相等”
用基本不等式求最值的三个限制条件:
一正:
二定:积定和最小,和定积最大
三相等:当且仅当a=b时取等号
合作交流
练习1、若实数 ,求 的最小值
练习2、1.用篱笆围一个面积为100的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短,最短的篱笆是多少?
2.一段长为36的篱笆围成一个矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
课堂检测
答案:
答案:1.长宽都为10m时,篱笆最短为40m;
2. 长宽都为9m时,面积最大为81
请同学们结合导学案完成以下问题:
1.基本不等式的内容:
2.基本不等式的几何解释:
3.基本不等式应用的限制条件:
课堂小结
练习题:习题3.4A组1,2,4
思考题:1、若 ,则求 的最小值
2、已知 ,求 的最小值
课后作业
统一使用此模版作为PPT展示
封面上请不要标注“xxx学校”
开始说课只需报抽签后的出场代码
学习目标
会推导基本不等式
理解基本不等式的几何意义
会利用基本不等式求最值
请尝试用四个全等的直角三角形拼成一个“风车”图案?
发现问题
A
B
C
E
D
G
F
a
H
b
赵爽弦图
正方形ABCD中设AE=a,BE=b,则正方形的面积为___
Rt△ABE,Rt△BCF,Rt△CDG,Rt△ADH是全等三角形,
它们的面积之和是___
很明显:______
问题1:它们有相等的情况吗?何时相等?
问题2:当 a,b为任意实数时,
上式还成立吗?如何证明?
A
B
C
E
D
G
F
a
H
b
发现问题
发现问题
定理:
一般地,对于任意实数a、b,有
当且仅当(重点强调)a=b时,等号成立
如果用 替换a,b,能得到什么结论?前提条件是什么?
基本不等式:若
当且仅当a=b时,等号成立
——请同学们结合导学案,用8分钟的时间合作讨论,整理出证明方法。
探讨新知
问题3:你能证明基本不等式吗?有哪些证明方法?
证法一:( )
证法二:( )
要证,
即证,
只要证,
探讨新知
作差法
分析法
显然成立
当且仅当a=b时,等号成立
证法三:( )
探讨新知
几何法
A
C
D
E
a
b
B
如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____
基本不等式的几何意义:
半弦不大于半径
例1、求函数 的值域。
变式1、求函数 的最小值。
合作交流
答案:
(思考:为什么不能用基本不等式)
不满足
————应用基本不等式第一个限制条件:
既“一正”
例2、已知 且 ,求 的最小值。
变式2、若本例改成已知 ,求 的最小值。可做么?为什么?
变式3、已知 且 ,求 的最大值
合作交流
解:因为 ,
由基本不等式可得:
当且仅当 时,取最小值。
————基本不等式求最值的第二个限制条件:有定值,
既“二定”
————“积定和最小,和定积最大”
例3、已知 ,求函数 的值域。
合作交流
解:令 ,则
由“对勾函数”性质可得:
在 上单调递增,则
所以 的值域为
————基本不等式求最值的第三个限制条件:
当且仅当a=b时取等号
既“三相等”
用基本不等式求最值的三个限制条件:
一正:
二定:积定和最小,和定积最大
三相等:当且仅当a=b时取等号
合作交流
练习1、若实数 ,求 的最小值
练习2、1.用篱笆围一个面积为100的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短,最短的篱笆是多少?
2.一段长为36的篱笆围成一个矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
课堂检测
答案:
答案:1.长宽都为10m时,篱笆最短为40m;
2. 长宽都为9m时,面积最大为81
请同学们结合导学案完成以下问题:
1.基本不等式的内容:
2.基本不等式的几何解释:
3.基本不等式应用的限制条件:
课堂小结
练习题:习题3.4A组1,2,4
思考题:1、若 ,则求 的最小值
2、已知 ,求 的最小值
课后作业
