高中数学人教A版必修5第三章不等式 3.4 基本不等式 课件(19张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第三章不等式 3.4 基本不等式 课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 21:11:22 | ||
图片预览




文档简介
为了赛制的公平公正,参赛学校请:
统一使用此模版作为PPT展示
封面上请不要标注“xxx学校”
开始说课只需报抽签后的出场代码
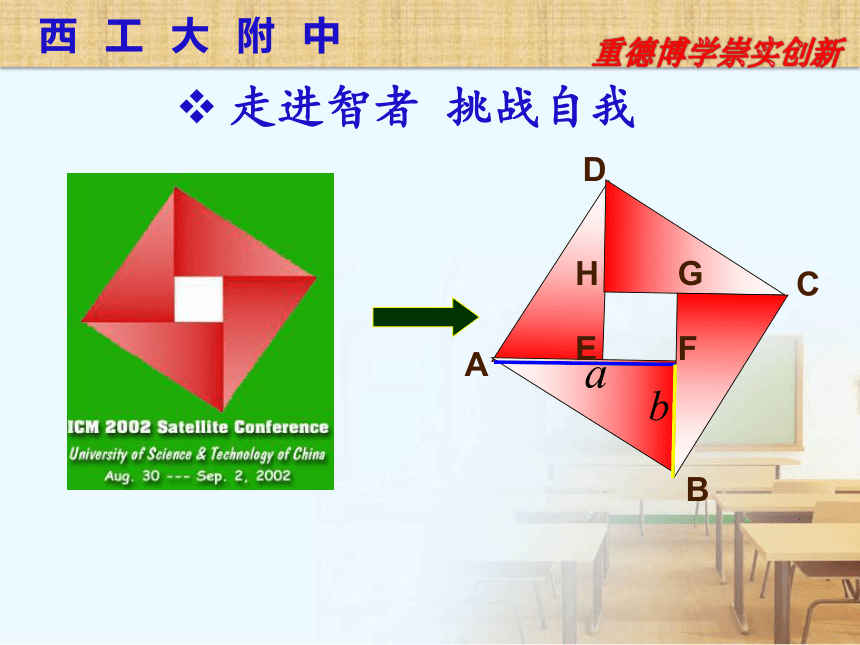
这是2002年在北京召开的第24届国际数学家大会会标.会标根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。
走进智者 挑战自我
走进生活 感悟数学
1.知识与技能:学会推导并掌握基本不等式,
理解基本不等式的几何意义,会用基
本不等式求最值、证明不等式;
2.过程和方法:培养观察、试验、归纳、判
断、猜想的思维能力;
3:情感、态度和价值观:敢于探索,体会
数与形的和谐统一,领略数学的应用
价值。
学习目标
A
B
C
D
E
F
G
H
走进智者 挑战自我
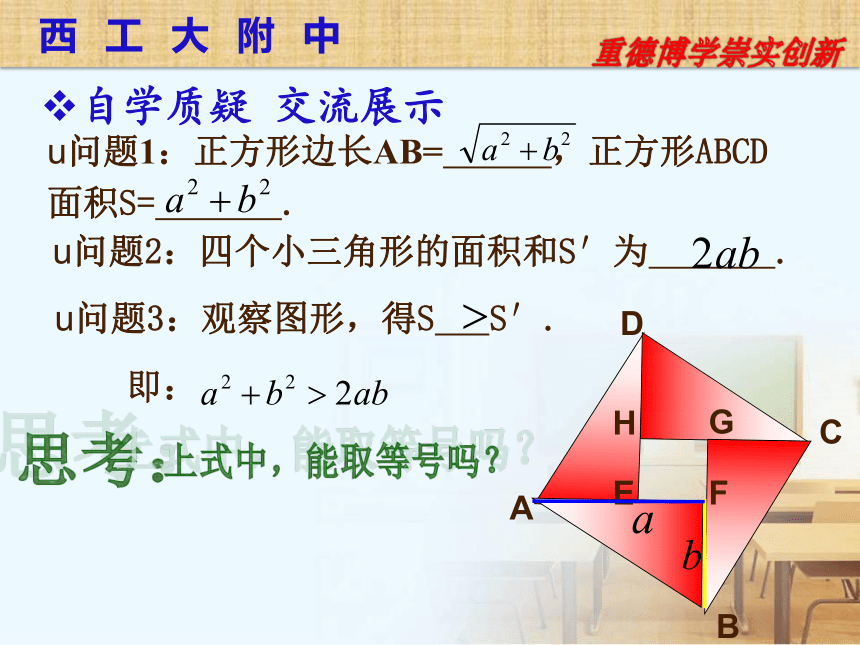
自学质疑 交流展示
问题1:正方形边长AB= ,正方形ABCD面积S= .
问题2:四个小三角形的面积和S′为 .
问题3:观察图形,得S S′.
即:
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
A
B
C
D
E(FGH)
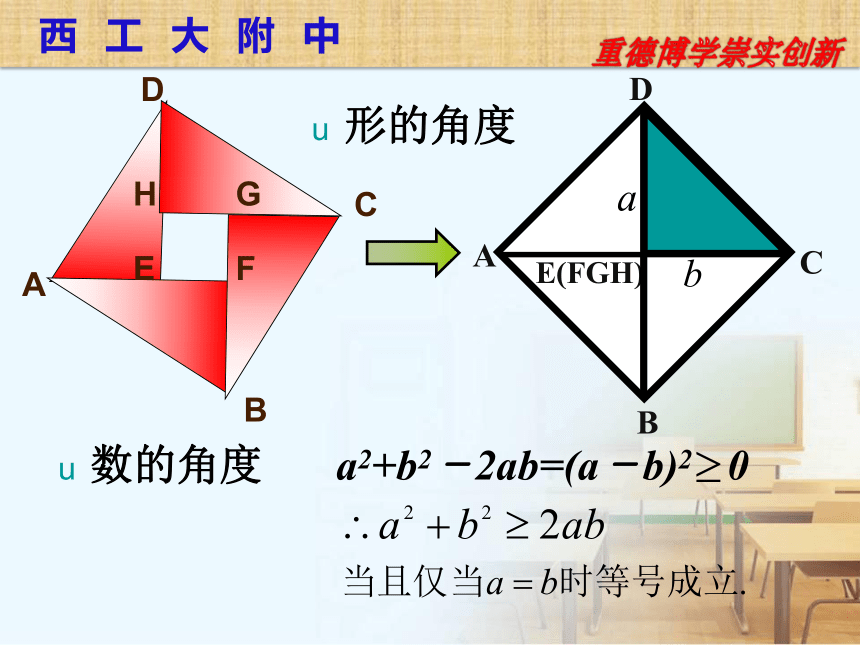
形的角度
数的角度
a2+b2-2ab=(a-b)2 0
当 为任意实数时,
都成立吗?
结论:一般地,对于任意实数 ,我们有
当且仅当 时,等号成立.
重要不等式
探究
我们称上述不等式为基本不等式,
其中 叫做 的算术平均数
叫做 的几何平均数
也叫均值不等式.
E
刨根问底 加深理解
观察图:AB是圆O的直径,DE是垂直于直径的弦,其中AC=a,BC=b,讨论下列问题:
讨论
问题1:你能用a、b表示线段OD和DC吗? OD= ,DC= .
问题2:能从图形中得出DC和OD的大小关系吗?
问题3:你能给出基本不等式的的几何解释吗?
几何解释
圆的半径不小于圆内半弦长.
适用范围
文字叙述
“=”成立条件
两数的平方和不小于它们积的2倍
两个正数的算术平均数不小于它们的几何平均数
填表比较:
公式理解
下面说法正确吗?
√
不等式中,不等关
系与字母形式无关
√
√
×
举一反三 学以致用
例1.(1)用篱笆围一个面积为100㎡的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短.最短篱笆是多少?
解 设矩形菜园的长为 m,宽为 m,
则 ,
篱笆长为 m.
因此,这个矩形的长、宽各为10m时,所用篱笆最短.最短篱笆是40m.
积定和最小
积为定值
例1.(2)一个长为36m的篱笆围一个的矩形菜园,问这个矩形的长、宽各为多少时,菜园面积最大.最大面积是多少?
解 设矩形菜园的长为 m,宽为 m,
则 ,
矩形菜园面积为 m.
因此,这个矩形的长、宽各为9m时,所用菜园面积最大,最大面积是81㎡.
积有最大值
和为定值
和定积最大
公式变形
① ②
利用基本不等式求最值:
口诀
使用条件
和定积最大,积定和最小
一“正”,二“定”,三“相等”
抽象概括 理论提升
学以致用
根据刚才所学知识,你能解答例2吗?
总结反思
你能谈谈本节课都讲了哪些内容吗?
两个不等式
课堂小结
利用基本不等式求最值
和定积最大
积定和最小
一“正”
二“定”
三“相等”
1.下列说法正确的有 。
A. B.
C. D.
E.
作业布置
2.求下列函数最值
?
?
③
④
一.课本习题3.4 A组2,3,4
二、思考题
谢谢!
统一使用此模版作为PPT展示
封面上请不要标注“xxx学校”
开始说课只需报抽签后的出场代码
这是2002年在北京召开的第24届国际数学家大会会标.会标根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。
走进智者 挑战自我
走进生活 感悟数学
1.知识与技能:学会推导并掌握基本不等式,
理解基本不等式的几何意义,会用基
本不等式求最值、证明不等式;
2.过程和方法:培养观察、试验、归纳、判
断、猜想的思维能力;
3:情感、态度和价值观:敢于探索,体会
数与形的和谐统一,领略数学的应用
价值。
学习目标
A
B
C
D
E
F
G
H
走进智者 挑战自我
自学质疑 交流展示
问题1:正方形边长AB= ,正方形ABCD面积S= .
问题2:四个小三角形的面积和S′为 .
问题3:观察图形,得S S′.
即:
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
A
B
C
D
E(FGH)
形的角度
数的角度
a2+b2-2ab=(a-b)2 0
当 为任意实数时,
都成立吗?
结论:一般地,对于任意实数 ,我们有
当且仅当 时,等号成立.
重要不等式
探究
我们称上述不等式为基本不等式,
其中 叫做 的算术平均数
叫做 的几何平均数
也叫均值不等式.
E
刨根问底 加深理解
观察图:AB是圆O的直径,DE是垂直于直径的弦,其中AC=a,BC=b,讨论下列问题:
讨论
问题1:你能用a、b表示线段OD和DC吗? OD= ,DC= .
问题2:能从图形中得出DC和OD的大小关系吗?
问题3:你能给出基本不等式的的几何解释吗?
几何解释
圆的半径不小于圆内半弦长.
适用范围
文字叙述
“=”成立条件
两数的平方和不小于它们积的2倍
两个正数的算术平均数不小于它们的几何平均数
填表比较:
公式理解
下面说法正确吗?
√
不等式中,不等关
系与字母形式无关
√
√
×
举一反三 学以致用
例1.(1)用篱笆围一个面积为100㎡的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短.最短篱笆是多少?
解 设矩形菜园的长为 m,宽为 m,
则 ,
篱笆长为 m.
因此,这个矩形的长、宽各为10m时,所用篱笆最短.最短篱笆是40m.
积定和最小
积为定值
例1.(2)一个长为36m的篱笆围一个的矩形菜园,问这个矩形的长、宽各为多少时,菜园面积最大.最大面积是多少?
解 设矩形菜园的长为 m,宽为 m,
则 ,
矩形菜园面积为 m.
因此,这个矩形的长、宽各为9m时,所用菜园面积最大,最大面积是81㎡.
积有最大值
和为定值
和定积最大
公式变形
① ②
利用基本不等式求最值:
口诀
使用条件
和定积最大,积定和最小
一“正”,二“定”,三“相等”
抽象概括 理论提升
学以致用
根据刚才所学知识,你能解答例2吗?
总结反思
你能谈谈本节课都讲了哪些内容吗?
两个不等式
课堂小结
利用基本不等式求最值
和定积最大
积定和最小
一“正”
二“定”
三“相等”
1.下列说法正确的有 。
A. B.
C. D.
E.
作业布置
2.求下列函数最值
?
?
③
④
一.课本习题3.4 A组2,3,4
二、思考题
谢谢!
