高中数学人教A版必修二2.3.3-2.3.4线面垂直、面面垂直的性质定理 课件(16张PPT)
文档属性
| 名称 | 高中数学人教A版必修二2.3.3-2.3.4线面垂直、面面垂直的性质定理 课件(16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 630.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 20:57:55 | ||
图片预览




文档简介
2.3.3-2.3.4直线与平面、
平面与平面垂直的性质
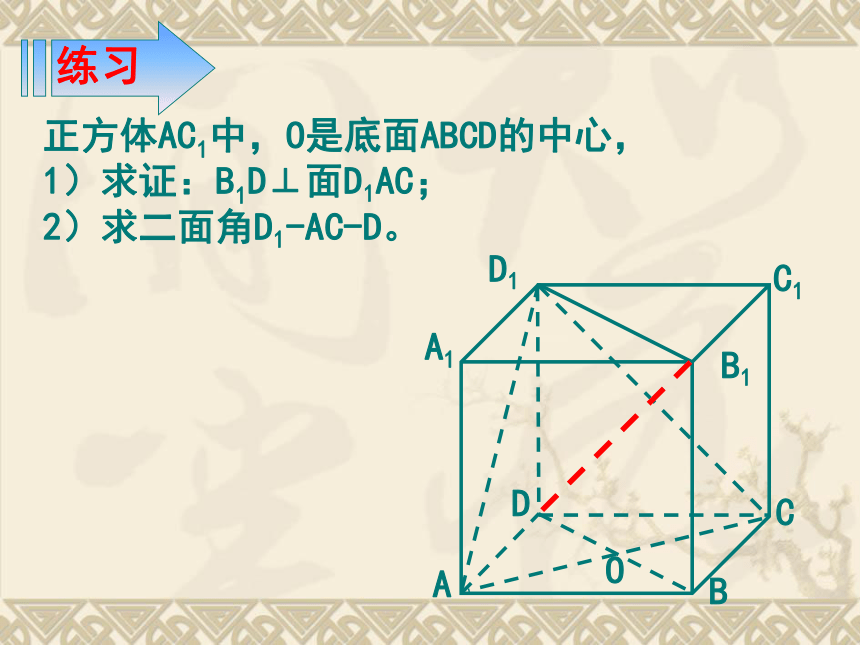
练习
正方体AC1中,O是底面ABCD的中心,
1)求证:B1D⊥面D1AC;
2)求二面角D1-AC-D。
B
C
A
D
D1
C1
B1
A1
O
如果直线 l 与平面 内的任意一条直线都垂直,我们说直线 l 与平面 互相垂直。
直线与平面垂直定义:
线面垂直则线线垂直.
一条直线与一个平面内的两条相交线都垂直,则该直线与此平面垂直.
直线与平面垂直判定定理:
线线垂直则线面垂直.
温故知新
A
B
C
D
α
a
b
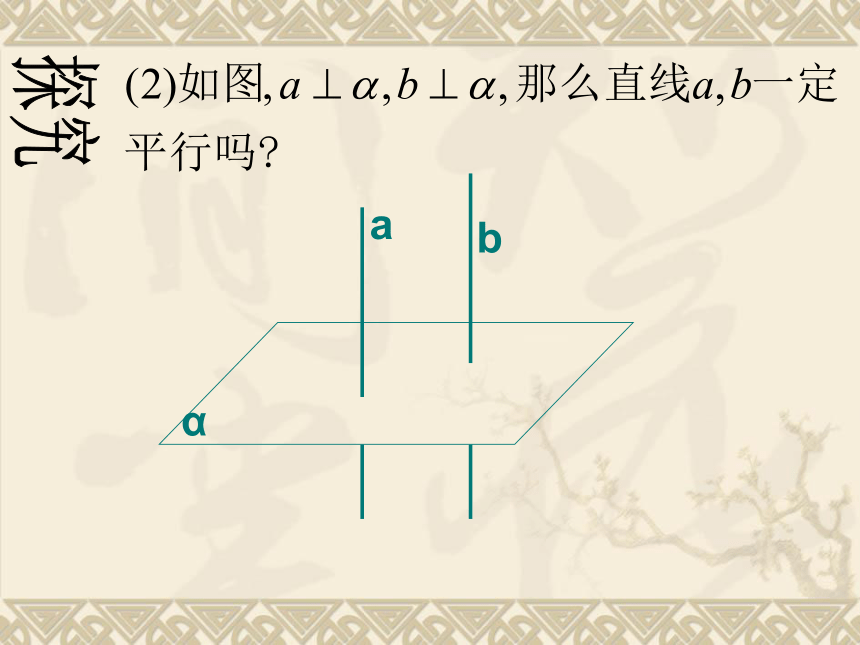
线面垂直的性质定理:
垂直于同一个平面的两条直线平行
α
a
b
o
证明:假设 a与b不平行.
∴b’⊥α.
∴过点o的两条直线 b和b’都垂直平面α,这是不可能的,
b’
1.已知:a⊥α,b⊥α 求证:a//b
记直线b
和α的交点为o,则可过o作 b’∥a
∵a⊥α,
∴a∥b.
反证法
符号语言:
线面垂直
线线平行
简述:
找二面角的平面角
说明该平面角是直角。
面面垂直的判定方法:
1、定义法:
2、判定定理:
(线面垂直?面面垂直)
温故知新
要证两平面垂直,只要在其中一个平面内找到另一个平面的一条垂线。
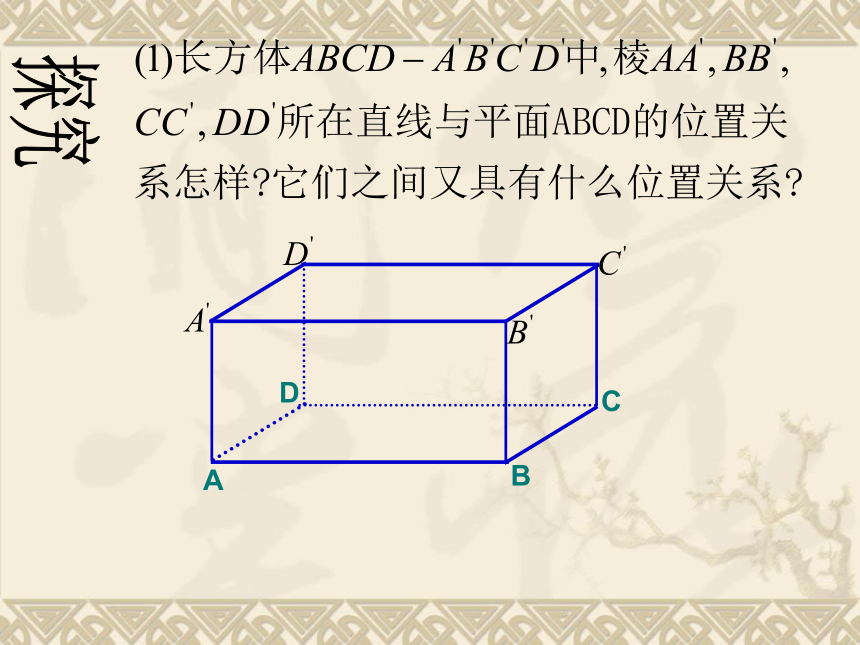
知识探究:
思考1:如果平面α与平面β互相垂直,直线l在平面α内,那么直线l与平面β的位置关系有哪几种可能?
α
β
l
l
α
β
l
α
β
平行
相交
线在面内
知识探究:
思考2:黑板所在平面与地面所在平面垂直,在黑板上是否存在直线与地面垂直?若存在,怎样画线?
α
β
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
面面垂直?线面垂直
α
β
a
A
l
平面与平面垂直的性质定理:
符号语言:
作用:
何时用:已知面面垂直时.
关键:在一个平面内作(找)出垂直于交线的直线.
A
A
推论:两个平面垂直,过其中一个平面内一点作另一个平面的垂线,这条垂线在这个平面内.
α
β
α
β
P
P
例1:如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,
B
O
P
A
C
(2)判断平面PBC与平面PAC的位置关系。
(1)判断BC与平面PAC的位置关系,并证明。
(1)证明:∵ AB是⊙O的直径,C是圆周上不同于A,B的任意一点 ∴∠ACB=90°∴BC⊥AC 又∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BC 平面ABC ∴BC⊥平面PAC
(2)又∵ BC 平面PBC ,∴平面PBC⊥平面PAC
例2:如图,已知PA⊥平面ABC,
平面PAB⊥平面PBC,求证:BC⊥平面PAB
P
A
B
C
E
证明:过点A作AE⊥PB,垂足为E,
∵平面PAB⊥平面PBC,
平面PAB∩平面PBC=PB,
∴AE⊥平面PBC
∵BC 平面PBC ∴AE⊥BC
∵PA⊥平面ABC,BC 平面ABC
∴PA⊥BC
∵PA∩AE=A,∴BC⊥平面PAB
例3
证明:设
b
α
β
a
l
在α内作直线b⊥l
面面垂直性质
线面垂直性质
2、会利用“转化思想”解决垂直问题
线面关系
线线关系
面面关系
线面平行
线线平行
线面垂直
线线垂直
面面垂直
面面平行
课堂小结
1、证题原则:
从已知想性质,从求证想判定
空间问题平面化
注意辅助线的作用
作业: 把直角三角板ABC的直角边BC放置桌面,
另一条直角边AC与桌面所在的平面
垂直,a是
内一条直线,若斜边AB与a垂直,则BC是否与
a垂直?
课本p73 A组2,5 B组4
平面与平面垂直的性质
练习
正方体AC1中,O是底面ABCD的中心,
1)求证:B1D⊥面D1AC;
2)求二面角D1-AC-D。
B
C
A
D
D1
C1
B1
A1
O
如果直线 l 与平面 内的任意一条直线都垂直,我们说直线 l 与平面 互相垂直。
直线与平面垂直定义:
线面垂直则线线垂直.
一条直线与一个平面内的两条相交线都垂直,则该直线与此平面垂直.
直线与平面垂直判定定理:
线线垂直则线面垂直.
温故知新
A
B
C
D
α
a
b
线面垂直的性质定理:
垂直于同一个平面的两条直线平行
α
a
b
o
证明:假设 a与b不平行.
∴b’⊥α.
∴过点o的两条直线 b和b’都垂直平面α,这是不可能的,
b’
1.已知:a⊥α,b⊥α 求证:a//b
记直线b
和α的交点为o,则可过o作 b’∥a
∵a⊥α,
∴a∥b.
反证法
符号语言:
线面垂直
线线平行
简述:
找二面角的平面角
说明该平面角是直角。
面面垂直的判定方法:
1、定义法:
2、判定定理:
(线面垂直?面面垂直)
温故知新
要证两平面垂直,只要在其中一个平面内找到另一个平面的一条垂线。
知识探究:
思考1:如果平面α与平面β互相垂直,直线l在平面α内,那么直线l与平面β的位置关系有哪几种可能?
α
β
l
l
α
β
l
α
β
平行
相交
线在面内
知识探究:
思考2:黑板所在平面与地面所在平面垂直,在黑板上是否存在直线与地面垂直?若存在,怎样画线?
α
β
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
面面垂直?线面垂直
α
β
a
A
l
平面与平面垂直的性质定理:
符号语言:
作用:
何时用:已知面面垂直时.
关键:在一个平面内作(找)出垂直于交线的直线.
A
A
推论:两个平面垂直,过其中一个平面内一点作另一个平面的垂线,这条垂线在这个平面内.
α
β
α
β
P
P
例1:如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,
B
O
P
A
C
(2)判断平面PBC与平面PAC的位置关系。
(1)判断BC与平面PAC的位置关系,并证明。
(1)证明:∵ AB是⊙O的直径,C是圆周上不同于A,B的任意一点 ∴∠ACB=90°∴BC⊥AC 又∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BC 平面ABC ∴BC⊥平面PAC
(2)又∵ BC 平面PBC ,∴平面PBC⊥平面PAC
例2:如图,已知PA⊥平面ABC,
平面PAB⊥平面PBC,求证:BC⊥平面PAB
P
A
B
C
E
证明:过点A作AE⊥PB,垂足为E,
∵平面PAB⊥平面PBC,
平面PAB∩平面PBC=PB,
∴AE⊥平面PBC
∵BC 平面PBC ∴AE⊥BC
∵PA⊥平面ABC,BC 平面ABC
∴PA⊥BC
∵PA∩AE=A,∴BC⊥平面PAB
例3
证明:设
b
α
β
a
l
在α内作直线b⊥l
面面垂直性质
线面垂直性质
2、会利用“转化思想”解决垂直问题
线面关系
线线关系
面面关系
线面平行
线线平行
线面垂直
线线垂直
面面垂直
面面平行
课堂小结
1、证题原则:
从已知想性质,从求证想判定
空间问题平面化
注意辅助线的作用
作业: 把直角三角板ABC的直角边BC放置桌面,
另一条直角边AC与桌面所在的平面
垂直,a是
内一条直线,若斜边AB与a垂直,则BC是否与
a垂直?
课本p73 A组2,5 B组4
