人教A版高中数学必修1第三章3.2.1 几类不同增长的函数模型课件 (1)(24张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第三章3.2.1 几类不同增长的函数模型课件 (1)(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 328.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 21:52:05 | ||
图片预览





文档简介
3.2.1 几类不同增长的函数模型
第二课时
幂、指、对函数模型的
差异性
问题提出
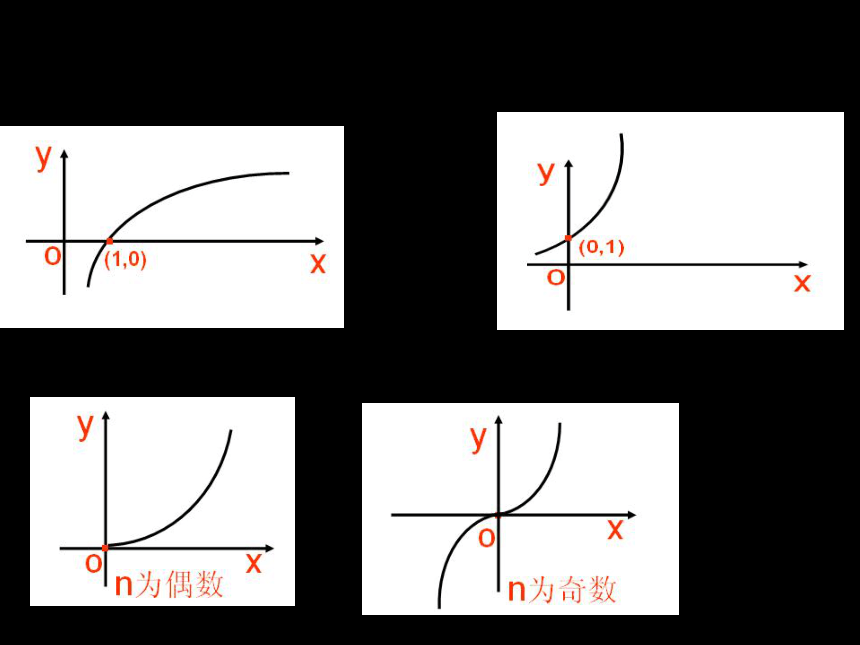
1.指数函数y=ax (a>1),对数函数 y=logax(a>1)和幂函数y=x n (n>0)在区间(0,+∞)上的单调性如何?
问题提出
2.利用这三类函数模型解决实际问题,其增长速度是有差异的,我们怎样认识这种差异呢?
探究(一):特殊幂、指、对函数模型的差异
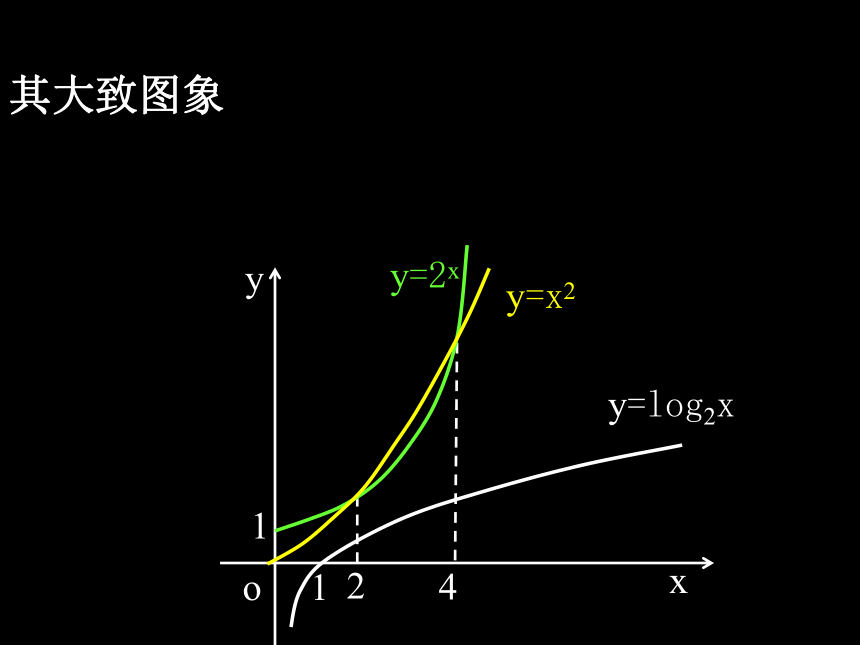
对于函数模型 :y=2x, y=x2, y=log2x 其中x>0.
思考1:观察三个函数的自变量与函数值对应 表, 这三个函数增长的快慢情况如何?
…
1.766
1.585
1.379
1.138
0.848
0.485
0
-0.737
-2.322
y=log2x
…
11.56
9
6.76
4.84
3.24
1.96
1
0.36
0.04
y=x2
…
10.556
8
6.063
4.595
3.482
2.639
2
1.516
1.149
y=2x
…
3.4
3.0
2.6
2.2
1.8
1.4
1
0.6
0.2
x
其大致图象
x
y
o
1
1
2
4
y=2x
y=x2
y=log2x
x
0
1
2
3
4
5
6
7
8
y=2x
1
2
4
8
16
32
64
128
256
y=x2
0
1
4
9
16
25
36
49
64
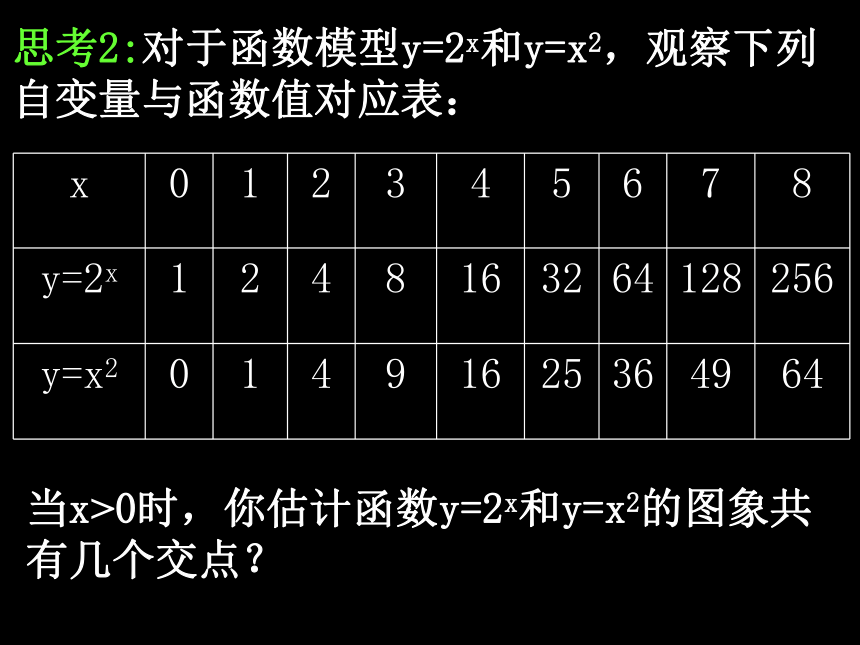
思考2:对于函数模型y=2x和y=x2,观察下列自变量与函数值对应表:
当x>0时,你估计函数y=2x和y=x2的图象共有几个交点?
其大致图象
x
y
o
1
1
2
4
y=2x
y=x2
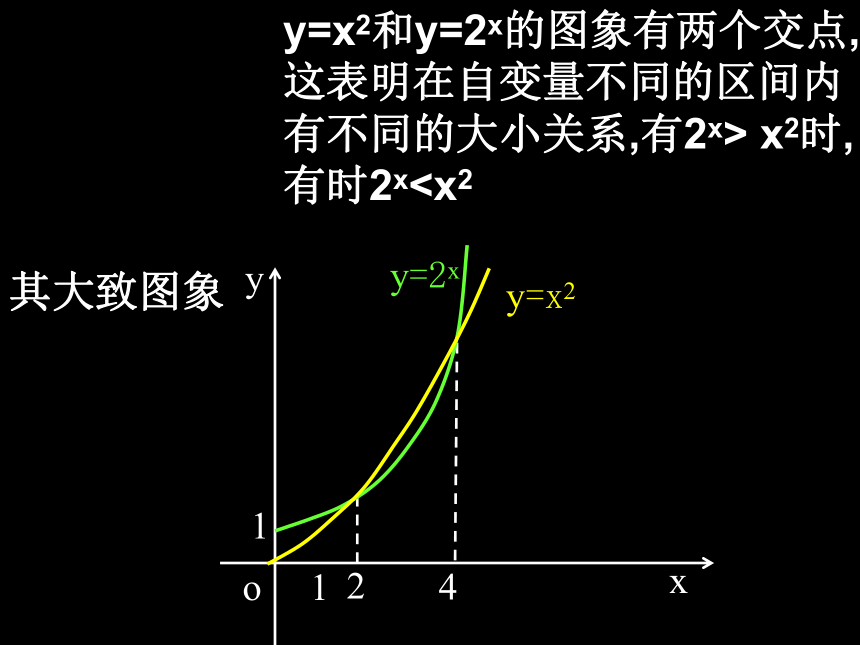
y=x2和y=2x的图象有两个交点,这表明在自变量不同的区间内有不同的大小关系,有2x> x2时,有时2x x
0
10
20
30
40
50
60
70
80
1
1024
1.05
E+06
1.07
E+09
1.10
E+12
1.13
E+15
1.15
E+18
1.18
E+21
1.21
E+24
0
100
400
900
1600
2500
3600
4900
6400
…
…
…
1.10E+12
1.13E+15
50
100
y
x
0
探究(二):一般幂、指、对函数模型的差异
思考1:对任意给定的a>1和n>0,在区间
(0,+∞)上ax是否恒大于或恒小于xn?
思考2:当a>1,n>0时,在区间(0,+∞)上,
ax与xn的大小关系应如何阐述?
结论
一般地,对于指数函数 和幂函数
通过探索可以发现,在区间(0,+∞)上,无论n比a大多少,尽管在x的一定变化范围内, 会小于 ,
但由于 的增长快于 的增长,因此,总存在一个 ,当 时,就会有
x
y
o
1
1
2
4
y=2x
y=x2
观察图象:对y=x2和y=log2x的增长情况进行比较
x
y
o
1
1
2
4
y=x2
y=log2x
思考3:对任意给定的a>1和n>0,在区间 (0,+∞)上,logax是否恒大于或恒小于xn?
思考4:随着x的增大,logax增长速度的快慢程度如何变化? xn增长速度的快慢程度如何变化?
x
y
o
1
y=xn
y=logax
x
y
o
1
y=logax
y=xn
思考5:当x充分大时,logax(a>1)与xn(n>0)谁的增长速度相对较快?
x
y
o
1
y=logax
y=xn
同样地,对于对数函数 和幂函数
,在区间(0,+∞)上,随着x的增大,
增长得越来越慢,图象就像是渐渐地与x轴平行一样,尽管在x的一定变化范围内, 可能会大于 ,但由于 的增长慢于 的增长,因此,总存在一个 ,当 时,就会有
结论
根据图象,不等式log2x<2xlog2xx
y
o
1
1
2
4
y=2x
y=x2
y=log2x
思考6:对于指数函数y=ax(a>1),对数函数 y=logax(a>1)和幂函数y=xn(n>0),总存在一个x0,使x>x0时,ax,logax,xn三者的大小关系如何?
综上所述
在区间(0,+∞)上,尽管 , 和 都是增函数,但它们的增长速度不同,而且不在同一个"档次"上,随着x的增大, 的增长速度越来越快,会超过并远远大于的 增长速度,而
的增长速度则越来越慢.因此,总会存在一个 ,当 时,就有
思考7:指数函数y=ax (0x
y
o
1
y=ax
y=xn
y=logax
本课小结
提出问题:
1.今天我们主要学习了什么新的知识?
2.有什么办法可能用来研究不同函数的增长情况?
3.研究一个新的数学问题,想推导一般性结论,我们是怎么样做的?
谢谢大家
再 见!
第二课时
幂、指、对函数模型的
差异性
问题提出
1.指数函数y=ax (a>1),对数函数 y=logax(a>1)和幂函数y=x n (n>0)在区间(0,+∞)上的单调性如何?
问题提出
2.利用这三类函数模型解决实际问题,其增长速度是有差异的,我们怎样认识这种差异呢?
探究(一):特殊幂、指、对函数模型的差异
对于函数模型 :y=2x, y=x2, y=log2x 其中x>0.
思考1:观察三个函数的自变量与函数值对应 表, 这三个函数增长的快慢情况如何?
…
1.766
1.585
1.379
1.138
0.848
0.485
0
-0.737
-2.322
y=log2x
…
11.56
9
6.76
4.84
3.24
1.96
1
0.36
0.04
y=x2
…
10.556
8
6.063
4.595
3.482
2.639
2
1.516
1.149
y=2x
…
3.4
3.0
2.6
2.2
1.8
1.4
1
0.6
0.2
x
其大致图象
x
y
o
1
1
2
4
y=2x
y=x2
y=log2x
x
0
1
2
3
4
5
6
7
8
y=2x
1
2
4
8
16
32
64
128
256
y=x2
0
1
4
9
16
25
36
49
64
思考2:对于函数模型y=2x和y=x2,观察下列自变量与函数值对应表:
当x>0时,你估计函数y=2x和y=x2的图象共有几个交点?
其大致图象
x
y
o
1
1
2
4
y=2x
y=x2
y=x2和y=2x的图象有两个交点,这表明在自变量不同的区间内有不同的大小关系,有2x> x2时,有时2x
0
10
20
30
40
50
60
70
80
1
1024
1.05
E+06
1.07
E+09
1.10
E+12
1.13
E+15
1.15
E+18
1.18
E+21
1.21
E+24
0
100
400
900
1600
2500
3600
4900
6400
…
…
…
1.10E+12
1.13E+15
50
100
y
x
0
探究(二):一般幂、指、对函数模型的差异
思考1:对任意给定的a>1和n>0,在区间
(0,+∞)上ax是否恒大于或恒小于xn?
思考2:当a>1,n>0时,在区间(0,+∞)上,
ax与xn的大小关系应如何阐述?
结论
一般地,对于指数函数 和幂函数
通过探索可以发现,在区间(0,+∞)上,无论n比a大多少,尽管在x的一定变化范围内, 会小于 ,
但由于 的增长快于 的增长,因此,总存在一个 ,当 时,就会有
x
y
o
1
1
2
4
y=2x
y=x2
观察图象:对y=x2和y=log2x的增长情况进行比较
x
y
o
1
1
2
4
y=x2
y=log2x
思考3:对任意给定的a>1和n>0,在区间 (0,+∞)上,logax是否恒大于或恒小于xn?
思考4:随着x的增大,logax增长速度的快慢程度如何变化? xn增长速度的快慢程度如何变化?
x
y
o
1
y=xn
y=logax
x
y
o
1
y=logax
y=xn
思考5:当x充分大时,logax(a>1)与xn(n>0)谁的增长速度相对较快?
x
y
o
1
y=logax
y=xn
同样地,对于对数函数 和幂函数
,在区间(0,+∞)上,随着x的增大,
增长得越来越慢,图象就像是渐渐地与x轴平行一样,尽管在x的一定变化范围内, 可能会大于 ,但由于 的增长慢于 的增长,因此,总存在一个 ,当 时,就会有
结论
根据图象,不等式log2x<2x
y
o
1
1
2
4
y=2x
y=x2
y=log2x
思考6:对于指数函数y=ax(a>1),对数函数 y=logax(a>1)和幂函数y=xn(n>0),总存在一个x0,使x>x0时,ax,logax,xn三者的大小关系如何?
综上所述
在区间(0,+∞)上,尽管 , 和 都是增函数,但它们的增长速度不同,而且不在同一个"档次"上,随着x的增大, 的增长速度越来越快,会超过并远远大于的 增长速度,而
的增长速度则越来越慢.因此,总会存在一个 ,当 时,就有
思考7:指数函数y=ax (0
y
o
1
y=ax
y=xn
y=logax
本课小结
提出问题:
1.今天我们主要学习了什么新的知识?
2.有什么办法可能用来研究不同函数的增长情况?
3.研究一个新的数学问题,想推导一般性结论,我们是怎么样做的?
谢谢大家
再 见!
