人教A版高中数学必修1第三章3.2.1 几类不同增长的函数模型课件 (2)(15张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第三章3.2.1 几类不同增长的函数模型课件 (2)(15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 223.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 21:55:36 | ||
图片预览






文档简介
3.2.1几类不同增长的函数模型(一)
例1.假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问:你会选择哪种投资方案?
选择投资方案的标准?
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
思考:各方案每天回报的变化情况可用什么函数模型去刻画?
y=40(x∈N*)
y=10x(x∈N*)
y=0.4×2x-1 (x∈N*)
解:设第x天所得回报为y元,则
x/天
方案一
方案二
方案三
y/元
增量/元
y/元
增量/元
y/元
增量/元
1
40
10
0.4
2
40
20
0.8
3
40
30
1.6
4
40
5
40
6
40
7
40
8
40
9
40
…
…
…
…
30
40
300
214748364.8
40
50
60
70
80
90
3.2
6.4
12.8
25.6
51.2
102.4
列表法比较三种方案的日回报量
0
0
0
0
0
0
0
0
…
0
10
10
10
10
10
10
10
10
…
10
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
…
107374182.4
1
2
3
4
6
5
7
8
9
10
20
0
40
60
80
100
120
140
y
x
方案一:y=40
1
2
3
4
5
6
7
8
9
10
…
40
40
40
40
40
40
40
40
40
40
…
x
方案二
y=10x
1
2
3
4
5
6
7
8
9
10
…
10
20
30
40
50
60
70
80
90
100
…
x
y=0.4*2x-1
1
2
3
4
5
6
7
8
9
10
…
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
204.8
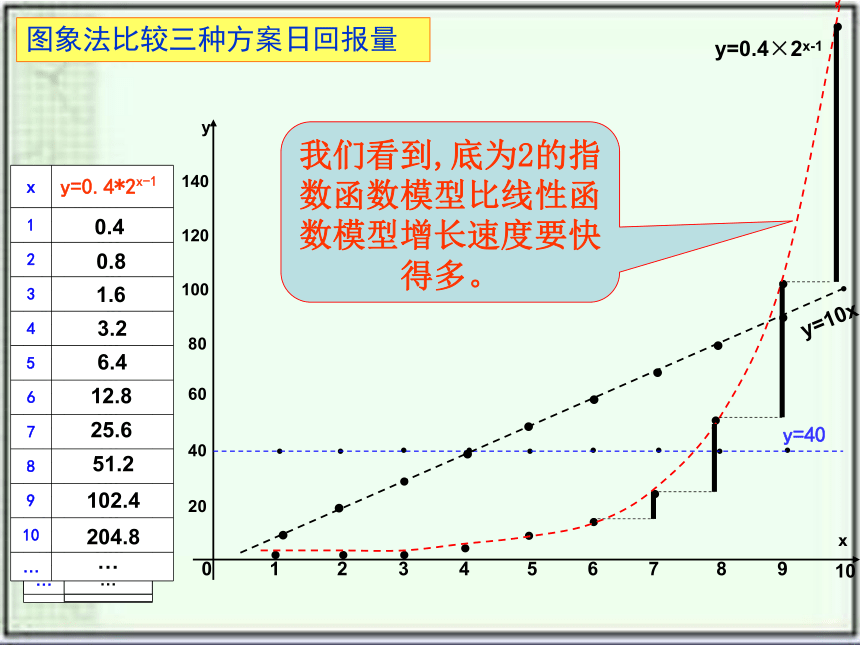
图象法比较三种方案日回报量
y=40
y=10x
y=0.4×2x-1
x
…
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多。
累计回报表
天数
方案
1
2
3
4
5
6
7
8
9
10
11
一
二
三
40
80
120
160
200
240
280
320
360
400
440
10
30
60
100
150
210
280
360
450
550
660
0.4
1.2
2.8
6
12.4
25.2
50.8
102
204.4
409.2
816.8
投资__________ 应选择第一种投资方案;
投资___________应选择第二种投资方案;
投资____________________应选择第三种投资方案。
11天(含11天)以上,
8~10天,
1~7天,
列表法比较三种方案的累计回报
四个变量 随变量 变化的数据如下表:
1.005
1.0151
1.0461
1.1407
1.4295
2.3107
5
155
130
105
80
55
30
5
33733
1785.2
94.478
5
4505
3130
2005
1130
505
130
5
30
25
20
15
10
5
0
关于x呈指数型函数变化的
变量是
练习一
练习二
2.某种计算机病毒是通过电子邮件进行传播的,如果某台计算机感染上这种病毒,那么每轮病毒发作时,这台计算机都可能感染没被感染的20台计算机.现在10台计算机在第1轮病毒发作时被感染,问在第5轮病毒发作时可能有多少台计算机被感染?
第一轮
第二轮
第三轮
第四轮
第五轮
被感染的电脑数量
10
常数函数
一次函数
指数型函数
几种常见函数的增长情况:
保持不变
直线上升
匀速增长
急剧增长
指数爆炸
没有增长
例2、公司为了实现1000万元利润的目标,准备制定了一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:
y=0.25x, y=log7x+1, y=1.002x ,
其中哪个模型能符合公司的要求?
一次函数
对数型函数
指数函数
(1)例2涉及了哪几类函数模型?
分析:
①销售利润达到10万元时,按销售利润进行奖励,且人员销售利润一般不会超过公司总的利润1000万元,所以销售利润x可用不等式表示为____________.
③依据这个模型进行奖励时,奖金不超过利润的25%,所以奖金y可用不等式表示______________.
②依据这个模型进行奖励时,奖金总数不超过5万元,所以奖金y可用不等式表示为__________.
(2)你能用数学语言描述符合公司奖励方案条件吗?
通过观察函数图象得到初步结论:按对数模型进行奖励时符合公司的要求。
400
600
800
1000
1200
200
1
2
3
4
5
6
7
8
x
y
o
对数增长模型比较适合于描述增长速度平缓的变化规律。
y=5
y=0.25x
下面列表计算确认上述判断:
x
y
o
2.5
1.02
2.18
5
1.04
2.54
…
…
…
4.95
4.44
5.04
4.442
…
…
…
4.55
模型
奖金/万元
利润
10
20
800
810
1000
…
…
y=0.25X
我们来看函数 的图象:
7
综上所述:模型 确实符合公司要求.
1
log
+
=
x
y
问题:当 时,奖金是否不超过利润的25%呢?
10
1. 几类不同增长的函数模型(一次函数、指数函数、对数函数)的差异。
2. 几类增长函数建模的步骤
列解析式
具体问题
画出图像(形)
列出表格(数)
不同增长
确定模型
预报和决策
控制和优化
小结
常数函数
一次函数
指数函数
对数函数
增长量为零
增长量相同
增长量迅速增加
增长量减少
没有增长
直线增长
指数爆炸
对数缓慢增长
再见!
例1.假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问:你会选择哪种投资方案?
选择投资方案的标准?
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
思考:各方案每天回报的变化情况可用什么函数模型去刻画?
y=40(x∈N*)
y=10x(x∈N*)
y=0.4×2x-1 (x∈N*)
解:设第x天所得回报为y元,则
x/天
方案一
方案二
方案三
y/元
增量/元
y/元
增量/元
y/元
增量/元
1
40
10
0.4
2
40
20
0.8
3
40
30
1.6
4
40
5
40
6
40
7
40
8
40
9
40
…
…
…
…
30
40
300
214748364.8
40
50
60
70
80
90
3.2
6.4
12.8
25.6
51.2
102.4
列表法比较三种方案的日回报量
0
0
0
0
0
0
0
0
…
0
10
10
10
10
10
10
10
10
…
10
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
…
107374182.4
1
2
3
4
6
5
7
8
9
10
20
0
40
60
80
100
120
140
y
x
方案一:y=40
1
2
3
4
5
6
7
8
9
10
…
40
40
40
40
40
40
40
40
40
40
…
x
方案二
y=10x
1
2
3
4
5
6
7
8
9
10
…
10
20
30
40
50
60
70
80
90
100
…
x
y=0.4*2x-1
1
2
3
4
5
6
7
8
9
10
…
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
204.8
图象法比较三种方案日回报量
y=40
y=10x
y=0.4×2x-1
x
…
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多。
累计回报表
天数
方案
1
2
3
4
5
6
7
8
9
10
11
一
二
三
40
80
120
160
200
240
280
320
360
400
440
10
30
60
100
150
210
280
360
450
550
660
0.4
1.2
2.8
6
12.4
25.2
50.8
102
204.4
409.2
816.8
投资__________ 应选择第一种投资方案;
投资___________应选择第二种投资方案;
投资____________________应选择第三种投资方案。
11天(含11天)以上,
8~10天,
1~7天,
列表法比较三种方案的累计回报
四个变量 随变量 变化的数据如下表:
1.005
1.0151
1.0461
1.1407
1.4295
2.3107
5
155
130
105
80
55
30
5
33733
1785.2
94.478
5
4505
3130
2005
1130
505
130
5
30
25
20
15
10
5
0
关于x呈指数型函数变化的
变量是
练习一
练习二
2.某种计算机病毒是通过电子邮件进行传播的,如果某台计算机感染上这种病毒,那么每轮病毒发作时,这台计算机都可能感染没被感染的20台计算机.现在10台计算机在第1轮病毒发作时被感染,问在第5轮病毒发作时可能有多少台计算机被感染?
第一轮
第二轮
第三轮
第四轮
第五轮
被感染的电脑数量
10
常数函数
一次函数
指数型函数
几种常见函数的增长情况:
保持不变
直线上升
匀速增长
急剧增长
指数爆炸
没有增长
例2、公司为了实现1000万元利润的目标,准备制定了一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:
y=0.25x, y=log7x+1, y=1.002x ,
其中哪个模型能符合公司的要求?
一次函数
对数型函数
指数函数
(1)例2涉及了哪几类函数模型?
分析:
①销售利润达到10万元时,按销售利润进行奖励,且人员销售利润一般不会超过公司总的利润1000万元,所以销售利润x可用不等式表示为____________.
③依据这个模型进行奖励时,奖金不超过利润的25%,所以奖金y可用不等式表示______________.
②依据这个模型进行奖励时,奖金总数不超过5万元,所以奖金y可用不等式表示为__________.
(2)你能用数学语言描述符合公司奖励方案条件吗?
通过观察函数图象得到初步结论:按对数模型进行奖励时符合公司的要求。
400
600
800
1000
1200
200
1
2
3
4
5
6
7
8
x
y
o
对数增长模型比较适合于描述增长速度平缓的变化规律。
y=5
y=0.25x
下面列表计算确认上述判断:
x
y
o
2.5
1.02
2.18
5
1.04
2.54
…
…
…
4.95
4.44
5.04
4.442
…
…
…
4.55
模型
奖金/万元
利润
10
20
800
810
1000
…
…
y=0.25X
我们来看函数 的图象:
7
综上所述:模型 确实符合公司要求.
1
log
+
=
x
y
问题:当 时,奖金是否不超过利润的25%呢?
10
1. 几类不同增长的函数模型(一次函数、指数函数、对数函数)的差异。
2. 几类增长函数建模的步骤
列解析式
具体问题
画出图像(形)
列出表格(数)
不同增长
确定模型
预报和决策
控制和优化
小结
常数函数
一次函数
指数函数
对数函数
增长量为零
增长量相同
增长量迅速增加
增长量减少
没有增长
直线增长
指数爆炸
对数缓慢增长
再见!
