人教A版高中数学必修1第三章3.2.1 几类不同增长的函数模型课件 (3)(15张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第三章3.2.1 几类不同增长的函数模型课件 (3)(15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 21:57:32 | ||
图片预览






文档简介
生态故事:“一群兔子引发的危机”
1859年,当澳大利亚的一个农夫为了打猎而从外国弄来几只兔子后,一场可怕的生态灾难爆发了。兔子是出了名的快速繁殖者,在澳大利亚它没有天敌,数量不断翻番。1950年,澳大利亚的兔子的数量从最初的五只增加到了五亿只,这个
国家绝大部分地区的庄稼或草地
都遭到了极大损失。绝望之中,
人们从巴西引入了多发黏液瘤病
,以对付迅速繁殖的兔子。整个
20世纪中期,澳大利亚的灭兔行
动从未停止过。
“指数爆炸”
例1.小明今年大学刚毕业,找工作四处碰壁,父母考虑再三,最后决定筹措一笔资金给小明用于投资,现有三种投资方案供其选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回
报10元;
方案三:第一天回报0.4元,以后每天回报比前一天
翻一番.
请问:小明应该选择哪种投资方案?
投资方案选择原则:
⑴比较三种方案每天回报数;
⑵比较三种方案一段时间内的累计回报数.
投入资金相同,回报数多者为优.
方法:
三种投资方案在前30天的日回报情况
方案一
日回报数
方案二
日回报数
方案三
日回报数
1
2
3
4
5
6
7
8
9
10
...
30
40
40
40
40
40
40
40
40
40
40
10
20
30
40
60
70
90
100
204.8
解:
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
80
50
40
300
214748364.8
...
...
...
累计回报表
一
二
三
1
2
3
4
5
6
7
8
9
10
11
12
方案
回报/元
天数
40
80
120
160
200
240
280
10
60
102
204.4
409.2
818.8
1638
320
360
400
440
480
30
100
150
210
280
360
450
550
660
780
0.4
1.2
2.8
6
12.4
25.2
50.8
方案一
方案一
方案二
方案一
方案三
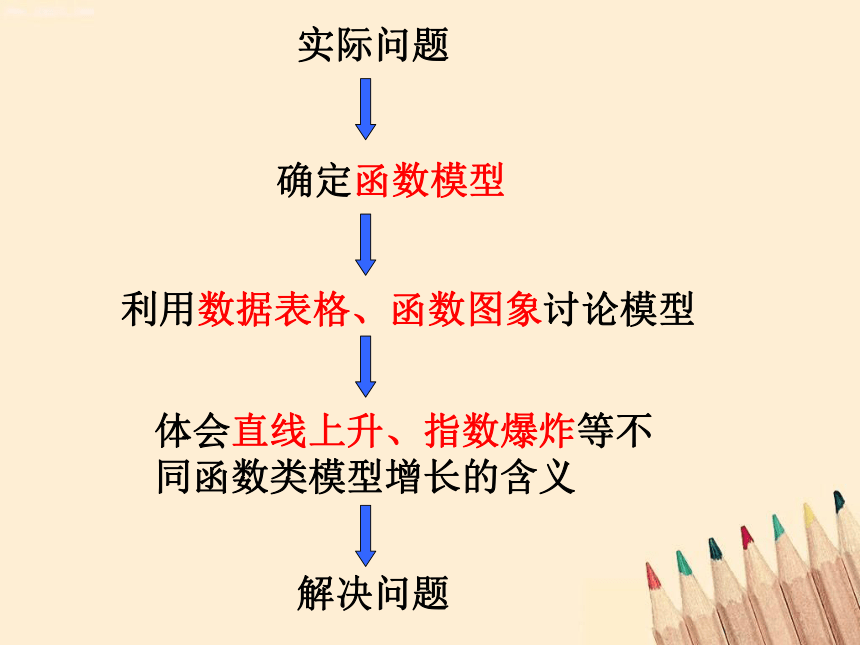
确定函数模型
利用数据表格、函数图象讨论模型
体会直线上升、指数爆炸等不
同函数类模型增长的含义
实际问题
解决问题
生态故事:“一群兔子引发的危机”
1859年,当澳大利亚的一个农夫为了打猎而从外国弄来几只兔子后,一场可怕的生态灾难爆发了。兔子是出了名的快速繁殖者,在澳大利亚它没有天敌,数量不断翻番。1950年,澳大利亚的兔子的数量从最初的五只增加到了五亿只,这个
国家绝大部分地区的庄稼或草地
都遭到了极大损失。绝望之中,
人们从巴西引入了多发黏液瘤病
,以对付迅速繁殖的兔子。整个
20世纪中期,澳大利亚的灭兔行
动从未停止过。
“指数爆炸”
例2.假设小明投资后为了实现1000万元利润的目标,
准备制定一个激励销售人员的奖励方案:
在销售利润达到10万元时,按销售利润进行奖励,且奖金 (单位:万元)随销售利润 (单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%。
现有三个奖励模型:
其中那个模型能符合公司的要求?
思考:你能用数学语言描述符合公司奖励方案的要求吗?
⑴销售利润达到10万元时进行奖励;
⑵奖金总数不超过5万元;
⑶奖金不超过利润的25%;
注:公司总的利润目标为1000万元.
三个奖励模型的函数值表
1
0.25
1.00
1.00
100
25
3.37
1.22
200
50
3.72
1.49
300
75
3.93
1.82
400
100
4.08
2.22
500
125
4.19
2.72
600
150
4.29
3.32
700
175
4.37
4.05
800
200
4.44
4.95
900
225
4.50
6.04
1000
250
4.55
7.37
首先计算哪个模型的奖金
总数不超过5万元.
因此当 时,
解:
⑴对于模型 ,
它在区间
上递增,
当 时,
所以该模型
,
不符合要求;
,
⑵对于模型 ,
由函数
图象,
并利用计算器,
可知在区间
内有一个点 满足
由于它在区间
,
上递增,
因此当 时,
,
所以该模型也不符合要求;
⑶对于模型 ,
它在区间 上递增,
且
时,
所以它符合奖金总数
不超过五万的要求.
,
思考:
问题即为:
是否满足要求“奖金不超过利润的25%”?
解:
利用计算机作出函数
由图象可知它是递减的,
因此
即
所以,
说明按模型 奖励,奖金不会超过利润的25% .
综上所述,模型 确实能符合公司要求.
的图象,
课堂小结:
通过实例,体验建立数学模型的过程,利用表格、作图体会和认识直线上升、指数爆炸、对数增长等不同函数模型的增长的含义,认识数学的价值,认识数学与现实生活、其他学科的密切联系,从而体会数学的实用价值,享受数学的应用美.
课后作业:
1.教材98页练习2;
2.教材107页习题3.2 A组1、2.
方案一
方案二
方案三
1
2
3
4
5
6
7
8
9
10
30
增加量/元
增加量/元
增加量/元
40
0
0
0
0
0
0
0
0
0
...
0
10
20
30
40
50
60
70
80
90
100
300
...
10
10
10
10
10
10
10
10
10
10
...
...
...
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
204.8
214748364.8
0.4
0.8
1.6
3.2
6.4
102.4
25.6
12.8
51.2
107374182.4
40
...
40
40
40
40
40
40
40
40
40
...
0
1859年,当澳大利亚的一个农夫为了打猎而从外国弄来几只兔子后,一场可怕的生态灾难爆发了。兔子是出了名的快速繁殖者,在澳大利亚它没有天敌,数量不断翻番。1950年,澳大利亚的兔子的数量从最初的五只增加到了五亿只,这个
国家绝大部分地区的庄稼或草地
都遭到了极大损失。绝望之中,
人们从巴西引入了多发黏液瘤病
,以对付迅速繁殖的兔子。整个
20世纪中期,澳大利亚的灭兔行
动从未停止过。
“指数爆炸”
例1.小明今年大学刚毕业,找工作四处碰壁,父母考虑再三,最后决定筹措一笔资金给小明用于投资,现有三种投资方案供其选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回
报10元;
方案三:第一天回报0.4元,以后每天回报比前一天
翻一番.
请问:小明应该选择哪种投资方案?
投资方案选择原则:
⑴比较三种方案每天回报数;
⑵比较三种方案一段时间内的累计回报数.
投入资金相同,回报数多者为优.
方法:
三种投资方案在前30天的日回报情况
方案一
日回报数
方案二
日回报数
方案三
日回报数
1
2
3
4
5
6
7
8
9
10
...
30
40
40
40
40
40
40
40
40
40
40
10
20
30
40
60
70
90
100
204.8
解:
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
80
50
40
300
214748364.8
...
...
...
累计回报表
一
二
三
1
2
3
4
5
6
7
8
9
10
11
12
方案
回报/元
天数
40
80
120
160
200
240
280
10
60
102
204.4
409.2
818.8
1638
320
360
400
440
480
30
100
150
210
280
360
450
550
660
780
0.4
1.2
2.8
6
12.4
25.2
50.8
方案一
方案一
方案二
方案一
方案三
确定函数模型
利用数据表格、函数图象讨论模型
体会直线上升、指数爆炸等不
同函数类模型增长的含义
实际问题
解决问题
生态故事:“一群兔子引发的危机”
1859年,当澳大利亚的一个农夫为了打猎而从外国弄来几只兔子后,一场可怕的生态灾难爆发了。兔子是出了名的快速繁殖者,在澳大利亚它没有天敌,数量不断翻番。1950年,澳大利亚的兔子的数量从最初的五只增加到了五亿只,这个
国家绝大部分地区的庄稼或草地
都遭到了极大损失。绝望之中,
人们从巴西引入了多发黏液瘤病
,以对付迅速繁殖的兔子。整个
20世纪中期,澳大利亚的灭兔行
动从未停止过。
“指数爆炸”
例2.假设小明投资后为了实现1000万元利润的目标,
准备制定一个激励销售人员的奖励方案:
在销售利润达到10万元时,按销售利润进行奖励,且奖金 (单位:万元)随销售利润 (单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%。
现有三个奖励模型:
其中那个模型能符合公司的要求?
思考:你能用数学语言描述符合公司奖励方案的要求吗?
⑴销售利润达到10万元时进行奖励;
⑵奖金总数不超过5万元;
⑶奖金不超过利润的25%;
注:公司总的利润目标为1000万元.
三个奖励模型的函数值表
1
0.25
1.00
1.00
100
25
3.37
1.22
200
50
3.72
1.49
300
75
3.93
1.82
400
100
4.08
2.22
500
125
4.19
2.72
600
150
4.29
3.32
700
175
4.37
4.05
800
200
4.44
4.95
900
225
4.50
6.04
1000
250
4.55
7.37
首先计算哪个模型的奖金
总数不超过5万元.
因此当 时,
解:
⑴对于模型 ,
它在区间
上递增,
当 时,
所以该模型
,
不符合要求;
,
⑵对于模型 ,
由函数
图象,
并利用计算器,
可知在区间
内有一个点 满足
由于它在区间
,
上递增,
因此当 时,
,
所以该模型也不符合要求;
⑶对于模型 ,
它在区间 上递增,
且
时,
所以它符合奖金总数
不超过五万的要求.
,
思考:
问题即为:
是否满足要求“奖金不超过利润的25%”?
解:
利用计算机作出函数
由图象可知它是递减的,
因此
即
所以,
说明按模型 奖励,奖金不会超过利润的25% .
综上所述,模型 确实能符合公司要求.
的图象,
课堂小结:
通过实例,体验建立数学模型的过程,利用表格、作图体会和认识直线上升、指数爆炸、对数增长等不同函数模型的增长的含义,认识数学的价值,认识数学与现实生活、其他学科的密切联系,从而体会数学的实用价值,享受数学的应用美.
课后作业:
1.教材98页练习2;
2.教材107页习题3.2 A组1、2.
方案一
方案二
方案三
1
2
3
4
5
6
7
8
9
10
30
增加量/元
增加量/元
增加量/元
40
0
0
0
0
0
0
0
0
0
...
0
10
20
30
40
50
60
70
80
90
100
300
...
10
10
10
10
10
10
10
10
10
10
...
...
...
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
204.8
214748364.8
0.4
0.8
1.6
3.2
6.4
102.4
25.6
12.8
51.2
107374182.4
40
...
40
40
40
40
40
40
40
40
40
...
0
