人教A版高中数学必修1第三章3.2.1 几类不同增长的函数模型课件 (6)(20张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第三章3.2.1 几类不同增长的函数模型课件 (6)(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 22:21:55 | ||
图片预览





文档简介
3.2.1几类不同增长的函数模型(一)
课 堂 引 入
思考:在生活中,你能举出增长的例子吗?
函数是描述客观世界变化规律的基本数学模型不同的增长规律需要不同的函数模型来描述的,我们学过的函数模型有哪些呢?
一次函数,二次函数,指数函数,对数函数,幂函数等等
对于实际问题,我们如何选择一个恰当的函数模型来刻画它呢?
找出模型后又是如何去研究它的增长规律呢?
例1.假如你有一笔资金用于投资,现有三种方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元以后每天比前一天多10元
方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。
请问,你会选择哪种投资方案?
提 出 问 题
问题1:你会选择什么样的回报方式?怎样比较回报资金的大小?
(1)比较三种方案的每日回报
(2)比较三种方案在若干天内的累计回报
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多 回报10元;
方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。
课 堂 讨 论
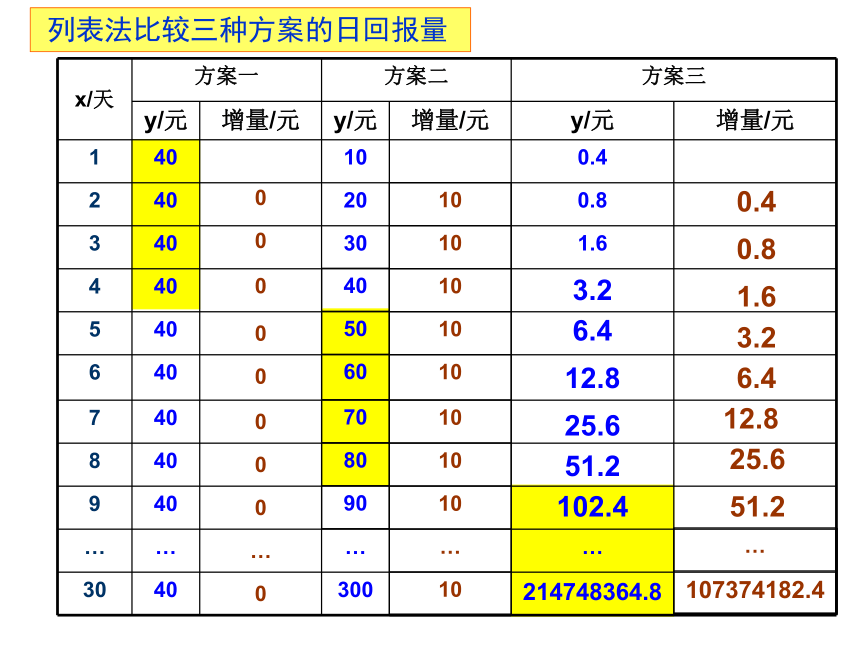
问题2:根据日回报中的数量关系,归纳概括相应的
函数模型?并写出每个方案的函数解析式?
问题3:如何在数据上比较日回报增长的快慢呢?
通过比较各个方案后一天与前一天的日回报差,
即日回报的增加量。
x/天
方案一
方案二
方案三
y/元
增量/元
y/元
增量/元
y/元
增量/元
1
40
10
0.4
2
40
20
0.8
3
40
30
1.6
4
40
5
40
6
40
7
40
8
40
9
40
…
…
…
…
30
40
300
40
50
60
70
80
90
102.4
51.2
25.6
12.8
6.4
3.2
列表法比较三种方案的日回报量
0
0
0
0
0
0
0
0
…
0
10
10
10
10
10
10
10
10
…
10
0.4
0.8
…
107374182.4
1.6
3.2
6.4
12.8
25.6
51.2
214748364.8
1
2
3
4
6
5
7
8
9
10
20
0
40
60
80
100
120
140
y
x
方案一:y=40
1
2
3
4
5
6
7
8
9
10
…
40
40
40
40
40
40
40
40
40
40
…
x
方案二
y=10x
1
2
3
4
5
6
7
8
9
10
…
10
20
30
40
50
60
70
80
90
100
…
x
y=0.4*2x-1
1
2
3
4
5
6
7
8
9
10
…
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
204.8
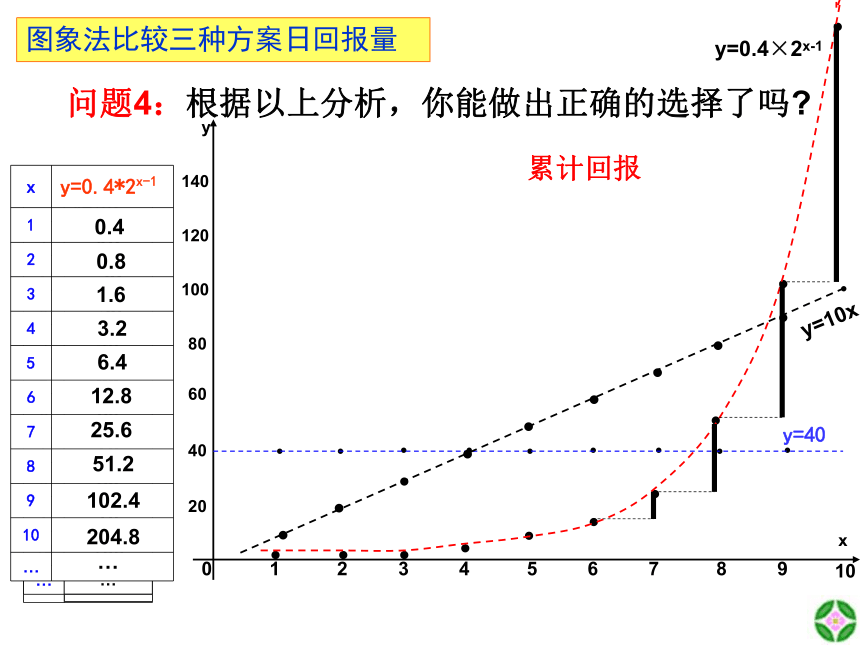
图象法比较三种方案日回报量
y=40
y=10x
y=0.4×2x-1
x
…
问题4:根据以上分析,你能做出正确的选择了吗?
累计回报
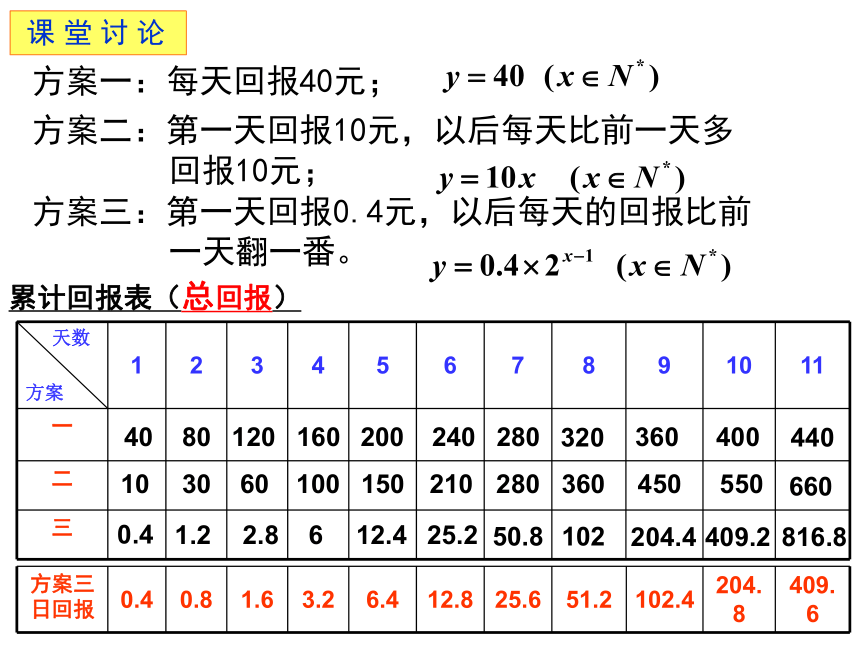
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多 回报10元;
方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。
课 堂 讨 论
累计回报表(总回报)
天数
方案
1
2
3
4
5
6
7
8
9
10
11
一
二
三
方案三日回报
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
204.8
409.6
40
80
120
160
200
240
280
320
360
400
440
10
30
60
100
150
210
280
360
450
550
660
0.4
1.2
2.8
6
12.4
25.2
50.8
102
204.4
409.2
816.8
累计回报表
天数
方案
1
2
3
4
5
6
7
8
9
10
11
一
二
三
40
80
120
160
200
240
280
320
360
400
440
10
30
60
100
150
210
280
360
450
550
660
0.4
1.2
2.8
6
12.4
25.2
50.8
102
204.4
409.2
816.8
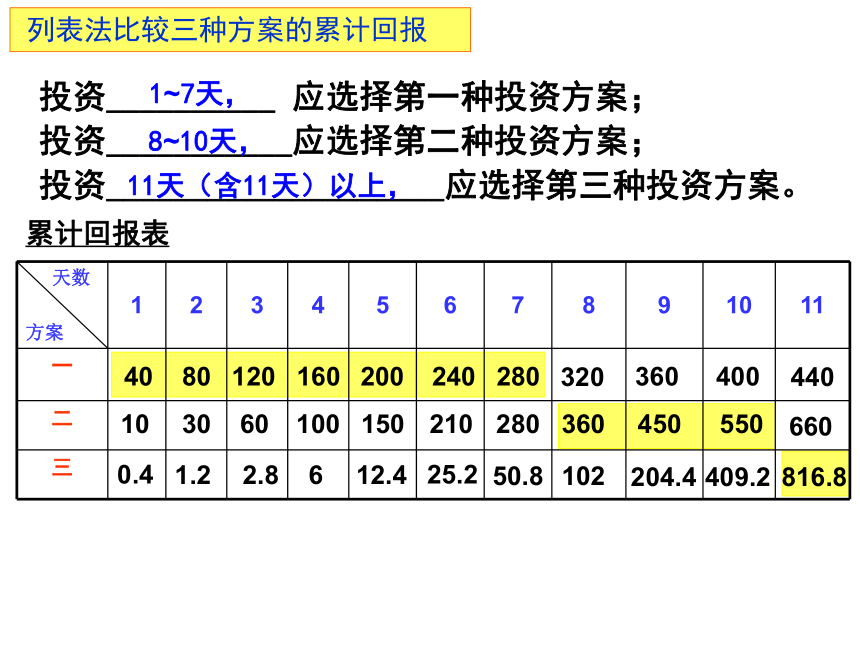
投资__________ 应选择第一种投资方案;
投资___________应选择第二种投资方案;
投资____________________应选择第三种投资方案。
11天(含11天)以上,
8~10天,
1~7天,
列表法比较三种方案的累计回报
生活场景小应用
如果你是老板,你会选择以哪种函数模型给员工发工资呢?一次函数?指数函数?说说你的依据?
虽然一次函数和指数函数都有增长,但是它们的增长态势各具特点。当自变量很大时,指数型函数比一次函数增长快得多,两者的增长速度不在一个档次上。
通过例1,你能否归纳解决实际问题的方法?
把实际问题抽象成一个函数模型,用解析式,数据表格,图象这三种函数的表示法研究实际问题。
例2 某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:
y=0.25X,y=log7x+1 , y=1.002x ,其中哪个模型能符合公司的要求?
例题讲解
问题1:公司的要求到底意味着怎样的数学关系?
(1)奖金总数不超过5万元
(2)奖金不超过利润的25%
问题2:你能结合各函数模型的图象初步判定这三个增长型函数哪个符合限制条件?
解: 借助计算机作出函数
的图象
400
600
800
1000
1200
200
1
2
3
4
5
6
7
8
x
y
o
y=5
y=0.25x
通过观察函数图象得到初步结论:
对比三种函数模型的增长差异
按对数模型进行奖励时符合公司的要求
三种奖金的函数模型
x
y=0.25x
y=log7x+1
y=1.002x
100
200
300
400
500
600
700
800
900
1000
0.1
0.08
0.07
0.06
0.05
125
150
175
200
225
250
4.19
4.29
2.72
3.32
4.05
4.95
6.04
7.37
25
25
25
25
25
25
25
25
25
0.27
0.33
0.4
0.5
0.6
0.73
0.9
1.09
1.33
增量△y
增量△y
增量△y
25
50
75
100
4.37
4.44
4.5
4.55
0.35
0.21
0.15
0.11
3.37
3.72
3.93
4.08
1.22
1.49
1.82
2.22
解: 借助计算机作出函数
的图象
400
600
800
1000
1200
200
1
2
3
4
5
6
7
8
x
y
o
y=5
y=0.25x
下面列表计算确认上述判断:
2.5
1.02
2.18
5
1.04
2.54
…
…
…
4.95
4.44
5.04
4.442
…
…
…
4.55
模型
奖金/万元
利润
10
20
800
810
1000
…
…
y=0.25X
问题:当 时,奖金是否不超过利润的25%呢?
等价于对任意的
我们来看函数 的图象:
7
综上所述:模型 确实符合公司要求.
1
log
+
=
x
y
生活场景小应用
人口老龄化危机是中国在本世纪面临的一大挑战。如果你是官员,那么你希望我国未来100年人口以哪种函数模型增长?一次函数?指数函数?对数函数?说说你的依据?
对数函数呈现先快后慢的态势,特别当自变量很大时,对数函数的增长趋近于平缓。
这节课你学习到了哪些知识?谈谈你的收获?
2. 几类增长函数建模的步骤
1. 几类不同函数模型的增长差异
随 堂 小结
1.书本107 1,2,3
2. 有人说把一张普通的纸(厚度约为0.075mm )对折32次,它的高度比喜马拉雅山还要高,你相信吗?为什么?
3.查阅《罗马俱乐部关于人类困境的报告》
[美]?丹尼斯·米都斯?等著。
第一章 指数增长的本质
第二章 指数增长的极限
…………
课 后 作 业
课 堂 引 入
思考:在生活中,你能举出增长的例子吗?
函数是描述客观世界变化规律的基本数学模型不同的增长规律需要不同的函数模型来描述的,我们学过的函数模型有哪些呢?
一次函数,二次函数,指数函数,对数函数,幂函数等等
对于实际问题,我们如何选择一个恰当的函数模型来刻画它呢?
找出模型后又是如何去研究它的增长规律呢?
例1.假如你有一笔资金用于投资,现有三种方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元以后每天比前一天多10元
方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。
请问,你会选择哪种投资方案?
提 出 问 题
问题1:你会选择什么样的回报方式?怎样比较回报资金的大小?
(1)比较三种方案的每日回报
(2)比较三种方案在若干天内的累计回报
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多 回报10元;
方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。
课 堂 讨 论
问题2:根据日回报中的数量关系,归纳概括相应的
函数模型?并写出每个方案的函数解析式?
问题3:如何在数据上比较日回报增长的快慢呢?
通过比较各个方案后一天与前一天的日回报差,
即日回报的增加量。
x/天
方案一
方案二
方案三
y/元
增量/元
y/元
增量/元
y/元
增量/元
1
40
10
0.4
2
40
20
0.8
3
40
30
1.6
4
40
5
40
6
40
7
40
8
40
9
40
…
…
…
…
30
40
300
40
50
60
70
80
90
102.4
51.2
25.6
12.8
6.4
3.2
列表法比较三种方案的日回报量
0
0
0
0
0
0
0
0
…
0
10
10
10
10
10
10
10
10
…
10
0.4
0.8
…
107374182.4
1.6
3.2
6.4
12.8
25.6
51.2
214748364.8
1
2
3
4
6
5
7
8
9
10
20
0
40
60
80
100
120
140
y
x
方案一:y=40
1
2
3
4
5
6
7
8
9
10
…
40
40
40
40
40
40
40
40
40
40
…
x
方案二
y=10x
1
2
3
4
5
6
7
8
9
10
…
10
20
30
40
50
60
70
80
90
100
…
x
y=0.4*2x-1
1
2
3
4
5
6
7
8
9
10
…
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
204.8
图象法比较三种方案日回报量
y=40
y=10x
y=0.4×2x-1
x
…
问题4:根据以上分析,你能做出正确的选择了吗?
累计回报
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多 回报10元;
方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。
课 堂 讨 论
累计回报表(总回报)
天数
方案
1
2
3
4
5
6
7
8
9
10
11
一
二
三
方案三日回报
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
204.8
409.6
40
80
120
160
200
240
280
320
360
400
440
10
30
60
100
150
210
280
360
450
550
660
0.4
1.2
2.8
6
12.4
25.2
50.8
102
204.4
409.2
816.8
累计回报表
天数
方案
1
2
3
4
5
6
7
8
9
10
11
一
二
三
40
80
120
160
200
240
280
320
360
400
440
10
30
60
100
150
210
280
360
450
550
660
0.4
1.2
2.8
6
12.4
25.2
50.8
102
204.4
409.2
816.8
投资__________ 应选择第一种投资方案;
投资___________应选择第二种投资方案;
投资____________________应选择第三种投资方案。
11天(含11天)以上,
8~10天,
1~7天,
列表法比较三种方案的累计回报
生活场景小应用
如果你是老板,你会选择以哪种函数模型给员工发工资呢?一次函数?指数函数?说说你的依据?
虽然一次函数和指数函数都有增长,但是它们的增长态势各具特点。当自变量很大时,指数型函数比一次函数增长快得多,两者的增长速度不在一个档次上。
通过例1,你能否归纳解决实际问题的方法?
把实际问题抽象成一个函数模型,用解析式,数据表格,图象这三种函数的表示法研究实际问题。
例2 某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:
y=0.25X,y=log7x+1 , y=1.002x ,其中哪个模型能符合公司的要求?
例题讲解
问题1:公司的要求到底意味着怎样的数学关系?
(1)奖金总数不超过5万元
(2)奖金不超过利润的25%
问题2:你能结合各函数模型的图象初步判定这三个增长型函数哪个符合限制条件?
解: 借助计算机作出函数
的图象
400
600
800
1000
1200
200
1
2
3
4
5
6
7
8
x
y
o
y=5
y=0.25x
通过观察函数图象得到初步结论:
对比三种函数模型的增长差异
按对数模型进行奖励时符合公司的要求
三种奖金的函数模型
x
y=0.25x
y=log7x+1
y=1.002x
100
200
300
400
500
600
700
800
900
1000
0.1
0.08
0.07
0.06
0.05
125
150
175
200
225
250
4.19
4.29
2.72
3.32
4.05
4.95
6.04
7.37
25
25
25
25
25
25
25
25
25
0.27
0.33
0.4
0.5
0.6
0.73
0.9
1.09
1.33
增量△y
增量△y
增量△y
25
50
75
100
4.37
4.44
4.5
4.55
0.35
0.21
0.15
0.11
3.37
3.72
3.93
4.08
1.22
1.49
1.82
2.22
解: 借助计算机作出函数
的图象
400
600
800
1000
1200
200
1
2
3
4
5
6
7
8
x
y
o
y=5
y=0.25x
下面列表计算确认上述判断:
2.5
1.02
2.18
5
1.04
2.54
…
…
…
4.95
4.44
5.04
4.442
…
…
…
4.55
模型
奖金/万元
利润
10
20
800
810
1000
…
…
y=0.25X
问题:当 时,奖金是否不超过利润的25%呢?
等价于对任意的
我们来看函数 的图象:
7
综上所述:模型 确实符合公司要求.
1
log
+
=
x
y
生活场景小应用
人口老龄化危机是中国在本世纪面临的一大挑战。如果你是官员,那么你希望我国未来100年人口以哪种函数模型增长?一次函数?指数函数?对数函数?说说你的依据?
对数函数呈现先快后慢的态势,特别当自变量很大时,对数函数的增长趋近于平缓。
这节课你学习到了哪些知识?谈谈你的收获?
2. 几类增长函数建模的步骤
1. 几类不同函数模型的增长差异
随 堂 小结
1.书本107 1,2,3
2. 有人说把一张普通的纸(厚度约为0.075mm )对折32次,它的高度比喜马拉雅山还要高,你相信吗?为什么?
3.查阅《罗马俱乐部关于人类困境的报告》
[美]?丹尼斯·米都斯?等著。
第一章 指数增长的本质
第二章 指数增长的极限
…………
课 后 作 业
