人教A版高中数学必修1第三章3.2.1 几类不同增长的函数模型课件(19张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第三章3.2.1 几类不同增长的函数模型课件(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 520.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 22:25:11 | ||
图片预览



文档简介
3.2.1 几类不同
增长的函数模型
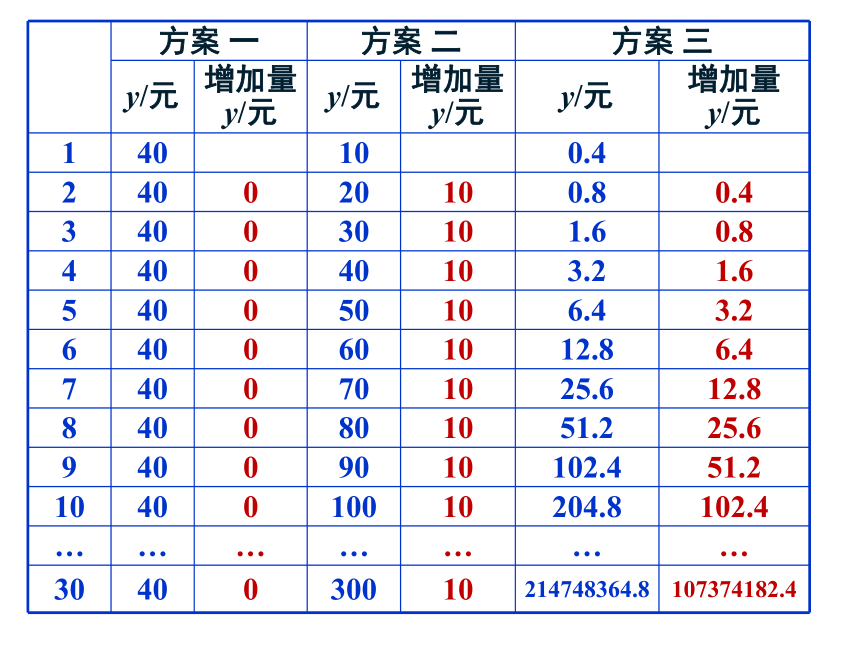
例1 假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
请问,你会选择哪种投资方案?
第一天回报10元,以后每天比前 一天多回报10元;
方案二:
第一天回报0.4元,以后每天的回报比前一天翻一番.
方案三:
方案 一
方案 二
方案 三
y/元
增加量
y/元
y/元
增加量
y/元
y/元
增加量
y/元
1
40
10
0.4
2
40
0
20
10
0.8
0.4
3
40
0
30
10
1.6
0.8
4
40
0
40
10
3.2
1.6
5
40
0
50
10
6.4
3.2
6
40
0
60
10
12.8
6.4
7
40
0
70
10
25.6
12.8
8
40
0
80
10
51.2
25.6
9
40
0
90
10
102.4
51.2
10
40
0
100
10
204.8
102.4
…
…
…
…
…
…
…
30
40
0
300
10
214748364.8
107374182.4
方案一 可以用函数 进行描述
方案二 可以用函数 进行描述
方案三 可以用函数
进行描述
20
40
60
80
100
120
2
4
6
8
10
O
y
x
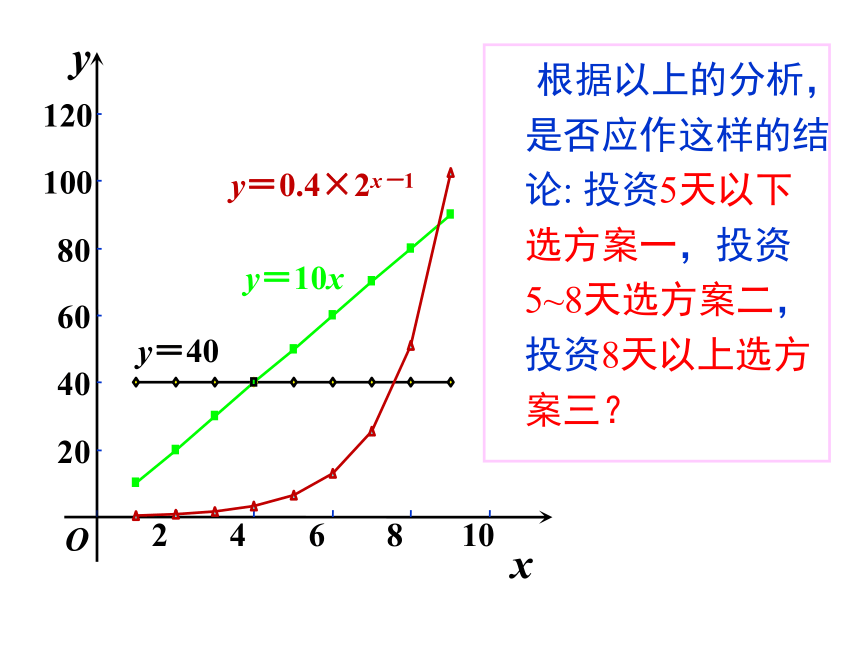
y=40
y=10x
根据以上的分析,是否应作这样的结论: 投资5天以下选方案一,投资5~8天选方案二,投资8天以上选方案三?
y=0.4×2x-1
819
409
204
102
50.8
25
12
6
2.8
1.2
0.4
三
660
550
450
360
280
210
150
100
60
30
10
二
440
400
360
320
280
240
200
160
120
80
40
一
11
10
9
8
7
6
5
4
3
2
1
天数
回报/元
方案
3276
1638
910
780
520
480
13
12
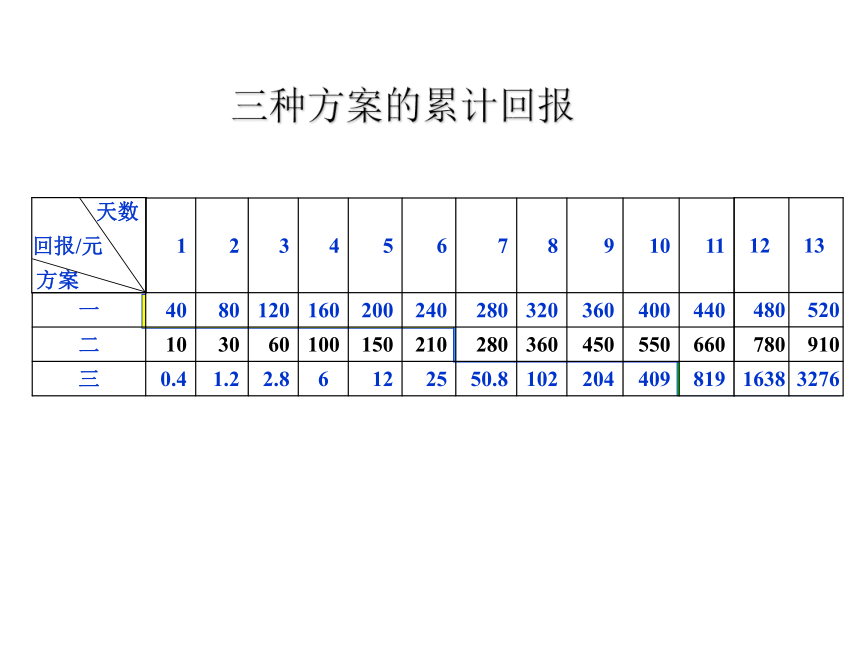
三种方案的累计回报
819
409
204
102
50.8
25
12
6
2.8
1.2
0.4
三
660
550
450
360
280
210
150
100
60
30
10
二
440
400
360
320
280
240
200
160
120
80
40
一
11
10
9
8
7
6
5
4
3
2
1
天数
回报/元
方案
3276
1638
910
780
520
480
13
12
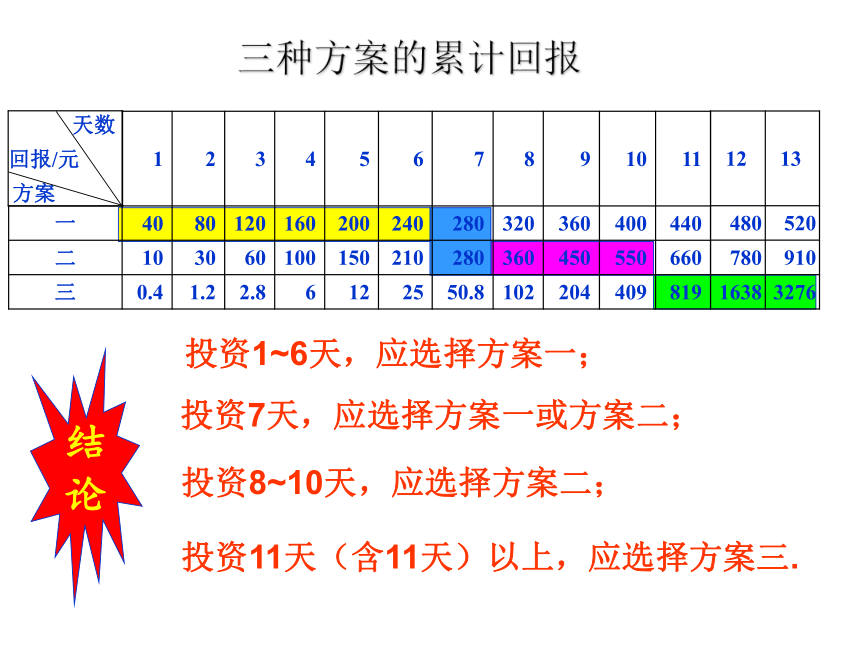
三种方案的累计回报
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三.
结
论
例2 某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的方案 :在销售利润达到10万元时,按销售利润进行奖励且奖金(单位: 万元)随销售利润 (单位: 万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%,现有三个奖励模型:
其中哪个模型能符合公司的要求?
解:借助计算器或计算机作出函数y=0.25x,
y=log7x+1,y=1.002x的图象(图3.2-2)
200
400
600
800
1000
1
2
3
5
4
6
8
7
O
x
y
y=0.25x
y=5
y=log7x+1
y=1.002x
观察图象发现,在区间[10,1000]上,模型y=0.25x,y=1.002x的图象都有一部分在直线y=5的上方,只有模型y=log7x+1的图象始终在y=5的下方,这说明只有按模型y=log7x+1进行奖励时才符合公司的要求.
下面通过计算确认上述判断.
首先计算哪个模型的奖金总数不超过5万.
对于模型y=0.25x,它在区间[10,1000]上递增,而且当x=20时,y=5,因此,当x>20时,y>5,所以该模型不符合要求;
对于模型y=1.002x,由函数图象,并利用计算器,可知在区间(805,806)内有一个点x0满足 ,由于它在区间[10,1000]上递增,因此当x>x0时,y>5,所以该模型也不符合要求;
对于模型y=log7x+1,它在区间[10,1000]上递增,而且当x=1000时,y=log71000+1≈4.55<5,所以它符合奖金总数不超过5万元的要求.
再计算按模型y=log7x+1奖励时,奖金是否不超过利润的25%,即当x∈[10,1000]时,是否有
成立.
令 f (x) =log7x+1-0.25x,x∈[10,1000].
利用计算器或计算机作出函数 f(x) 的图象(图3.2-3)
200
400
600
800
1000
1200
-250
-300
-200
-150
-100
-50
O
x
y
由图象可知它是递减的,因此
f(x) 即 log7x+1<0.25x.
所以当x∈[10,1000]时,
说明按模型y=log7x+1奖励,奖金不会超过利润的25%.
综上所述,模型y=log7x+1确实能符合公司要求.
小 结
1.不同增长的函数模型的增长特点:
一次函数
指数函数
对数函数
直线上升
匀速增长
急剧上升
爆炸式增长
平缓增长
(1)审题理解题意;
(2)挖掘数量关系,建立数学模型;
(3)求解数学问题;
(4)回归实际,解决应用问题。
2、求解数学应用问题的一般步骤:
1、四个变量 随变量 变化的数据如下表:
1.005
1.0151
1.0461
1.1407
1.4295
2.3107
5
155
130
105
80
55
30
5
33733
1758.2
94.478
5
4505
3130
2005
1130
505
130
5
30
25
20
15
10
5
0
关于x呈指数型函数变化的变量是
2、某种计算机病毒是通过电子邮件进行传播的,如果
某台计算机感染上这种病毒,那么它就会在下一轮病毒
发作时传播一次病毒,并感染其他20台未被感染病毒的
计算机。现有10台计算机被第1轮病毒感染,问被第5轮
病毒感染的计算机有多少台?
解:设第 轮感染病毒的计算机为 ,则由已知得后一轮感染病毒的计算机是前一轮的20倍,且 ,
课 后 作 业
2. 习题 3.2 A组 1、2
1. 阅读教材P.98~ P.101.
增长的函数模型
例1 假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
请问,你会选择哪种投资方案?
第一天回报10元,以后每天比前 一天多回报10元;
方案二:
第一天回报0.4元,以后每天的回报比前一天翻一番.
方案三:
方案 一
方案 二
方案 三
y/元
增加量
y/元
y/元
增加量
y/元
y/元
增加量
y/元
1
40
10
0.4
2
40
0
20
10
0.8
0.4
3
40
0
30
10
1.6
0.8
4
40
0
40
10
3.2
1.6
5
40
0
50
10
6.4
3.2
6
40
0
60
10
12.8
6.4
7
40
0
70
10
25.6
12.8
8
40
0
80
10
51.2
25.6
9
40
0
90
10
102.4
51.2
10
40
0
100
10
204.8
102.4
…
…
…
…
…
…
…
30
40
0
300
10
214748364.8
107374182.4
方案一 可以用函数 进行描述
方案二 可以用函数 进行描述
方案三 可以用函数
进行描述
20
40
60
80
100
120
2
4
6
8
10
O
y
x
y=40
y=10x
根据以上的分析,是否应作这样的结论: 投资5天以下选方案一,投资5~8天选方案二,投资8天以上选方案三?
y=0.4×2x-1
819
409
204
102
50.8
25
12
6
2.8
1.2
0.4
三
660
550
450
360
280
210
150
100
60
30
10
二
440
400
360
320
280
240
200
160
120
80
40
一
11
10
9
8
7
6
5
4
3
2
1
天数
回报/元
方案
3276
1638
910
780
520
480
13
12
三种方案的累计回报
819
409
204
102
50.8
25
12
6
2.8
1.2
0.4
三
660
550
450
360
280
210
150
100
60
30
10
二
440
400
360
320
280
240
200
160
120
80
40
一
11
10
9
8
7
6
5
4
3
2
1
天数
回报/元
方案
3276
1638
910
780
520
480
13
12
三种方案的累计回报
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三.
结
论
例2 某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的方案 :在销售利润达到10万元时,按销售利润进行奖励且奖金(单位: 万元)随销售利润 (单位: 万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%,现有三个奖励模型:
其中哪个模型能符合公司的要求?
解:借助计算器或计算机作出函数y=0.25x,
y=log7x+1,y=1.002x的图象(图3.2-2)
200
400
600
800
1000
1
2
3
5
4
6
8
7
O
x
y
y=0.25x
y=5
y=log7x+1
y=1.002x
观察图象发现,在区间[10,1000]上,模型y=0.25x,y=1.002x的图象都有一部分在直线y=5的上方,只有模型y=log7x+1的图象始终在y=5的下方,这说明只有按模型y=log7x+1进行奖励时才符合公司的要求.
下面通过计算确认上述判断.
首先计算哪个模型的奖金总数不超过5万.
对于模型y=0.25x,它在区间[10,1000]上递增,而且当x=20时,y=5,因此,当x>20时,y>5,所以该模型不符合要求;
对于模型y=1.002x,由函数图象,并利用计算器,可知在区间(805,806)内有一个点x0满足 ,由于它在区间[10,1000]上递增,因此当x>x0时,y>5,所以该模型也不符合要求;
对于模型y=log7x+1,它在区间[10,1000]上递增,而且当x=1000时,y=log71000+1≈4.55<5,所以它符合奖金总数不超过5万元的要求.
再计算按模型y=log7x+1奖励时,奖金是否不超过利润的25%,即当x∈[10,1000]时,是否有
成立.
令 f (x) =log7x+1-0.25x,x∈[10,1000].
利用计算器或计算机作出函数 f(x) 的图象(图3.2-3)
200
400
600
800
1000
1200
-250
-300
-200
-150
-100
-50
O
x
y
由图象可知它是递减的,因此
f(x)
所以当x∈[10,1000]时,
说明按模型y=log7x+1奖励,奖金不会超过利润的25%.
综上所述,模型y=log7x+1确实能符合公司要求.
小 结
1.不同增长的函数模型的增长特点:
一次函数
指数函数
对数函数
直线上升
匀速增长
急剧上升
爆炸式增长
平缓增长
(1)审题理解题意;
(2)挖掘数量关系,建立数学模型;
(3)求解数学问题;
(4)回归实际,解决应用问题。
2、求解数学应用问题的一般步骤:
1、四个变量 随变量 变化的数据如下表:
1.005
1.0151
1.0461
1.1407
1.4295
2.3107
5
155
130
105
80
55
30
5
33733
1758.2
94.478
5
4505
3130
2005
1130
505
130
5
30
25
20
15
10
5
0
关于x呈指数型函数变化的变量是
2、某种计算机病毒是通过电子邮件进行传播的,如果
某台计算机感染上这种病毒,那么它就会在下一轮病毒
发作时传播一次病毒,并感染其他20台未被感染病毒的
计算机。现有10台计算机被第1轮病毒感染,问被第5轮
病毒感染的计算机有多少台?
解:设第 轮感染病毒的计算机为 ,则由已知得后一轮感染病毒的计算机是前一轮的20倍,且 ,
课 后 作 业
2. 习题 3.2 A组 1、2
1. 阅读教材P.98~ P.101.
