人教A版高中数学必修1第一章函数的奇偶性课件 (共19张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第一章函数的奇偶性课件 (共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览




文档简介
函数的奇偶性
生活中我们可以看到以下这些精美的图案
这些图形在初中我们称之为 图形,这种图形有什么特点?
沿着某一条直线折叠,直线两侧的图形能够完全重合
轴对称
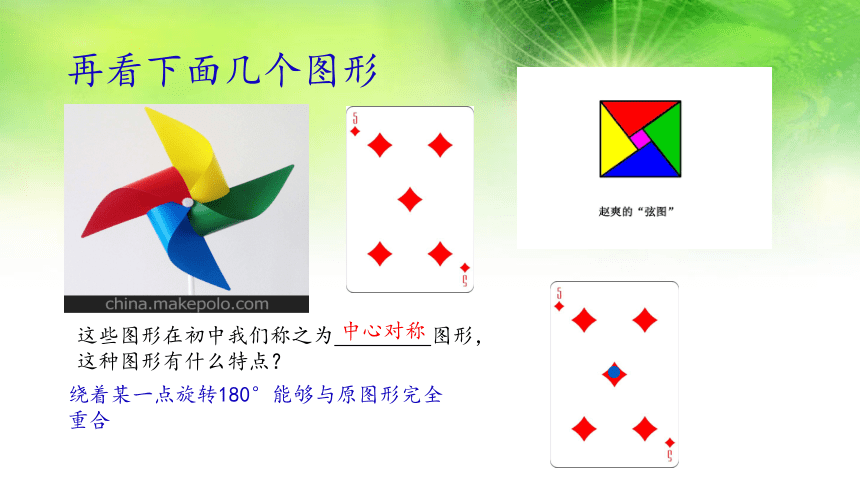
再看下面几个图形
这些图形在初中我们称之为 图形,这种图形有什么特点?
绕着某一点旋转180°能够与原图形完全重合
中心对称
●
对称美:
对称是指图形或物体相对某个点、直线或平面而言,在大小、形状和排列上具有一一对应的关系。相对我们而言对称美在生活中早已不是新鲜事物了,它是无处不在,无处不有的。对称的物体我们在数学课上也有一定程度上的接触。古希腊哲学家曾说过:“美的线条和其他一切美的形体都必须有对称的形式。”可能在我们睁开第一眼的时候,我们就已经发现对称美了。我们在婴儿时代所钟爱的五颜六色的玩具,无不显示对称美的张力。我们的孩童时代,开始学会感知的同时,我们相信,我们第一次欣赏的真正意义上的美,就是潜意识里认识的简单的对称美。对称美赋予了世界更加美丽的事物,我们生活在对称美的世界里,尽情享受着美的熏陶。而人类对对称美也有很深刻的认识和研究。
数学里也有对称美吗?
观察:
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
9
4
1
0
1
4
9
…
x
…
-3
-2
-1
0
1
2
3
…
f(x)=2-|x︱
…
-1
0
1
2
1
0
-1
…
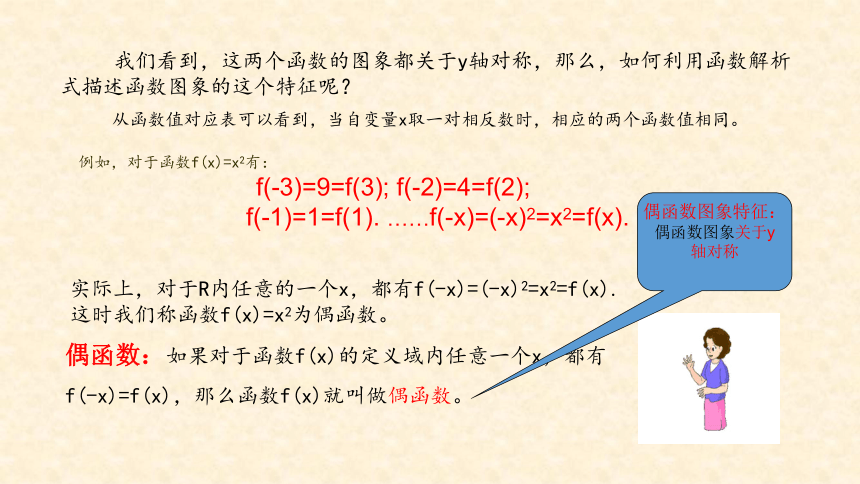
我们看到,这两个函数的图象都关于y轴对称,那么,如何利用函数解析式描述函数图象的这个特征呢?
从函数值对应表可以看到,当自变量x取一对相反数时,相应的两个函数值相同。
例如,对于函数f(x)=x2有:
f(-3)=9=f(3); f(-2)=4=f(2);
f(-1)=1=f(1). ……f(-x)=(-x)2=x2=f(x).
实际上,对于R内任意的一个x,都有f(-x)=(-x)2=x2=f(x).这时我们称函数f(x)=x2为偶函数。
偶函数:如果对于函数f(x)的定义域内任意一个x,都有
f(-x)=f(x),那么函数f(x)就叫做偶函数。
偶函数图象特征:偶函数图象关于y轴对称
观察:
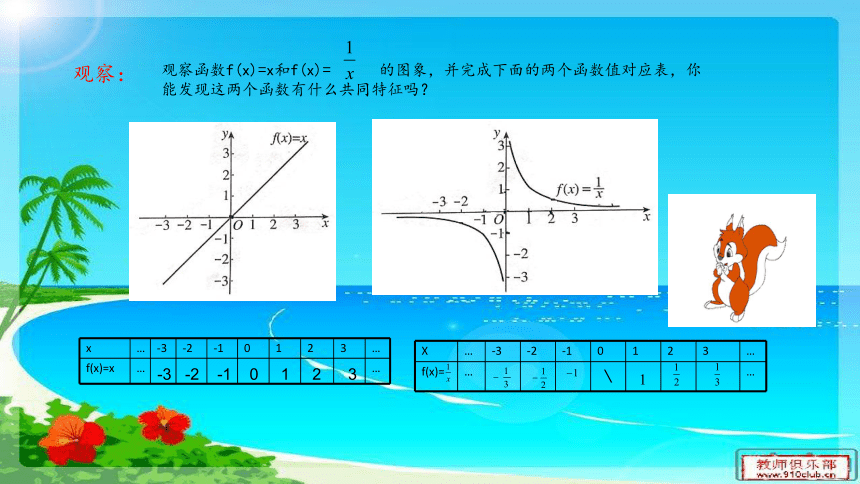
观察函数f(x)=x和f(x)= 的图象,并完成下面的两个函数值对应表,你能发现这两个函数有什么共同特征吗?
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x
…
…
X
…
-3
-2
-1
0
1
2
3
…
f(x)=
…
﹨
…
-3 -2 -1 0 1 2 3
我们看到,两个函数的图象都关于原点对称,函数图象的这个特征,反映在函数解析式上就是:
当自变量x取一对相反数时,相应的函数值f(x)也是一对相反数。
例如,对于函数f(x)=x有:
f(-3)=-3=-f(3);f(-2)=-2=-f(2);
f(-1)=-1=-f(1).
…… f(-x)=-x=-f(x)
实际上,对于函数f(x)=x定义域R内任意一个x, 都有f(-x)=-f(x),这时我们称函数f(x)=x为奇函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有
f(-x)=-f(x),那么函数f(x)就叫做奇函数
奇函数的图象特征:奇函数的图象关于原点对称
判断函数奇偶性注意事项:
(1)函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
(2)由函数的奇偶性定义,可知函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称);
(3)具有奇偶性的函数的图象的特征:偶函数的图象关于y轴对称,奇函数的图象关于原点对称;
(4)可以利用图象判断函数的奇偶性,这种方法称为图象法,也可以利用奇偶函数的定义判断函数的奇偶性,这种方法称为定义法;
(5)函数的奇偶性是函数在定义域上的性质是“整体”性质,而函数的单调性是函数在定义域的子集上的性质是“局部”性质.
因此,判断函数f(x)的奇偶性的步骤:
(1)先判断定义域是否关于原点对称
(2)再求f(-x),
若f(-x)=f(x),则为偶函数;
若f(-x)=-f(x),则为奇函数
典型例题分析演练
解析:
(1)∵f(x)的定义域为﹛x|x≠-1﹜,不关于原点对称
∴f(x)既不是奇函数,也不是偶函数
(2) ∵f(x)的定义域为R,关于原点对称
f(-x)=(-x)3-2(-x)=-x3+2x=-(x3-2x)=-f(x)
∴f(x) 是奇函数
(3)∵f(x)的定义域为R,关于原点对称
f(-x)=
=f(x)
∴f(x) 是偶函数
解析:(1)非奇非偶函数
(2)偶函数
(3)既是奇函数又是偶函数
点评:在奇函数与偶函数的定义中,都要求x∈D,-x∈D,这就是说,一个函数不论是奇函数还是偶函数,它的定义域都一定关于坐标原点对称.如果一个函数的定义域关于坐标原点不对称,那么这个函数就失去了是奇函数或是偶函数的前提条件,即这个函数既不是奇函数也不是偶函数.
函数的定义域是使函数有意义的自变量的取值范围,对定义域内任意x,其相反数-x也在函数的定义域内,此时称为定义域关于原点对称.
解析:f(x)为偶函数,偶函数图象关于y轴对称
解析:由于奇函数图象关于原点对称,在图象上我们可以画出f(x)在区间[-5,0)的图象,如图所示
结合图象可知:f(x)>0的x的取值集合为
{x|-5点评:注意数形结合思想的运用
解析:方法(1)利用定义确定a的值
方法(2)利用特殊值,f(-4)=f(4)可得a=4
解析:由定义域关于原点对称可得a-1=2a,a=-1,再由二次函数是偶函数,图象关于y轴对称,对称轴为0,b=0
4
-1
0
点评:利用函数奇偶性求参数值的常见类型及求解策略:
(1)定义域含参数:奇(偶)函数的定义域为[a,b],根据定义域关于原点对称,可以利用a+b=0求参数
(2)解析式含参数:根据f(-x)=-f(x)或f(-x)=f(x)列示,比较系数可解。或者利用特值法也可解,当然,所取特值应在定义域内取。
解析:当x>0时,则-x<0,代入x<0时的解析式得:f(-x)=-x(1+x),因为f(x)是R上的奇函数,有f(-x)=-f(x),所以f(x) =x(1+x)。而f(0)=0
所以f(x)的解析式为:
解析:当x∈(-∞,0)时,则-x ∈(0,+∞),
f(-x)=(-x)2+(-x)-1=x2-x-1,
因为f(x)为偶函数,f(-x)=f(x)
所以,当x∈(-∞,0)时, f(x) =x2-x-1
点评:(1)若f(x)是奇函数,f(0)=0;
(2)已知函数的奇偶性和函数在某区间上的解析式,求该函数在与已知区间关于原点对称的区间上的解析式时,首先设出所求区间上的自变量利用奇、偶函数的定义域关于原点对称的特点,把它转化到已知解析式的区间上,代入已知的解析式,然后再次利用函数的奇偶性求解即可。
小结与反思:
本节课学习了函数的奇偶性的定义
偶函数:如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数
判断函数f(x)的奇偶性的步骤:
(1)先判断定义域是否关于原点对称
(2)再求f(-x),若f(-x)=f(x),则为偶函数;
若f(-x)=-f(x),则为奇函数
作业:P36 ,1,2,练习册
谢谢指导
生活中我们可以看到以下这些精美的图案
这些图形在初中我们称之为 图形,这种图形有什么特点?
沿着某一条直线折叠,直线两侧的图形能够完全重合
轴对称
再看下面几个图形
这些图形在初中我们称之为 图形,这种图形有什么特点?
绕着某一点旋转180°能够与原图形完全重合
中心对称
●
对称美:
对称是指图形或物体相对某个点、直线或平面而言,在大小、形状和排列上具有一一对应的关系。相对我们而言对称美在生活中早已不是新鲜事物了,它是无处不在,无处不有的。对称的物体我们在数学课上也有一定程度上的接触。古希腊哲学家曾说过:“美的线条和其他一切美的形体都必须有对称的形式。”可能在我们睁开第一眼的时候,我们就已经发现对称美了。我们在婴儿时代所钟爱的五颜六色的玩具,无不显示对称美的张力。我们的孩童时代,开始学会感知的同时,我们相信,我们第一次欣赏的真正意义上的美,就是潜意识里认识的简单的对称美。对称美赋予了世界更加美丽的事物,我们生活在对称美的世界里,尽情享受着美的熏陶。而人类对对称美也有很深刻的认识和研究。
数学里也有对称美吗?
观察:
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
9
4
1
0
1
4
9
…
x
…
-3
-2
-1
0
1
2
3
…
f(x)=2-|x︱
…
-1
0
1
2
1
0
-1
…
我们看到,这两个函数的图象都关于y轴对称,那么,如何利用函数解析式描述函数图象的这个特征呢?
从函数值对应表可以看到,当自变量x取一对相反数时,相应的两个函数值相同。
例如,对于函数f(x)=x2有:
f(-3)=9=f(3); f(-2)=4=f(2);
f(-1)=1=f(1). ……f(-x)=(-x)2=x2=f(x).
实际上,对于R内任意的一个x,都有f(-x)=(-x)2=x2=f(x).这时我们称函数f(x)=x2为偶函数。
偶函数:如果对于函数f(x)的定义域内任意一个x,都有
f(-x)=f(x),那么函数f(x)就叫做偶函数。
偶函数图象特征:偶函数图象关于y轴对称
观察:
观察函数f(x)=x和f(x)= 的图象,并完成下面的两个函数值对应表,你能发现这两个函数有什么共同特征吗?
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x
…
…
X
…
-3
-2
-1
0
1
2
3
…
f(x)=
…
﹨
…
-3 -2 -1 0 1 2 3
我们看到,两个函数的图象都关于原点对称,函数图象的这个特征,反映在函数解析式上就是:
当自变量x取一对相反数时,相应的函数值f(x)也是一对相反数。
例如,对于函数f(x)=x有:
f(-3)=-3=-f(3);f(-2)=-2=-f(2);
f(-1)=-1=-f(1).
…… f(-x)=-x=-f(x)
实际上,对于函数f(x)=x定义域R内任意一个x, 都有f(-x)=-f(x),这时我们称函数f(x)=x为奇函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有
f(-x)=-f(x),那么函数f(x)就叫做奇函数
奇函数的图象特征:奇函数的图象关于原点对称
判断函数奇偶性注意事项:
(1)函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
(2)由函数的奇偶性定义,可知函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称);
(3)具有奇偶性的函数的图象的特征:偶函数的图象关于y轴对称,奇函数的图象关于原点对称;
(4)可以利用图象判断函数的奇偶性,这种方法称为图象法,也可以利用奇偶函数的定义判断函数的奇偶性,这种方法称为定义法;
(5)函数的奇偶性是函数在定义域上的性质是“整体”性质,而函数的单调性是函数在定义域的子集上的性质是“局部”性质.
因此,判断函数f(x)的奇偶性的步骤:
(1)先判断定义域是否关于原点对称
(2)再求f(-x),
若f(-x)=f(x),则为偶函数;
若f(-x)=-f(x),则为奇函数
典型例题分析演练
解析:
(1)∵f(x)的定义域为﹛x|x≠-1﹜,不关于原点对称
∴f(x)既不是奇函数,也不是偶函数
(2) ∵f(x)的定义域为R,关于原点对称
f(-x)=(-x)3-2(-x)=-x3+2x=-(x3-2x)=-f(x)
∴f(x) 是奇函数
(3)∵f(x)的定义域为R,关于原点对称
f(-x)=
=f(x)
∴f(x) 是偶函数
解析:(1)非奇非偶函数
(2)偶函数
(3)既是奇函数又是偶函数
点评:在奇函数与偶函数的定义中,都要求x∈D,-x∈D,这就是说,一个函数不论是奇函数还是偶函数,它的定义域都一定关于坐标原点对称.如果一个函数的定义域关于坐标原点不对称,那么这个函数就失去了是奇函数或是偶函数的前提条件,即这个函数既不是奇函数也不是偶函数.
函数的定义域是使函数有意义的自变量的取值范围,对定义域内任意x,其相反数-x也在函数的定义域内,此时称为定义域关于原点对称.
解析:f(x)为偶函数,偶函数图象关于y轴对称
解析:由于奇函数图象关于原点对称,在图象上我们可以画出f(x)在区间[-5,0)的图象,如图所示
结合图象可知:f(x)>0的x的取值集合为
{x|-5
解析:方法(1)利用定义确定a的值
方法(2)利用特殊值,f(-4)=f(4)可得a=4
解析:由定义域关于原点对称可得a-1=2a,a=-1,再由二次函数是偶函数,图象关于y轴对称,对称轴为0,b=0
4
-1
0
点评:利用函数奇偶性求参数值的常见类型及求解策略:
(1)定义域含参数:奇(偶)函数的定义域为[a,b],根据定义域关于原点对称,可以利用a+b=0求参数
(2)解析式含参数:根据f(-x)=-f(x)或f(-x)=f(x)列示,比较系数可解。或者利用特值法也可解,当然,所取特值应在定义域内取。
解析:当x>0时,则-x<0,代入x<0时的解析式得:f(-x)=-x(1+x),因为f(x)是R上的奇函数,有f(-x)=-f(x),所以f(x) =x(1+x)。而f(0)=0
所以f(x)的解析式为:
解析:当x∈(-∞,0)时,则-x ∈(0,+∞),
f(-x)=(-x)2+(-x)-1=x2-x-1,
因为f(x)为偶函数,f(-x)=f(x)
所以,当x∈(-∞,0)时, f(x) =x2-x-1
点评:(1)若f(x)是奇函数,f(0)=0;
(2)已知函数的奇偶性和函数在某区间上的解析式,求该函数在与已知区间关于原点对称的区间上的解析式时,首先设出所求区间上的自变量利用奇、偶函数的定义域关于原点对称的特点,把它转化到已知解析式的区间上,代入已知的解析式,然后再次利用函数的奇偶性求解即可。
小结与反思:
本节课学习了函数的奇偶性的定义
偶函数:如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数
判断函数f(x)的奇偶性的步骤:
(1)先判断定义域是否关于原点对称
(2)再求f(-x),若f(-x)=f(x),则为偶函数;
若f(-x)=-f(x),则为奇函数
作业:P36 ,1,2,练习册
谢谢指导
