高中数学人教A版必修1第一章1.3.1函数的单调性 课件(24张PPT)
文档属性
| 名称 | 高中数学人教A版必修1第一章1.3.1函数的单调性 课件(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 692.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览




文档简介
1.3.1 函数的单调性
第一课时
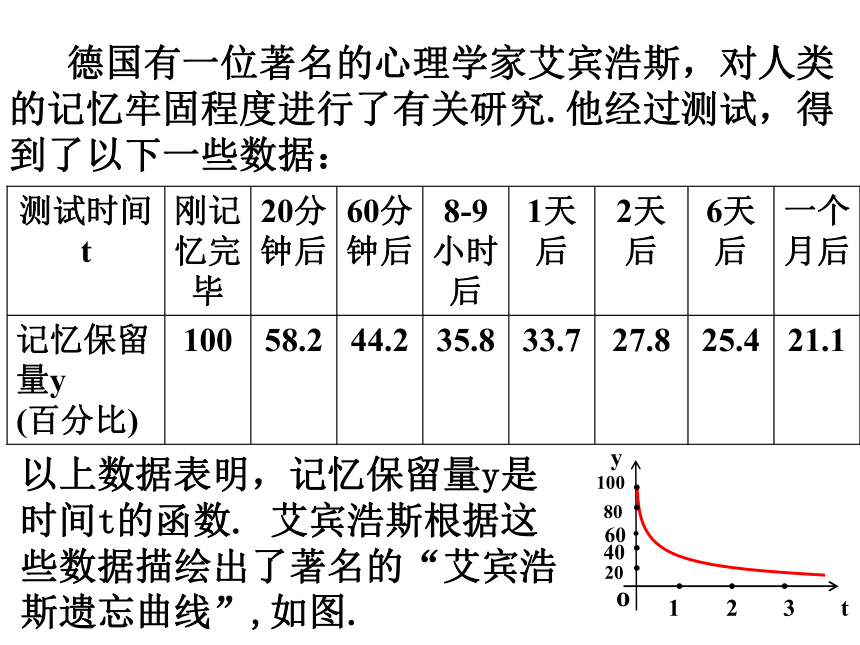
德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了以下一些数据:
测试时间 t
刚记忆完毕
20分钟后
60分钟后
8-9
小时后
1天后
2天后
6天后
一个月后
记忆保留量y
(百分比)
100
58.2
44.2
35.8
33.7
27.8
25.4
21.1
以上数据表明,记忆保留量y是
时间t的函数. 艾宾浩斯根据这
些数据描绘出了著名的“艾宾浩
斯遗忘曲线”,如图.
1
2
3
t
y
o
20
40
60
80
100
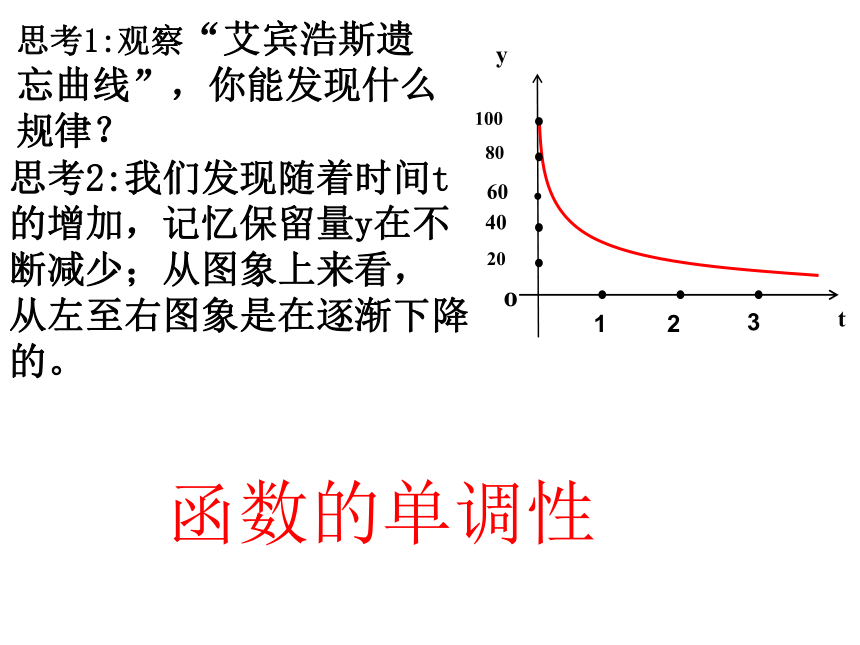
思考1:观察“艾宾浩斯遗忘曲线”,你能发现什么规律?
t
y
o
20
40
60
80
100
1
2
3
函数的单调性
思考2:我们发现随着时间t
的增加,记忆保留量y在不
断减少;从图象上来看,
从左至右图象是在逐渐下降
的。
x
y
o
-1
x
O
y
1
1
2
4
-1
-2
1
1.从左至右图象————
2.在区间 (-∞, +∞)上,随着x的增大,f(x)的值随着 ————
2.(0,+∞)上从左至右图象上升,
当x增大时f(x)随着增大
1
上升
增大
下降
1.(-∞,0]上从左至右图象
当x增大时f(x)随着
减小
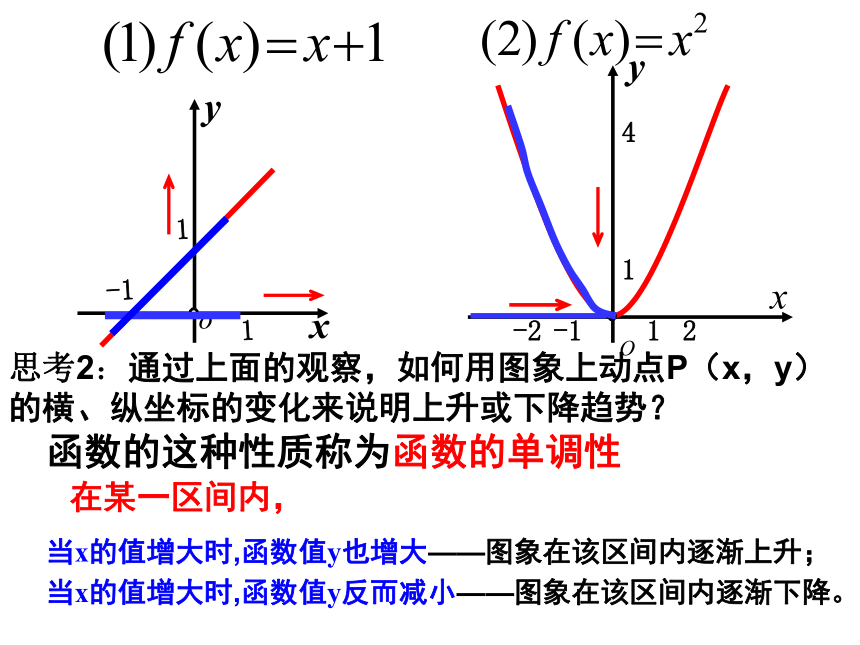
思考1:画出下列函数的图象,根据图象思考当
自变量x的值增大时,相应函数值是如何变化的?
x
y
o
-1
x
O
y
1
1
2
4
-1
-2
1
1
在某一区间内,
当x的值增大时,函数值y也增大——图象在该区间内逐渐上升;
当x的值增大时,函数值y反而减小——图象在该区间内逐渐下降。
函数的这种性质称为函数的单调性
思考2:通过上面的观察,如何用图象上动点P(x,y)的横、纵坐标的变化来说明上升或下降趋势?
思考3:如何用数学符号语言定义函数所具有的这种性质?
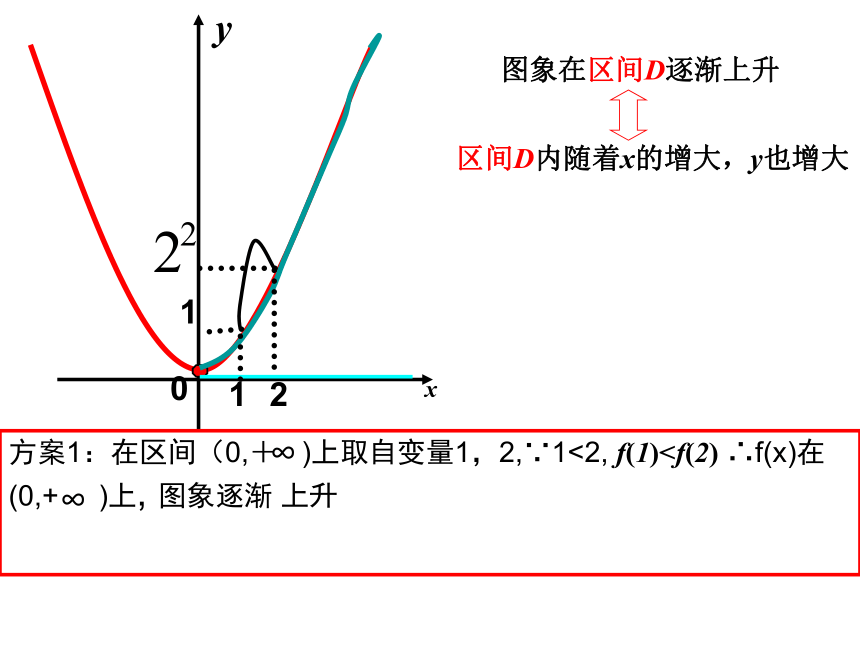
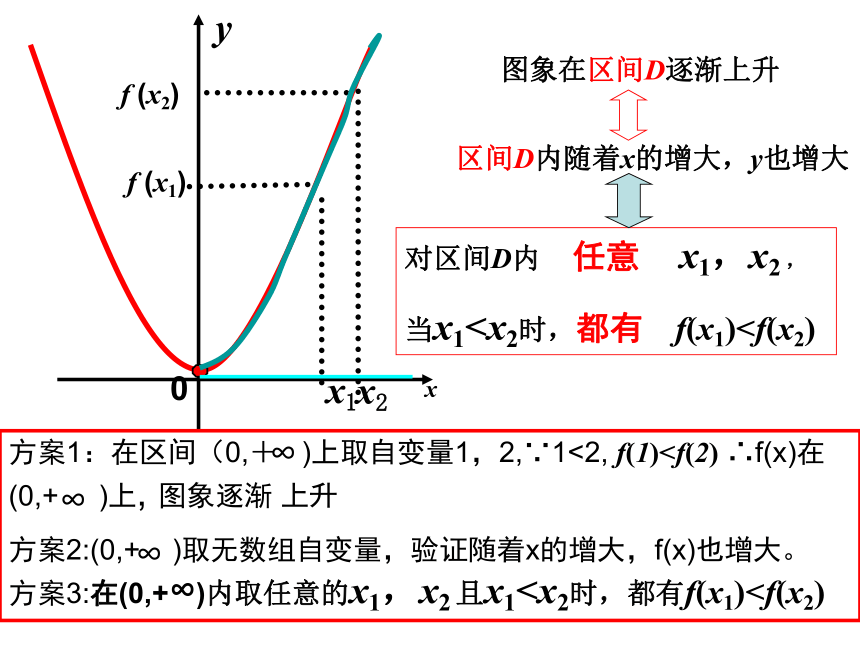
图象在区间D逐渐上升
区间D内随着x的增大,y也增大
x
0
1
2
1
y
方案1:在区间(0,+ )上取自变量1,2,∵1<2, f(1)∞
∞
方案二:
对区间D内 任意 x1,x2 ,
当x1图象在区间D逐渐上升
区间D内随着x的增大,y也增大
x
0
x1
x2
f (x1)
f (x2)
方案1:在区间(0,+ )上取自变量1,2,∵1<2, f(1)方案2:(0,+ )取无数组自变量,验证随着x的增大,f(x)也增大。
方案3:在(0,+∞)内取任意的x1,x2 且x1∞
∞
∞
y
对区间D内 x1,x2 ,
当x1都
设函数y=f(x)的定义域为I,区间D I.
定义
任意
如果对于区间D上的任意
两个自变量的值x1,x2,
当x1<
D称为 f (x)的单调
增区间.
那么就说 f (x)在区间D上
是单调增函数,
区间D内随着x的增大,y也增大
图象在区间D逐渐上升
0
x1
f (x1)
f (x2)
1
2
1
y
那么就说在f(x)这个区间上是单调
减函数,D称为f(x)的单调 减 区间.
O
x
y
x1
x2
f(x1)
f(x2)
类比单调增函数的研究方法定义单调减函数.
x
O
y
x1
x2
f(x1)
f(x2)
设函数y=f(x)的定义域为I,区间D I.
如果对于属于定义域I内某个区间D上
的任意两个自变量的值x1,x2,
设函数y=f(x)的定义域为I,区间D I.
如果对于属于定义域I内某个区间D上
的任意两个自变量的值x1,x2,
那么就说在f(x)这个区间上是单调增 函数,D称为f(x)的单调 区间.
增
当x1<
当x1>
单调区间
如果函数 y =f(x)在区间D是单调增函数或单调减函数,那么就说函数 y =f(x)在区间D上具有单调性。
(1)函数单调性是针对某个区间而言的,是一个局部性质;
判断1:函数 f (x)= x2 在 是单调增函数;
x
y
o
(2) x 1, x 2 取值的任意性
判断2:定义在R上的函数
f (x)满足 f (2)> f(1),则
函数 f (x)在R上是增函数;
y
x
O
1
2
f(1)
f(2)
解:函数y=f(x)的单调区间有[-5,-2),[-2,1) ,[1,3), [3,5].
例1. 如图是定义在闭区间[-5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调区间, 以及在每一单调区间上, 函数是增函数还是减函数?
其中y=f(x)在区间[-2,1),[3,5]上是增函数;
说明:1.区间端点处若有定义写开写闭均可.
2.图象法判断函数的单调性:从左向右看图象的升降情况
在区间[-5,-2),[1,3)上是减函数.
-4
3
2
1
5
4
3
1
2
-1
-2
-1
-5
-3
-2
x
y
O
练一练
根据下图说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数.
2
5
4
4
x
y
O
-1
3
2
1
解:函数y=f(x)的单调区间有[-1,0),[0,2) ,[2,4), [4,5].
其中y=f(x)在区间[0,2),[4,5]上是增函数;
在区间[-1,0),[2,4)上是减函数.
例2 证明函数 f(x) = 3 x+2在区间R上是增函数.
例2 证明函数 f(x) = 3 x+2在区间R上是增函数.
设 x1,x2 是 R上任意两个实数,且x1﹤x2
证明:
则 f(x1) - f(x2) = (3x1+2) - (3x2+2)
= 3(x1-x2)
由 x1﹤x2 ,得 x1 - x2﹤0
于是 f(x1) - f(x2) ﹤0
即 f(x1) ﹤ f(x2)
所以 f(x)=3x+2在R上是增函数
作差
设值
变形
定号
下结论
用定义证明函数单调性的四步骤:
(1)设值:
在所给区间上任意设两个实 数
(2)作差
(3)变形
作差
:常通过“因式分解”、“通分”、“配方”等
手段将差式变形为因式乘积或平方和形式
判断 的符号
(4)结论:
并作出单调性的结论
设量
判断差符号
作差变形
下结论
课堂小结
1. 两个定义:增函数、减函数的定义;
②(定义法)证明函数单调性,步骤:
①图象法判断函数的单调性:
增函数的图象从左到右
减函数的图象从左到右
上升
下降
3.一个数学思想:数形结合
2:两种方法
例2、物理学中的玻意耳定律 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大。试用函数的单调性证明之。
证明:
1
2
3
4
1.设值;
2.作差变形;
3.定号;
4.下结论
?
画出函数 图象,写出定义域并写出单调区间:
x
y
_____________
,
讨论:根据函数单调性的定义
拓展探究
y
O
x
在 (0,+∞) 上任取 x1、 x2
当x1< x2时,都有f(x1) f(x2)
>
y
O
x
-1
1
-1
1
取自变量-1< 1,
而 f(-1) f(1)
∴不能说 在(-∞,0)∪(0,+∞)上是减函数
要写成(-∞,0),(0,+∞)的形式。
<
逗号隔开
巩固
对区间D内 任意 x1,x2 ,
当x1图象在区间D逐渐上升
区间D内随着x的增大,y也增大
x
0
x1
x2
f (x1)
f (x2)
1
2
1
方案1:在区间(0,+ )上取自变量1,2,∵1<2, f(1)方案2:(0,+ )取无数组自变量,验证随着x的增大,f(x)也增大。
方案3:在(0,+∞)内取任意的x1,x2 且x1∞
∞
∞
y
第一课时
德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了以下一些数据:
测试时间 t
刚记忆完毕
20分钟后
60分钟后
8-9
小时后
1天后
2天后
6天后
一个月后
记忆保留量y
(百分比)
100
58.2
44.2
35.8
33.7
27.8
25.4
21.1
以上数据表明,记忆保留量y是
时间t的函数. 艾宾浩斯根据这
些数据描绘出了著名的“艾宾浩
斯遗忘曲线”,如图.
1
2
3
t
y
o
20
40
60
80
100
思考1:观察“艾宾浩斯遗忘曲线”,你能发现什么规律?
t
y
o
20
40
60
80
100
1
2
3
函数的单调性
思考2:我们发现随着时间t
的增加,记忆保留量y在不
断减少;从图象上来看,
从左至右图象是在逐渐下降
的。
x
y
o
-1
x
O
y
1
1
2
4
-1
-2
1
1.从左至右图象————
2.在区间 (-∞, +∞)上,随着x的增大,f(x)的值随着 ————
2.(0,+∞)上从左至右图象上升,
当x增大时f(x)随着增大
1
上升
增大
下降
1.(-∞,0]上从左至右图象
当x增大时f(x)随着
减小
思考1:画出下列函数的图象,根据图象思考当
自变量x的值增大时,相应函数值是如何变化的?
x
y
o
-1
x
O
y
1
1
2
4
-1
-2
1
1
在某一区间内,
当x的值增大时,函数值y也增大——图象在该区间内逐渐上升;
当x的值增大时,函数值y反而减小——图象在该区间内逐渐下降。
函数的这种性质称为函数的单调性
思考2:通过上面的观察,如何用图象上动点P(x,y)的横、纵坐标的变化来说明上升或下降趋势?
思考3:如何用数学符号语言定义函数所具有的这种性质?
图象在区间D逐渐上升
区间D内随着x的增大,y也增大
x
0
1
2
1
y
方案1:在区间(0,+ )上取自变量1,2,∵1<2, f(1)
∞
方案二:
对区间D内 任意 x1,x2 ,
当x1
区间D内随着x的增大,y也增大
x
0
x1
x2
f (x1)
f (x2)
方案1:在区间(0,+ )上取自变量1,2,∵1<2, f(1)
方案3:在(0,+∞)内取任意的x1,x2 且x1
∞
∞
y
对区间D内 x1,x2 ,
当x1
设函数y=f(x)的定义域为I,区间D I.
定义
任意
如果对于区间D上的任意
两个自变量的值x1,x2,
当x1
D称为 f (x)的单调
增区间.
那么就说 f (x)在区间D上
是单调增函数,
区间D内随着x的增大,y也增大
图象在区间D逐渐上升
0
x1
f (x1)
f (x2)
1
2
1
y
那么就说在f(x)这个区间上是单调
减函数,D称为f(x)的单调 减 区间.
O
x
y
x1
x2
f(x1)
f(x2)
类比单调增函数的研究方法定义单调减函数.
x
O
y
x1
x2
f(x1)
f(x2)
设函数y=f(x)的定义域为I,区间D I.
如果对于属于定义域I内某个区间D上
的任意两个自变量的值x1,x2,
设函数y=f(x)的定义域为I,区间D I.
如果对于属于定义域I内某个区间D上
的任意两个自变量的值x1,x2,
那么就说在f(x)这个区间上是单调增 函数,D称为f(x)的单调 区间.
增
当x1
当x1
单调区间
如果函数 y =f(x)在区间D是单调增函数或单调减函数,那么就说函数 y =f(x)在区间D上具有单调性。
(1)函数单调性是针对某个区间而言的,是一个局部性质;
判断1:函数 f (x)= x2 在 是单调增函数;
x
y
o
(2) x 1, x 2 取值的任意性
判断2:定义在R上的函数
f (x)满足 f (2)> f(1),则
函数 f (x)在R上是增函数;
y
x
O
1
2
f(1)
f(2)
解:函数y=f(x)的单调区间有[-5,-2),[-2,1) ,[1,3), [3,5].
例1. 如图是定义在闭区间[-5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调区间, 以及在每一单调区间上, 函数是增函数还是减函数?
其中y=f(x)在区间[-2,1),[3,5]上是增函数;
说明:1.区间端点处若有定义写开写闭均可.
2.图象法判断函数的单调性:从左向右看图象的升降情况
在区间[-5,-2),[1,3)上是减函数.
-4
3
2
1
5
4
3
1
2
-1
-2
-1
-5
-3
-2
x
y
O
练一练
根据下图说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数.
2
5
4
4
x
y
O
-1
3
2
1
解:函数y=f(x)的单调区间有[-1,0),[0,2) ,[2,4), [4,5].
其中y=f(x)在区间[0,2),[4,5]上是增函数;
在区间[-1,0),[2,4)上是减函数.
例2 证明函数 f(x) = 3 x+2在区间R上是增函数.
例2 证明函数 f(x) = 3 x+2在区间R上是增函数.
设 x1,x2 是 R上任意两个实数,且x1﹤x2
证明:
则 f(x1) - f(x2) = (3x1+2) - (3x2+2)
= 3(x1-x2)
由 x1﹤x2 ,得 x1 - x2﹤0
于是 f(x1) - f(x2) ﹤0
即 f(x1) ﹤ f(x2)
所以 f(x)=3x+2在R上是增函数
作差
设值
变形
定号
下结论
用定义证明函数单调性的四步骤:
(1)设值:
在所给区间上任意设两个实 数
(2)作差
(3)变形
作差
:常通过“因式分解”、“通分”、“配方”等
手段将差式变形为因式乘积或平方和形式
判断 的符号
(4)结论:
并作出单调性的结论
设量
判断差符号
作差变形
下结论
课堂小结
1. 两个定义:增函数、减函数的定义;
②(定义法)证明函数单调性,步骤:
①图象法判断函数的单调性:
增函数的图象从左到右
减函数的图象从左到右
上升
下降
3.一个数学思想:数形结合
2:两种方法
例2、物理学中的玻意耳定律 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大。试用函数的单调性证明之。
证明:
1
2
3
4
1.设值;
2.作差变形;
3.定号;
4.下结论
?
画出函数 图象,写出定义域并写出单调区间:
x
y
_____________
,
讨论:根据函数单调性的定义
拓展探究
y
O
x
在 (0,+∞) 上任取 x1、 x2
当x1< x2时,都有f(x1) f(x2)
>
y
O
x
-1
1
-1
1
取自变量-1< 1,
而 f(-1) f(1)
∴不能说 在(-∞,0)∪(0,+∞)上是减函数
要写成(-∞,0),(0,+∞)的形式。
<
逗号隔开
巩固
对区间D内 任意 x1,x2 ,
当x1
区间D内随着x的增大,y也增大
x
0
x1
x2
f (x1)
f (x2)
1
2
1
方案1:在区间(0,+ )上取自变量1,2,∵1<2, f(1)
方案3:在(0,+∞)内取任意的x1,x2 且x1
∞
∞
y
