人教A版高中数学必修4第一章1.2.2同角三角函数的基本关系课件(27张PPT)
文档属性
| 名称 | 人教A版高中数学必修4第一章1.2.2同角三角函数的基本关系课件(27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 06:53:27 | ||
图片预览






文档简介
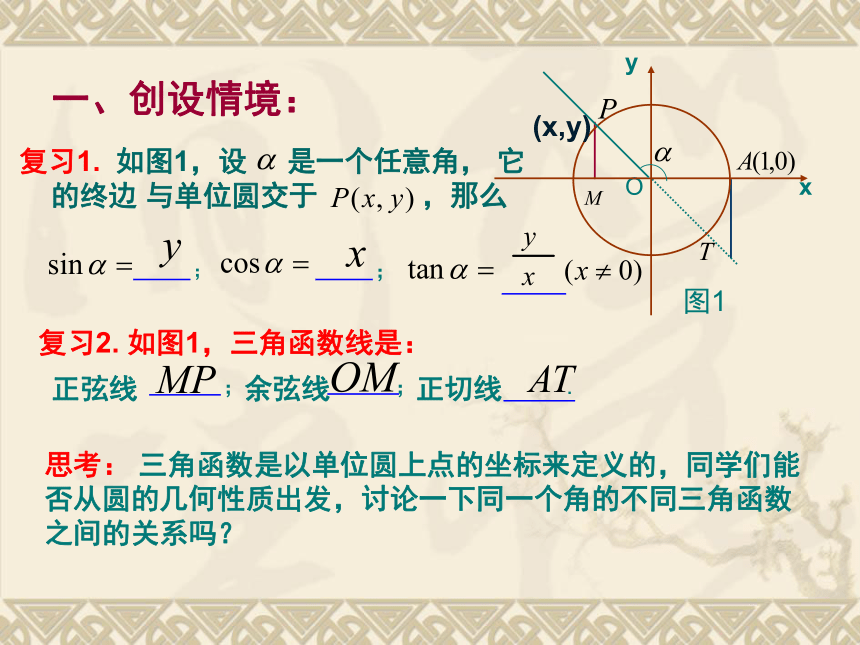
同角三角函数的基本关系式
高一数学备课组
2020.12.07
一、创设情境:
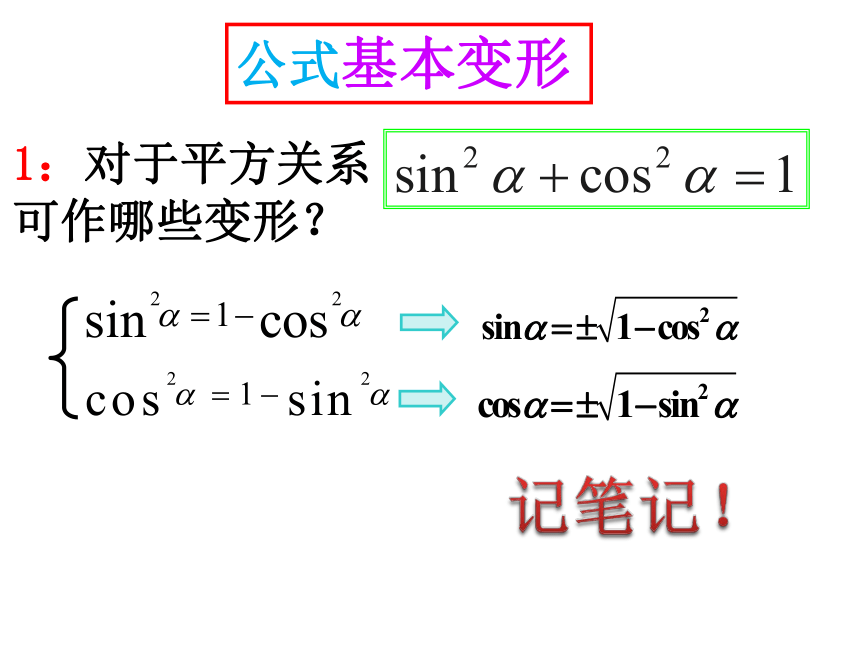
复习2. 如图1,三角函数线是:
正弦线
;
余弦线
;
正切线
.
;
;
思考: 三角函数是以单位圆上点的坐标来定义的,同学们能否从圆的几何性质出发,讨论一下同一个角的不同三角函数之间的关系吗?
复习1. 如图1,设 是一个任意角, 它的终边 与单位圆交于 ,那么
O
x
y
图1
(x,y)
二、探究新知:
思考2:当角 的终边在坐标轴上时,关系式是否还成立?
对于任意角 都有
结论:
平方关系
思考1: 当角 的终边不在坐标轴上时,正弦、余弦之间的关系是什么?(如图2 )
1、探究同角正弦、余弦之间的关系
O
x
y
图2
当角 的终边在 坐标轴上时,
当角 的终边在 坐标轴上时,
角 的正弦线 ,余弦线 ,半经 三者的长构成直角三角形,而且 ,由勾股定理得
因此 ,即
(x,y)
2.观察任意角 的三角函数的定义
商数关系
思考:
② 这两个公式的前提是“同角”, 因此
注:
①商的关系不是对任意角都成立 ,是在等式两边都有意义的情况下,等式才成立
③
(
)
2
2
2
2
sin
sin
sin
sin
sin
a
a
a
a
a
写成
的平方,不能将
的简写,读作
是
同一角的正弦、余弦的平方和等于1.
同角三角函数基本关系式
1.平方关系:
2.商数关系:
同一角的正弦、余弦的商等于这个角的正切.
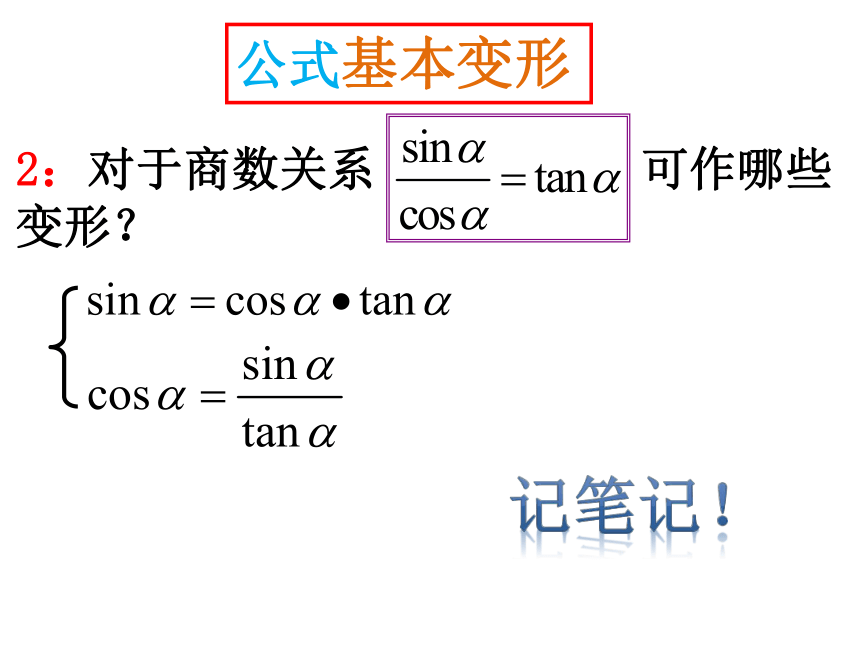
公式基本变形
1:对于平方关系 可作哪些变形?
记笔记!
2:对于商数关系 可作哪些变形?
公式基本变形
记笔记!
同角三角函数关系式的应用
(1)已知某角的一个三角函数值,
求该角的其他三角函数值.(知一求二)
(2)三角函数式的化简求值.
(3)三角恒等式的证明.明天讲
解:∵ <0 ,sina≠-1 ∴ 角 是第三或第四象限角,
②当 是第四象限角时,
① 当 是第三象限角时,
三.灵活运用
典例讲解
典例1
!!!若角所在象限不确定时,一般要
进行分类讨论
先定象限,后定值
动手做一做
1
方法1:公式变形
典例讲解
典例2.
动手做一做:化简(练习)
典例讲解
典例3.
方法2:切化弦
动手做一做
化简.
方法3:
典例讲解结合
典例4.
解:
典例5.
,分子分母同时除以cosα.
化简求值讲练结合
方法4:弦化切
动手做一做
1
弦化切:再把分子分母同时除以cos?α.
三角恒等式的证明
.
三角函数证明方法:
(2)直接法:
(证左边 右边,或右边 左边相等)
(3)左右归一法:(证得左边和右边等于相等的式子)
(4)综合法:(交叉相乘)
(1)比较法:(相减=0,相除=1)
记笔记
证法一:
因此
作差法
课本例题7
求证:
证法二:
由原题知:
则
原式左边=
=右边
因此
恒等变形的条件
证法三:
因为
因此
由原题知:
恒等变形的条件
.三角恒等式化简技巧技巧:
记笔记
证法一:
左边
右边
左边=右边
所以原等式成立
左边
中间
右边
所以原等式成立
左边 右边
证法二:
思考题:
1
请探究图中同角三角函数的关系
小结:
1. 同角三角函数基本关系式及成立的条件;
2. 求值
3.三角函数式的化简
作业
P20页第1,2,3,4
三维设计13,14 页
谢 谢!
2020.12.07
高一数学备课组
2020.12.07
一、创设情境:
复习2. 如图1,三角函数线是:
正弦线
;
余弦线
;
正切线
.
;
;
思考: 三角函数是以单位圆上点的坐标来定义的,同学们能否从圆的几何性质出发,讨论一下同一个角的不同三角函数之间的关系吗?
复习1. 如图1,设 是一个任意角, 它的终边 与单位圆交于 ,那么
O
x
y
图1
(x,y)
二、探究新知:
思考2:当角 的终边在坐标轴上时,关系式是否还成立?
对于任意角 都有
结论:
平方关系
思考1: 当角 的终边不在坐标轴上时,正弦、余弦之间的关系是什么?(如图2 )
1、探究同角正弦、余弦之间的关系
O
x
y
图2
当角 的终边在 坐标轴上时,
当角 的终边在 坐标轴上时,
角 的正弦线 ,余弦线 ,半经 三者的长构成直角三角形,而且 ,由勾股定理得
因此 ,即
(x,y)
2.观察任意角 的三角函数的定义
商数关系
思考:
② 这两个公式的前提是“同角”, 因此
注:
①商的关系不是对任意角都成立 ,是在等式两边都有意义的情况下,等式才成立
③
(
)
2
2
2
2
sin
sin
sin
sin
sin
a
a
a
a
a
写成
的平方,不能将
的简写,读作
是
同一角的正弦、余弦的平方和等于1.
同角三角函数基本关系式
1.平方关系:
2.商数关系:
同一角的正弦、余弦的商等于这个角的正切.
公式基本变形
1:对于平方关系 可作哪些变形?
记笔记!
2:对于商数关系 可作哪些变形?
公式基本变形
记笔记!
同角三角函数关系式的应用
(1)已知某角的一个三角函数值,
求该角的其他三角函数值.(知一求二)
(2)三角函数式的化简求值.
(3)三角恒等式的证明.明天讲
解:∵ <0 ,sina≠-1 ∴ 角 是第三或第四象限角,
②当 是第四象限角时,
① 当 是第三象限角时,
三.灵活运用
典例讲解
典例1
!!!若角所在象限不确定时,一般要
进行分类讨论
先定象限,后定值
动手做一做
1
方法1:公式变形
典例讲解
典例2.
动手做一做:化简(练习)
典例讲解
典例3.
方法2:切化弦
动手做一做
化简.
方法3:
典例讲解结合
典例4.
解:
典例5.
,分子分母同时除以cosα.
化简求值讲练结合
方法4:弦化切
动手做一做
1
弦化切:再把分子分母同时除以cos?α.
三角恒等式的证明
.
三角函数证明方法:
(2)直接法:
(证左边 右边,或右边 左边相等)
(3)左右归一法:(证得左边和右边等于相等的式子)
(4)综合法:(交叉相乘)
(1)比较法:(相减=0,相除=1)
记笔记
证法一:
因此
作差法
课本例题7
求证:
证法二:
由原题知:
则
原式左边=
=右边
因此
恒等变形的条件
证法三:
因为
因此
由原题知:
恒等变形的条件
.三角恒等式化简技巧技巧:
记笔记
证法一:
左边
右边
左边=右边
所以原等式成立
左边
中间
右边
所以原等式成立
左边 右边
证法二:
思考题:
1
请探究图中同角三角函数的关系
小结:
1. 同角三角函数基本关系式及成立的条件;
2. 求值
3.三角函数式的化简
作业
P20页第1,2,3,4
三维设计13,14 页
谢 谢!
2020.12.07
