2020-2021学年华师大新版九年级下册数学《第26章 二次函数》单元测试卷(Word版含解析)
文档属性
| 名称 | 2020-2021学年华师大新版九年级下册数学《第26章 二次函数》单元测试卷(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 207.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 20:15:41 | ||
图片预览




文档简介
2020-2021学年华师大新版九年级下册数学《第26章
二次函数》单元测试卷
一.选择题
1.若y=(m2+m)是二次函数,则m的值是( )
A.m=1±2
B.m=2
C.m=﹣1或m=3
D.m=3
2.开口向上,顶点坐标为(﹣9,3)的抛物线为( )
A.y=2(x﹣9)2﹣3
B.y=2(x+9)2+3
C.y=﹣2(x﹣9)2﹣3
D.y=﹣2(x+9)2+3
3.已知二次函数y=ax2+bx+c(a≠0),给出下列四个判断:(1)a>0;(2)2a+b=0;(3)b2﹣4ac>0;(4)a+b+c<0;以其中三个判断为条件,余下一个判断作结论,其中真命题的个数有( )
A.1
个
B.2
个
C.3
个
D.4
个
4.把直线y=﹣x+3沿y轴向下平移2个单位所得函数的解析式为( )
A.y=﹣3x+3
B.y=﹣x+5
C.y=﹣x+1
D.y=x+1
5.二次函数y=m2x2﹣4x+1有最小值﹣3,则m等于( )
A.1
B.﹣1
C.±1
D.±
6.形状与抛物线y=﹣x2﹣2相同,对称轴是x=﹣2,且过点(0,3)的抛物线是( )
A.y=x2+4x+3
B.y=﹣x2﹣4x+3
C.y=﹣x2+4x+3
D.y=x2+4x+3或y=﹣x2﹣4x+3
7.已知二次函数y=2x2﹣(4k+1)x+2k2﹣1的图象与x轴交于两个不同的点,则关于x的一元二次方程2x2﹣(4k+1)x+2k2﹣1=0的根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.没有实数根
D.无法确定
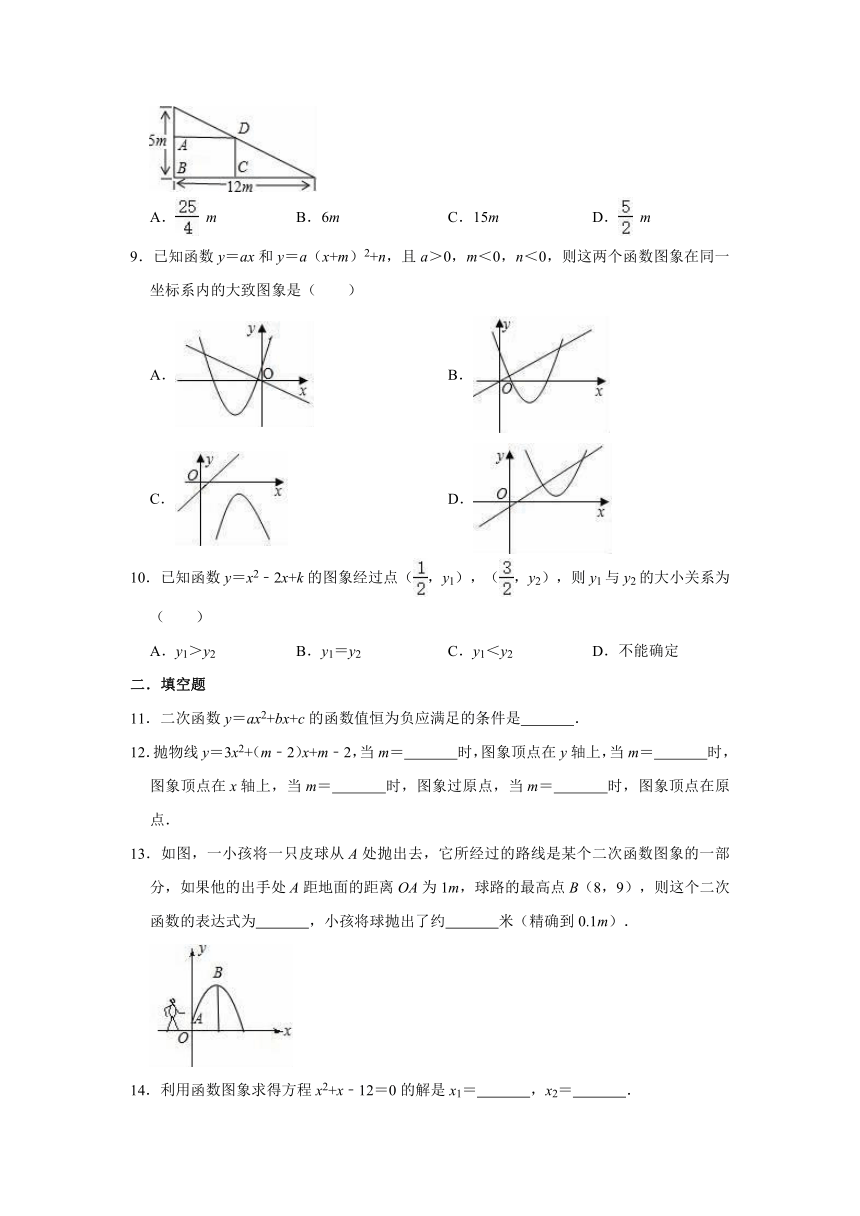
8.如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
A.
m
B.6m
C.15m
D.
m
9.已知函数y=ax和y=a(x+m)2+n,且a>0,m<0,n<0,则这两个函数图象在同一坐标系内的大致图象是( )
A.
B.
C.
D.
10.已知函数y=x2﹣2x+k的图象经过点(,y1),(,y2),则y1与y2的大小关系为( )
A.y1>y2
B.y1=y2
C.y1<y2
D.不能确定
二.填空题
11.二次函数y=ax2+bx+c的函数值恒为负应满足的条件是
.
12.抛物线y=3x2+(m﹣2)x+m﹣2,当m=
时,图象顶点在y轴上,当m=
时,图象顶点在x轴上,当m=
时,图象过原点,当m=
时,图象顶点在原点.
13.如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1m,球路的最高点B(8,9),则这个二次函数的表达式为
,小孩将球抛出了约
米(精确到0.1m).
14.利用函数图象求得方程x2+x﹣12=0的解是x1=
,x2=
.
15.将y=(2x﹣1)(x+2)+1化成y=a(x+m)2+n的形式为
.
16.已知二次函数y=ax2与一次函数y=3x﹣4的图象都过点A(b,2),则a=
.
17.m=
时,函数是二次函数.
18.抛物线y=﹣3x2的对称轴是
,顶点是
,开口
,顶点是最
点,与x轴的交点为
.
19.已知二次函数y=ax2+bx+c的图象如图所示.
(1)这个二次函数的解析式为
;
(2)这个二次函数的对称轴是
;
(3)函数y有最
值,当x=
时,y的最值为
;
(4)当x=
时,y=3.
20.抛物线y=3x2的图象向右移动两个单位,再向下移动一个单位,它的顶点坐标是
,对称轴是
,解析式是
.
三.解答题
21.试写出一个开口方向向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的表达式.
22.某果园有100棵橙子树,每一棵树均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(2)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
23.如图所示,已知抛物线y=﹣2x2﹣4x的图象E,将其向右平移两个单位后得到图象F.求图象F所表示的抛物线的解析式.
24.已知二次函数y=ax2+bx+c,当x=4时,y=3;当x=﹣1时,y=﹣8;当x=2时,y=1;求这个二次函数的解析式.
25.已知抛物线y=x2+3x﹣1.变换式子,指出抛物线的开口方向、对称轴和顶点坐标.
26.【附加题】设二次函数y=ax2+bx+c(a>0,c>1),当x=c时,y=0;当0<x<c时,y>0.请比较ac和1的大小,并说明理由.
参考答案与试题解析
一.选择题
1.解:根据题意的得:,
解得:,
∴m=3,
故选:D.
2.解:
∵抛物线顶点坐标为(﹣9,3),
∴可设抛物线解析式为y=a(x+9)2+3,
∵抛物线开口向上,
∴a>0,
故选:B.
3.解:(1)∵①a>0,
∴开口向上,
∵②2a+b=0,
∴对称轴为x=1,
∵③b2﹣4ac>0,
∴顶点在第四象限,
∴④a+b+c<0正确;
(2)∵①a>0,
∴开口向上,
∵②2a+b=0,
∴对称轴为x=1,
∵④a+b+c<0,
∴顶点在第四象限,
∴③b2﹣4ac>0正确;
(3)∵①a>0,
∴开口向上,
∵③b2﹣4ac>0,④a+b+c<0,
∴顶点在第三、四象限,
∴②2a+b=0错误;
(4)∵②2a+b=0,
∴对称轴为x=1,
∵③b2﹣4ac>0,④a+b+c<0,
∴顶点在第四象限,
∴与x轴有两个交点,
∴①a>0正确.
故选:C.
4.解:在直线y=﹣x+3上取一点(0,3),向下平移2个单位后为点(0,1),
设平移后直线解析式为y=﹣x+b,
将点(0,1)代入,得b=1.
∴得到的函数解析式为y=﹣x+1.
故选:C.
5.解:在y=m2x2﹣4x+1中,m2>0,则在顶点处取得最小值,
==﹣3,解得:m=±1.
故选:C.
6.解:设所求抛物线的函数关系式为y=ax2+bx+c,由抛物线过点(0,3),可得:c=3,
由抛物线形状与y=﹣x2﹣2相同,
分为两种情况:①开口向下,则a<0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b<0,
由此可得出B选项符合题意.
②开口向下,则a>0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b>0,
由此可得出A选项符合题意,
综合上述,符合条件的是选项D,
故选:D.
7.解:∵二次函数y=2x2﹣(4k+1)x+2k2﹣1的图象与x轴交于两个不同的点,
∴一元二次方程2x2﹣(4k+1)x+2k2﹣1=0有两个不相等的实数根.
故选:B.
8.解:根据题意得:y=30﹣(5﹣x)﹣x(12﹣),
整理得y=﹣x2+12x,
=﹣
[x2﹣5x+()2﹣],
=﹣(x﹣)2+15,
∵
∴长方形面积有最大值,此时边长x应为m.
故选:D.
9.解:由解析式y=a(x+m)2+n可知,a>0,图象开口向上,其顶点坐标为(﹣m,n),又因为m<0,n<0;所以顶点坐标在第四象限,排除A、D;
C中,由二次函数图象可知a<0,而由一次函数的图象可知a>0,两者相矛盾,排除C;选项B正确.
故选:B.
10.解:∵对称轴为x=﹣=1,
∴点(,y1)的对称点的横坐标为,即称点坐标为(,y2),
∴y1=y2.
故选:B.
二.填空题
11.解:根据题意作图如下,从图中可以看出二次函数y=ax2+bx+c的函数值恒为负的条件a<0并且b2﹣4ac<0.
故答案为a<0并且b2﹣4ac<0.
12.解:当﹣=0,即m=2时,图象顶点在y轴上;
当=0时,图象顶点在x轴上,解得m=2或m=14;
当m﹣2=0,即m=2时,图象过原点;
当m﹣2=0时,图象顶点在原点.
故答案为2,2或14,2,2.
13.解:如图,顶点B的坐标为(8,9),图象经过点A(0,1),
设抛物线的解析式为y=a(x﹣8)2+9,
把点A代入解析式得a=﹣,
因此这个二次函数的表达式为
y=﹣(x﹣8)2+9.
当y=0时,﹣
x2+2x+1=0,
解得x1≈16.5,x2=﹣0.5(不合题意,舍去);
因此小孩将球抛出了约16.5米.
故填y=﹣(x﹣8)2+9、16.5.
14.解:∵方程x2+x﹣12=0的解就是函数y=x2+x﹣12的图象与x轴的交点的横坐标,
而y=x2+x﹣12的图象如图所示:
∴y=x2+x﹣12的图象与x轴的交点坐标为(﹣4,0)、(3,0),
∴方程x2+x﹣12=0的解是x1=﹣4,x2=3.
15.解:y=(2x﹣1)(x+2)+1,
=2x2+3x﹣1,
=2(x2+x+)﹣﹣1,
=2(x+)2﹣.
16.解:把A(b,2)代入y=3x﹣4得2=3b﹣4,解得b=2,
所以A点坐标为(2,2),
把A(2,2)代入y=ax2得2=4a,解得a=.
故答案为.
17.解:根据二次函数的定义得,
解得
所以m=2.
故m=2时,函数是二次函数.
18.解:抛物线y=﹣3x2的对称轴是y轴,顶点是:(0,0),开口向下,顶点是最高点,与x轴的交点为:(0,0).
故答案为:y轴,(0,0),向下,高,(0,0).
19.解:(1)根据题意,抛物线的顶点坐标是(1,﹣1),
设抛物线的表达式为y=a(x﹣1)2﹣1,
抛物线过(0,0),
所以a﹣1=0,a=1.
y=(x﹣1)2﹣1=x2﹣2x.
(2)∵y=(x﹣1)2﹣1,
∴对称轴是直线x=1;
(3)∵a=1,
∴数y有最小值,当x=1时,y的最值为﹣1;
(4)y=3时,x2﹣2x=3,
解得x=﹣1或3,
∴当x═﹣1或3时,y=3.
故答案为y=x2﹣2x;x=1;小,1,﹣1;﹣1或3.
20.解:抛物线y=3x2的图象向右移动2个单位,再向下移动1个单位,解析式是y=3(x﹣2)2﹣1,它的顶点坐标是(2,﹣1),对称轴是直线x=2.
故答案为:(2,﹣1);x=2;y=3(x﹣2)2﹣1.
三.解答题
21.解:∵开口方向向上,
∴可令a=1,
对称轴为﹣=2,
解得b=﹣4,
∵与y轴交点坐标为(0,3),
∴c=3,
所以,抛物线表达式为y=x2﹣4x+3(答案不唯一).
22.解:(1)假设果园增种x棵橙子树,那么果园共有(x+100)棵橙子树,
∵每多种一棵树,平均每棵树就会少结5个橙子,
∴这时平均每棵树就会少结5x个橙子,
则平均每棵树结(600﹣5x)个橙子.
答:假设果园增种x棵橙子树,那么果园共有(x+100)棵橙子树,这时平均每棵树结(600﹣5x)个橙子.
(2)如果果园橙子的总产量为y,
则y=(x+100)(600﹣5x)
=﹣5x2+100x+60000.
23.解:图象E所表示的抛物线的解析式为y=﹣2x2﹣4x=﹣2(x+1)2+2,
根据平移的性质可得出图象F所表示的抛物线的解析式为y=﹣2[(x﹣2)+1]2+2=﹣2x2+4x.
24.解:根据题意,将x=4,y=3;x=﹣1,y=﹣8;x=2,y=1代入y=ax2+bx+c,
得:,
解得:,
故二次函数的解析式为:y=﹣x2+x﹣.
25.解:y=x2+3x﹣1
=﹣(x2﹣6x)﹣1,
=﹣
[(x﹣3)2﹣9]﹣1,
=﹣
[(x﹣3)2+,
∴抛物线的开口方向向上、对称轴为x=3,顶点坐标为:(3,).
26.解:当x=c时,y=0,即ac2+bc+c=0,c(ac+b+1)=0,又c>1,所以ac+b+1=0,
设一元二次方程ax2+bx+c=0两个实根为x1,x2(x1≤x2)
由,及x=c>1,得x1>0,x2>0
又因为当0<x<c时,y>0,所以x1=c,
于是二次函数y=ax2+bx+c的对称轴:即b≤﹣2ac
所以b=﹣ac﹣1≤﹣2ac即ac≤1.
二次函数》单元测试卷
一.选择题
1.若y=(m2+m)是二次函数,则m的值是( )
A.m=1±2
B.m=2
C.m=﹣1或m=3
D.m=3
2.开口向上,顶点坐标为(﹣9,3)的抛物线为( )
A.y=2(x﹣9)2﹣3
B.y=2(x+9)2+3
C.y=﹣2(x﹣9)2﹣3
D.y=﹣2(x+9)2+3
3.已知二次函数y=ax2+bx+c(a≠0),给出下列四个判断:(1)a>0;(2)2a+b=0;(3)b2﹣4ac>0;(4)a+b+c<0;以其中三个判断为条件,余下一个判断作结论,其中真命题的个数有( )
A.1
个
B.2
个
C.3
个
D.4
个
4.把直线y=﹣x+3沿y轴向下平移2个单位所得函数的解析式为( )
A.y=﹣3x+3
B.y=﹣x+5
C.y=﹣x+1
D.y=x+1
5.二次函数y=m2x2﹣4x+1有最小值﹣3,则m等于( )
A.1
B.﹣1
C.±1
D.±
6.形状与抛物线y=﹣x2﹣2相同,对称轴是x=﹣2,且过点(0,3)的抛物线是( )
A.y=x2+4x+3
B.y=﹣x2﹣4x+3
C.y=﹣x2+4x+3
D.y=x2+4x+3或y=﹣x2﹣4x+3
7.已知二次函数y=2x2﹣(4k+1)x+2k2﹣1的图象与x轴交于两个不同的点,则关于x的一元二次方程2x2﹣(4k+1)x+2k2﹣1=0的根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.没有实数根
D.无法确定
8.如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
A.
m
B.6m
C.15m
D.
m
9.已知函数y=ax和y=a(x+m)2+n,且a>0,m<0,n<0,则这两个函数图象在同一坐标系内的大致图象是( )
A.
B.
C.
D.
10.已知函数y=x2﹣2x+k的图象经过点(,y1),(,y2),则y1与y2的大小关系为( )
A.y1>y2
B.y1=y2
C.y1<y2
D.不能确定
二.填空题
11.二次函数y=ax2+bx+c的函数值恒为负应满足的条件是
.
12.抛物线y=3x2+(m﹣2)x+m﹣2,当m=
时,图象顶点在y轴上,当m=
时,图象顶点在x轴上,当m=
时,图象过原点,当m=
时,图象顶点在原点.
13.如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1m,球路的最高点B(8,9),则这个二次函数的表达式为
,小孩将球抛出了约
米(精确到0.1m).
14.利用函数图象求得方程x2+x﹣12=0的解是x1=
,x2=
.
15.将y=(2x﹣1)(x+2)+1化成y=a(x+m)2+n的形式为
.
16.已知二次函数y=ax2与一次函数y=3x﹣4的图象都过点A(b,2),则a=
.
17.m=
时,函数是二次函数.
18.抛物线y=﹣3x2的对称轴是
,顶点是
,开口
,顶点是最
点,与x轴的交点为
.
19.已知二次函数y=ax2+bx+c的图象如图所示.
(1)这个二次函数的解析式为
;
(2)这个二次函数的对称轴是
;
(3)函数y有最
值,当x=
时,y的最值为
;
(4)当x=
时,y=3.
20.抛物线y=3x2的图象向右移动两个单位,再向下移动一个单位,它的顶点坐标是
,对称轴是
,解析式是
.
三.解答题
21.试写出一个开口方向向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的表达式.
22.某果园有100棵橙子树,每一棵树均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(2)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
23.如图所示,已知抛物线y=﹣2x2﹣4x的图象E,将其向右平移两个单位后得到图象F.求图象F所表示的抛物线的解析式.
24.已知二次函数y=ax2+bx+c,当x=4时,y=3;当x=﹣1时,y=﹣8;当x=2时,y=1;求这个二次函数的解析式.
25.已知抛物线y=x2+3x﹣1.变换式子,指出抛物线的开口方向、对称轴和顶点坐标.
26.【附加题】设二次函数y=ax2+bx+c(a>0,c>1),当x=c时,y=0;当0<x<c时,y>0.请比较ac和1的大小,并说明理由.
参考答案与试题解析
一.选择题
1.解:根据题意的得:,
解得:,
∴m=3,
故选:D.
2.解:
∵抛物线顶点坐标为(﹣9,3),
∴可设抛物线解析式为y=a(x+9)2+3,
∵抛物线开口向上,
∴a>0,
故选:B.
3.解:(1)∵①a>0,
∴开口向上,
∵②2a+b=0,
∴对称轴为x=1,
∵③b2﹣4ac>0,
∴顶点在第四象限,
∴④a+b+c<0正确;
(2)∵①a>0,
∴开口向上,
∵②2a+b=0,
∴对称轴为x=1,
∵④a+b+c<0,
∴顶点在第四象限,
∴③b2﹣4ac>0正确;
(3)∵①a>0,
∴开口向上,
∵③b2﹣4ac>0,④a+b+c<0,
∴顶点在第三、四象限,
∴②2a+b=0错误;
(4)∵②2a+b=0,
∴对称轴为x=1,
∵③b2﹣4ac>0,④a+b+c<0,
∴顶点在第四象限,
∴与x轴有两个交点,
∴①a>0正确.
故选:C.
4.解:在直线y=﹣x+3上取一点(0,3),向下平移2个单位后为点(0,1),
设平移后直线解析式为y=﹣x+b,
将点(0,1)代入,得b=1.
∴得到的函数解析式为y=﹣x+1.
故选:C.
5.解:在y=m2x2﹣4x+1中,m2>0,则在顶点处取得最小值,
==﹣3,解得:m=±1.
故选:C.
6.解:设所求抛物线的函数关系式为y=ax2+bx+c,由抛物线过点(0,3),可得:c=3,
由抛物线形状与y=﹣x2﹣2相同,
分为两种情况:①开口向下,则a<0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b<0,
由此可得出B选项符合题意.
②开口向下,则a>0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b>0,
由此可得出A选项符合题意,
综合上述,符合条件的是选项D,
故选:D.
7.解:∵二次函数y=2x2﹣(4k+1)x+2k2﹣1的图象与x轴交于两个不同的点,
∴一元二次方程2x2﹣(4k+1)x+2k2﹣1=0有两个不相等的实数根.
故选:B.
8.解:根据题意得:y=30﹣(5﹣x)﹣x(12﹣),
整理得y=﹣x2+12x,
=﹣
[x2﹣5x+()2﹣],
=﹣(x﹣)2+15,
∵
∴长方形面积有最大值,此时边长x应为m.
故选:D.
9.解:由解析式y=a(x+m)2+n可知,a>0,图象开口向上,其顶点坐标为(﹣m,n),又因为m<0,n<0;所以顶点坐标在第四象限,排除A、D;
C中,由二次函数图象可知a<0,而由一次函数的图象可知a>0,两者相矛盾,排除C;选项B正确.
故选:B.
10.解:∵对称轴为x=﹣=1,
∴点(,y1)的对称点的横坐标为,即称点坐标为(,y2),
∴y1=y2.
故选:B.
二.填空题
11.解:根据题意作图如下,从图中可以看出二次函数y=ax2+bx+c的函数值恒为负的条件a<0并且b2﹣4ac<0.
故答案为a<0并且b2﹣4ac<0.
12.解:当﹣=0,即m=2时,图象顶点在y轴上;
当=0时,图象顶点在x轴上,解得m=2或m=14;
当m﹣2=0,即m=2时,图象过原点;
当m﹣2=0时,图象顶点在原点.
故答案为2,2或14,2,2.
13.解:如图,顶点B的坐标为(8,9),图象经过点A(0,1),
设抛物线的解析式为y=a(x﹣8)2+9,
把点A代入解析式得a=﹣,
因此这个二次函数的表达式为
y=﹣(x﹣8)2+9.
当y=0时,﹣
x2+2x+1=0,
解得x1≈16.5,x2=﹣0.5(不合题意,舍去);
因此小孩将球抛出了约16.5米.
故填y=﹣(x﹣8)2+9、16.5.
14.解:∵方程x2+x﹣12=0的解就是函数y=x2+x﹣12的图象与x轴的交点的横坐标,
而y=x2+x﹣12的图象如图所示:
∴y=x2+x﹣12的图象与x轴的交点坐标为(﹣4,0)、(3,0),
∴方程x2+x﹣12=0的解是x1=﹣4,x2=3.
15.解:y=(2x﹣1)(x+2)+1,
=2x2+3x﹣1,
=2(x2+x+)﹣﹣1,
=2(x+)2﹣.
16.解:把A(b,2)代入y=3x﹣4得2=3b﹣4,解得b=2,
所以A点坐标为(2,2),
把A(2,2)代入y=ax2得2=4a,解得a=.
故答案为.
17.解:根据二次函数的定义得,
解得
所以m=2.
故m=2时,函数是二次函数.
18.解:抛物线y=﹣3x2的对称轴是y轴,顶点是:(0,0),开口向下,顶点是最高点,与x轴的交点为:(0,0).
故答案为:y轴,(0,0),向下,高,(0,0).
19.解:(1)根据题意,抛物线的顶点坐标是(1,﹣1),
设抛物线的表达式为y=a(x﹣1)2﹣1,
抛物线过(0,0),
所以a﹣1=0,a=1.
y=(x﹣1)2﹣1=x2﹣2x.
(2)∵y=(x﹣1)2﹣1,
∴对称轴是直线x=1;
(3)∵a=1,
∴数y有最小值,当x=1时,y的最值为﹣1;
(4)y=3时,x2﹣2x=3,
解得x=﹣1或3,
∴当x═﹣1或3时,y=3.
故答案为y=x2﹣2x;x=1;小,1,﹣1;﹣1或3.
20.解:抛物线y=3x2的图象向右移动2个单位,再向下移动1个单位,解析式是y=3(x﹣2)2﹣1,它的顶点坐标是(2,﹣1),对称轴是直线x=2.
故答案为:(2,﹣1);x=2;y=3(x﹣2)2﹣1.
三.解答题
21.解:∵开口方向向上,
∴可令a=1,
对称轴为﹣=2,
解得b=﹣4,
∵与y轴交点坐标为(0,3),
∴c=3,
所以,抛物线表达式为y=x2﹣4x+3(答案不唯一).
22.解:(1)假设果园增种x棵橙子树,那么果园共有(x+100)棵橙子树,
∵每多种一棵树,平均每棵树就会少结5个橙子,
∴这时平均每棵树就会少结5x个橙子,
则平均每棵树结(600﹣5x)个橙子.
答:假设果园增种x棵橙子树,那么果园共有(x+100)棵橙子树,这时平均每棵树结(600﹣5x)个橙子.
(2)如果果园橙子的总产量为y,
则y=(x+100)(600﹣5x)
=﹣5x2+100x+60000.
23.解:图象E所表示的抛物线的解析式为y=﹣2x2﹣4x=﹣2(x+1)2+2,
根据平移的性质可得出图象F所表示的抛物线的解析式为y=﹣2[(x﹣2)+1]2+2=﹣2x2+4x.
24.解:根据题意,将x=4,y=3;x=﹣1,y=﹣8;x=2,y=1代入y=ax2+bx+c,
得:,
解得:,
故二次函数的解析式为:y=﹣x2+x﹣.
25.解:y=x2+3x﹣1
=﹣(x2﹣6x)﹣1,
=﹣
[(x﹣3)2﹣9]﹣1,
=﹣
[(x﹣3)2+,
∴抛物线的开口方向向上、对称轴为x=3,顶点坐标为:(3,).
26.解:当x=c时,y=0,即ac2+bc+c=0,c(ac+b+1)=0,又c>1,所以ac+b+1=0,
设一元二次方程ax2+bx+c=0两个实根为x1,x2(x1≤x2)
由,及x=c>1,得x1>0,x2>0
又因为当0<x<c时,y>0,所以x1=c,
于是二次函数y=ax2+bx+c的对称轴:即b≤﹣2ac
所以b=﹣ac﹣1≤﹣2ac即ac≤1.
