人教版 九年级数学上册 第25章 概率初步 同步课时训练 (Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学上册 第25章 概率初步 同步课时训练 (Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:00:00 | ||
图片预览




文档简介
人教版 九年级数学 第25章 概率初步 同步课时训练
一、选择题
1. 下列事件中,属于必然事件的是( )
A.掷一枚硬币,正面朝上
B.抛出的篮球会下落
C.任意的三条线段可以组成三角形
D.同位角相等
2. 在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
3. 如图是一个可以自由转动的转盘,该转盘被平均分为8份,每份对应一种颜色,转动这个转盘,转出哪种颜色的可能性最小( )
A.红色 B.黄色 C.绿色 D.不确定
4. 一个布袋里装有2个红球、3个黄球和5个白球,这些球除颜色不同外其他都相同.搅匀后任意摸出1个球,是白球的概率为( )
A. B. C. D.
5. 下列事件发生的概率为0的是( )
A.射击运动员只射击1次,就命中靶心
B.任取一个实数x,都有|x|≥0
C.画一个三角形,使其三边的长分别为8 cm,6 cm,2 cm
D.抛掷一枚质地均匀且六个面上分别刻有1到6的点数的正方体骰子,朝上一面的点数为6
6. 如图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.
下面有三个推断:①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟此试验,则当投掷次数为1000时,“钉尖向上”的频率一定是0.620.其中合理的是( )
A.① B.② C.①② D.①③
7. 2019·毕节 在平行四边形ABCD中,AC,BD是两条对角线,现从以下四个关系:①AB=BC;②AC=BD;③AC⊥BD;④AB⊥BC中随机取出一个作为条件,能推出平行四边形ABCD是菱形的概率为( )
A. B. C. D.1
8. 如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=13,AC=5,BC=12,阴影部分是△ABC的内切圆.一只自由飞翔的小鸟随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
A.π B.π C.π D.
二、填空题
9. 如图,把图中能自由转动的转盘的序号按转出黑色(阴影)的可能性从小到大的顺序排列起来是____________.
10. 用力旋转涂有红、黄、蓝、白四色的转盘,指针停在红色上,是________事件,举一个和它事件类型不一样的事件:________________________________________________.
11. 一个不透明的口袋中有四个完全相同的小球,其上分别标有数字1,2,4,8.随机摸取一个小球后不放回,再随机摸取一个小球,则两次取出的小球上数字之积等于8的概率是________.
12. “抛掷一枚质地均匀的硬币,正面向上”是______事件(从“必然”“随机”“不可能”中选一个).
13. 如图所示的圆面图案是用半径相同的圆与圆弧构成的.若向圆面投掷飞镖,则飞镖落在阴影区域的概率为________.
14. 点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是________.
15. 如图,这是一幅长为3 m,宽为2 m的长方形世界杯宣传画,为测量宣传画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在世界杯图案中的频率稳定在常数0.4附近,由此可估计宣传画上世界杯图案的面积为________m2.
16. 任取不等式组的一个整数解,则能使关于x的方程2x+k=-1的解为非负数的概率为________.
三、解答题
17. 某校九年级学生共900人,为了解这个年级学生的体能,从中随机抽取部分学生进行1 min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理.下面是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;
丁:第②、③、④组的频数之比为4∶17∶15.
根据这四名同学提供的材料,请解答如下问题:
(1)这次跳绳测试共抽取多少名学生?各组有多少人?
(2)如果跳绳次数不少于135次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为多少?
(3)以每组的组中值(每组的中点对应的数据)作为这组跳绳次数的代表,估计这批学生1 min跳绳次数的平均值.
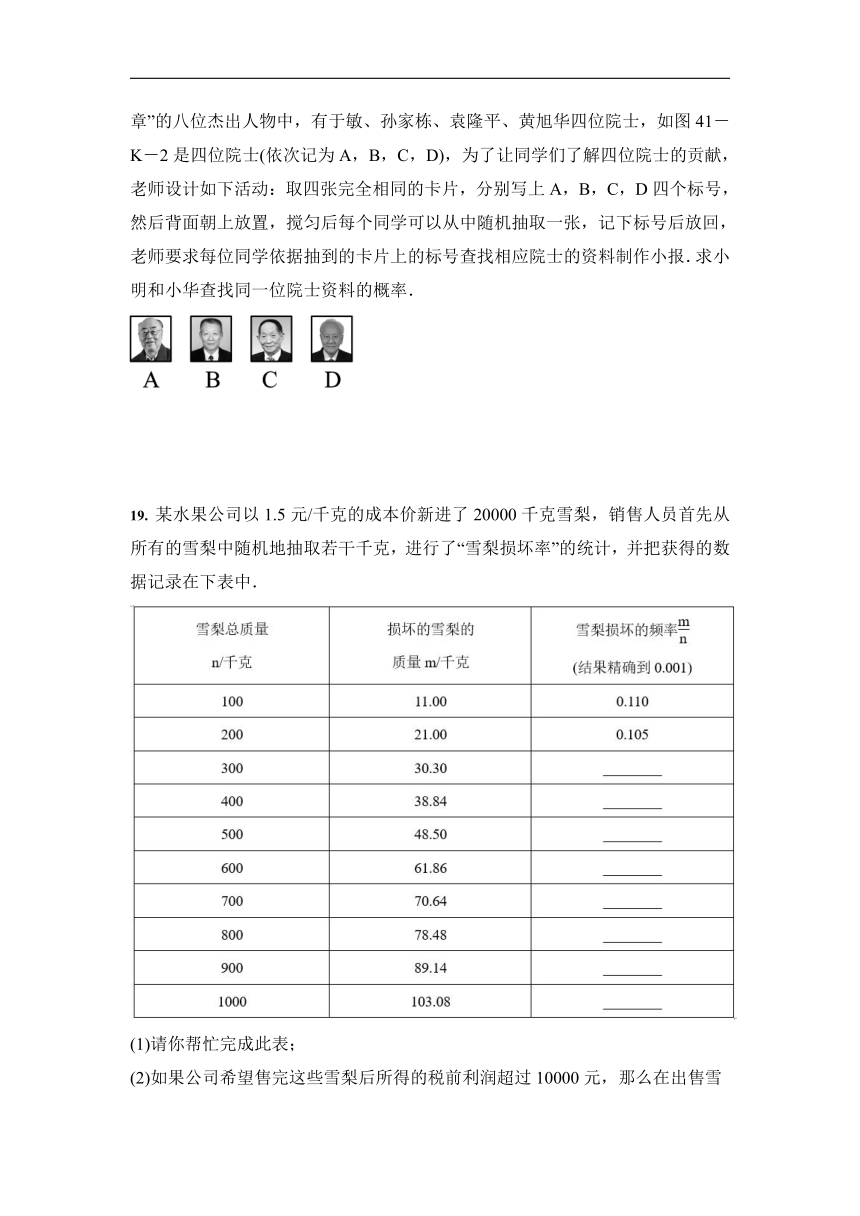
18. “共和国勋章”是中华人民共和国的最高荣誉勋章,在2019年获得“共和国勋章”的八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士,如图41-K-2是四位院士(依次记为A,B,C,D),为了让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上A,B,C,D四个标号,然后背面朝上放置,搅匀后每个同学可以从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料制作小报.求小明和小华查找同一位院士资料的概率.
19. 某水果公司以1.5元/千克的成本价新进了20000千克雪梨,销售人员首先从所有的雪梨中随机地抽取若干千克,进行了“雪梨损坏率”的统计,并把获得的数据记录在下表中.
(1)请你帮忙完成此表;
(2)如果公司希望售完这些雪梨后所得的税前利润超过10000元,那么在出售雪梨(已去掉损坏的雪梨)时,售价最低应定为多少元/千克(结果精确到0.1元/千克)?
20. 在一个不透明的袋子里装有4个分别标有1,2,3,4的小球,它们的形状、大小等完全相同.李强从袋子里随机取出1个小球,记下数字为x,王芳在剩下的3个小球中随机取出1个小球,记下数字为y,这样就确定了点M的坐标(x,y).
(1)画树状图或列表,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=x+1的图象上的概率.
人教版 九年级数学 第25章 概率初步 同步课时训练 -答案
一、选择题
1. 【答案】B
2. 【答案】D
3. 【答案】B
4. 【答案】A
5. 【答案】C [解析] 选项A是随机事件,概率在0到1之间;选项B是一个必然事件,概率为1;选项C是一个不可能事件,概率为0;选项D是一个随机事件,概率为.
6. 【答案】B
7. 【答案】B
8. 【答案】B [解析] 因为132=122+52,即AB2=BC2+AC2,所以△ABC为直角三角形,
所以△ABC的内切圆半径=×(12+5-13)=2.
所以S△ABC=AC·BC=×12×5=30,S圆=4π.
所以小鸟落在花圃上的概率===π.
故选B.
二、填空题
9. 【答案】⑤③②④① [解析] 黑色部分多的转出黑色的可能性较大,故图中能自由转动的转盘的序号按转出黑色的可能性从小到大的顺序排列起来是⑤③②④①.
10. 【答案】随机 答案不唯一,如用力旋转涂有红、黄、蓝、白四色的转盘,指针停在黑色上,是不可能事件
11. 【答案】 [解析] 本题考查了用列举法求概率,关键扣住“不放回”,用列表法列出等可能的结果如下:
所以共有12种等可能的结果,其中两次取出的小球上数字之积等于8的结果有4种,所以P(两次取出的小球上数字之积等于8)==.
12. 【答案】随机 [解析] 事件“抛掷一枚质地均匀的硬币,正面向上”可能发生,也可能不发生,因此是随机事件.
13. 【答案】
14. 【答案】 [解析] 画树状图如下:
共有20种等可能的结果,其中点P(a,b)在平面直角坐标系中第二象限内的结果有4种,
所以点P(a,b)在平面直角坐标系中第二象限内的概率为=.
15. 【答案】2.4 [解析] 大量重复试验中,当频率稳定在常数0.4附近时,可估计概率为0.4,所以图案的面积≈3×2×0.4=2.4(m2).
16. 【答案】 [解析] 因为不等式组的解集为-<k≤3,
所以不等式组的整数解为-2,-1,0,1,2,3.
关于x的方程2x+k=-1的解为x=-.
因为关于x的方程2x+k=-1的解为非负数,
所以k+1≤0,解得k≤-1,
所以能使关于x的方程2x+k=-1的解为非负数的k的值为-1,-2,
所以能使关于x的方程2x+k=-1的解为非负数的概率为=.
三、解答题
17. 【答案】
解:(1)第①组频率为1-96%=0.04.
∴第②组频率为0.12-0.04=0.08,
从而,总人数为12÷0.08=150人.
又②③④组的频数之比为4∶17∶15,可算得第①~⑥组的人数分别为6、12、51、45、24、12.
(2)第⑤、⑥两组的频率之和为0.16+0.08=0.24.由样本是随机抽取的,估计全年级有900×0.24=216人达到优秀.
(3)x=
=127(次).
18. 【答案】
解:根据题意画树状图如下:
共有16种等可能的结果,其中小明和小华查找同一位院士资料的结果有4种,所以小明和小华查找同一位院士资料的概率为=.
19. 【答案】
解:(1)表中从上到下依次填:0.101,0.097,0.097,0.103,0.101,0.098,0.099,0.103.
(2)填完表后,从表中可以看出,雪梨损坏的频率在常数0.1左右摆动,并且随统计量的增加,这种规律逐渐明显,那么可以估计雪梨损坏的概率为0.1,
则在20000千克雪梨中完好的雪梨的质量约为20000×(1-0.1)=18000(千克),完好的雪梨的实际进价为=(元/千克).
设雪梨的售价为x元/千克,则有
×18000>10000,解得x>2.2.
故在出售雪梨时,售价最低应定为2.3元/千克.
20. 【答案】
解:(1)画树状图如下:
由图可知,点M的坐标共有12种,即(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3).
(2)以上12个点中,在函数y=x+1的图象上的点有3个,
即(1,2),(2,3),(3,4),
所以所求概率==.
一、选择题
1. 下列事件中,属于必然事件的是( )
A.掷一枚硬币,正面朝上
B.抛出的篮球会下落
C.任意的三条线段可以组成三角形
D.同位角相等
2. 在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
3. 如图是一个可以自由转动的转盘,该转盘被平均分为8份,每份对应一种颜色,转动这个转盘,转出哪种颜色的可能性最小( )
A.红色 B.黄色 C.绿色 D.不确定
4. 一个布袋里装有2个红球、3个黄球和5个白球,这些球除颜色不同外其他都相同.搅匀后任意摸出1个球,是白球的概率为( )
A. B. C. D.
5. 下列事件发生的概率为0的是( )
A.射击运动员只射击1次,就命中靶心
B.任取一个实数x,都有|x|≥0
C.画一个三角形,使其三边的长分别为8 cm,6 cm,2 cm
D.抛掷一枚质地均匀且六个面上分别刻有1到6的点数的正方体骰子,朝上一面的点数为6
6. 如图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.
下面有三个推断:①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟此试验,则当投掷次数为1000时,“钉尖向上”的频率一定是0.620.其中合理的是( )
A.① B.② C.①② D.①③
7. 2019·毕节 在平行四边形ABCD中,AC,BD是两条对角线,现从以下四个关系:①AB=BC;②AC=BD;③AC⊥BD;④AB⊥BC中随机取出一个作为条件,能推出平行四边形ABCD是菱形的概率为( )
A. B. C. D.1
8. 如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=13,AC=5,BC=12,阴影部分是△ABC的内切圆.一只自由飞翔的小鸟随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
A.π B.π C.π D.
二、填空题
9. 如图,把图中能自由转动的转盘的序号按转出黑色(阴影)的可能性从小到大的顺序排列起来是____________.
10. 用力旋转涂有红、黄、蓝、白四色的转盘,指针停在红色上,是________事件,举一个和它事件类型不一样的事件:________________________________________________.
11. 一个不透明的口袋中有四个完全相同的小球,其上分别标有数字1,2,4,8.随机摸取一个小球后不放回,再随机摸取一个小球,则两次取出的小球上数字之积等于8的概率是________.
12. “抛掷一枚质地均匀的硬币,正面向上”是______事件(从“必然”“随机”“不可能”中选一个).
13. 如图所示的圆面图案是用半径相同的圆与圆弧构成的.若向圆面投掷飞镖,则飞镖落在阴影区域的概率为________.
14. 点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是________.
15. 如图,这是一幅长为3 m,宽为2 m的长方形世界杯宣传画,为测量宣传画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在世界杯图案中的频率稳定在常数0.4附近,由此可估计宣传画上世界杯图案的面积为________m2.
16. 任取不等式组的一个整数解,则能使关于x的方程2x+k=-1的解为非负数的概率为________.
三、解答题
17. 某校九年级学生共900人,为了解这个年级学生的体能,从中随机抽取部分学生进行1 min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理.下面是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;
丁:第②、③、④组的频数之比为4∶17∶15.
根据这四名同学提供的材料,请解答如下问题:
(1)这次跳绳测试共抽取多少名学生?各组有多少人?
(2)如果跳绳次数不少于135次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为多少?
(3)以每组的组中值(每组的中点对应的数据)作为这组跳绳次数的代表,估计这批学生1 min跳绳次数的平均值.
18. “共和国勋章”是中华人民共和国的最高荣誉勋章,在2019年获得“共和国勋章”的八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士,如图41-K-2是四位院士(依次记为A,B,C,D),为了让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上A,B,C,D四个标号,然后背面朝上放置,搅匀后每个同学可以从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料制作小报.求小明和小华查找同一位院士资料的概率.
19. 某水果公司以1.5元/千克的成本价新进了20000千克雪梨,销售人员首先从所有的雪梨中随机地抽取若干千克,进行了“雪梨损坏率”的统计,并把获得的数据记录在下表中.
(1)请你帮忙完成此表;
(2)如果公司希望售完这些雪梨后所得的税前利润超过10000元,那么在出售雪梨(已去掉损坏的雪梨)时,售价最低应定为多少元/千克(结果精确到0.1元/千克)?
20. 在一个不透明的袋子里装有4个分别标有1,2,3,4的小球,它们的形状、大小等完全相同.李强从袋子里随机取出1个小球,记下数字为x,王芳在剩下的3个小球中随机取出1个小球,记下数字为y,这样就确定了点M的坐标(x,y).
(1)画树状图或列表,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=x+1的图象上的概率.
人教版 九年级数学 第25章 概率初步 同步课时训练 -答案
一、选择题
1. 【答案】B
2. 【答案】D
3. 【答案】B
4. 【答案】A
5. 【答案】C [解析] 选项A是随机事件,概率在0到1之间;选项B是一个必然事件,概率为1;选项C是一个不可能事件,概率为0;选项D是一个随机事件,概率为.
6. 【答案】B
7. 【答案】B
8. 【答案】B [解析] 因为132=122+52,即AB2=BC2+AC2,所以△ABC为直角三角形,
所以△ABC的内切圆半径=×(12+5-13)=2.
所以S△ABC=AC·BC=×12×5=30,S圆=4π.
所以小鸟落在花圃上的概率===π.
故选B.
二、填空题
9. 【答案】⑤③②④① [解析] 黑色部分多的转出黑色的可能性较大,故图中能自由转动的转盘的序号按转出黑色的可能性从小到大的顺序排列起来是⑤③②④①.
10. 【答案】随机 答案不唯一,如用力旋转涂有红、黄、蓝、白四色的转盘,指针停在黑色上,是不可能事件
11. 【答案】 [解析] 本题考查了用列举法求概率,关键扣住“不放回”,用列表法列出等可能的结果如下:
所以共有12种等可能的结果,其中两次取出的小球上数字之积等于8的结果有4种,所以P(两次取出的小球上数字之积等于8)==.
12. 【答案】随机 [解析] 事件“抛掷一枚质地均匀的硬币,正面向上”可能发生,也可能不发生,因此是随机事件.
13. 【答案】
14. 【答案】 [解析] 画树状图如下:
共有20种等可能的结果,其中点P(a,b)在平面直角坐标系中第二象限内的结果有4种,
所以点P(a,b)在平面直角坐标系中第二象限内的概率为=.
15. 【答案】2.4 [解析] 大量重复试验中,当频率稳定在常数0.4附近时,可估计概率为0.4,所以图案的面积≈3×2×0.4=2.4(m2).
16. 【答案】 [解析] 因为不等式组的解集为-<k≤3,
所以不等式组的整数解为-2,-1,0,1,2,3.
关于x的方程2x+k=-1的解为x=-.
因为关于x的方程2x+k=-1的解为非负数,
所以k+1≤0,解得k≤-1,
所以能使关于x的方程2x+k=-1的解为非负数的k的值为-1,-2,
所以能使关于x的方程2x+k=-1的解为非负数的概率为=.
三、解答题
17. 【答案】
解:(1)第①组频率为1-96%=0.04.
∴第②组频率为0.12-0.04=0.08,
从而,总人数为12÷0.08=150人.
又②③④组的频数之比为4∶17∶15,可算得第①~⑥组的人数分别为6、12、51、45、24、12.
(2)第⑤、⑥两组的频率之和为0.16+0.08=0.24.由样本是随机抽取的,估计全年级有900×0.24=216人达到优秀.
(3)x=
=127(次).
18. 【答案】
解:根据题意画树状图如下:
共有16种等可能的结果,其中小明和小华查找同一位院士资料的结果有4种,所以小明和小华查找同一位院士资料的概率为=.
19. 【答案】
解:(1)表中从上到下依次填:0.101,0.097,0.097,0.103,0.101,0.098,0.099,0.103.
(2)填完表后,从表中可以看出,雪梨损坏的频率在常数0.1左右摆动,并且随统计量的增加,这种规律逐渐明显,那么可以估计雪梨损坏的概率为0.1,
则在20000千克雪梨中完好的雪梨的质量约为20000×(1-0.1)=18000(千克),完好的雪梨的实际进价为=(元/千克).
设雪梨的售价为x元/千克,则有
×18000>10000,解得x>2.2.
故在出售雪梨时,售价最低应定为2.3元/千克.
20. 【答案】
解:(1)画树状图如下:
由图可知,点M的坐标共有12种,即(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3).
(2)以上12个点中,在函数y=x+1的图象上的点有3个,
即(1,2),(2,3),(3,4),
所以所求概率==.
同课章节目录
