2020年 华东师大版八年级上数学课件12.3 乘法公式(第1课时)两数和乘以这两数的差 (18张PPT)
文档属性
| 名称 | 2020年 华东师大版八年级上数学课件12.3 乘法公式(第1课时)两数和乘以这两数的差 (18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 318.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 22:48:51 | ||
图片预览




文档简介
12.3 乘法公式
第1课时 两数和乘以这两数的差
九江一中 数学组
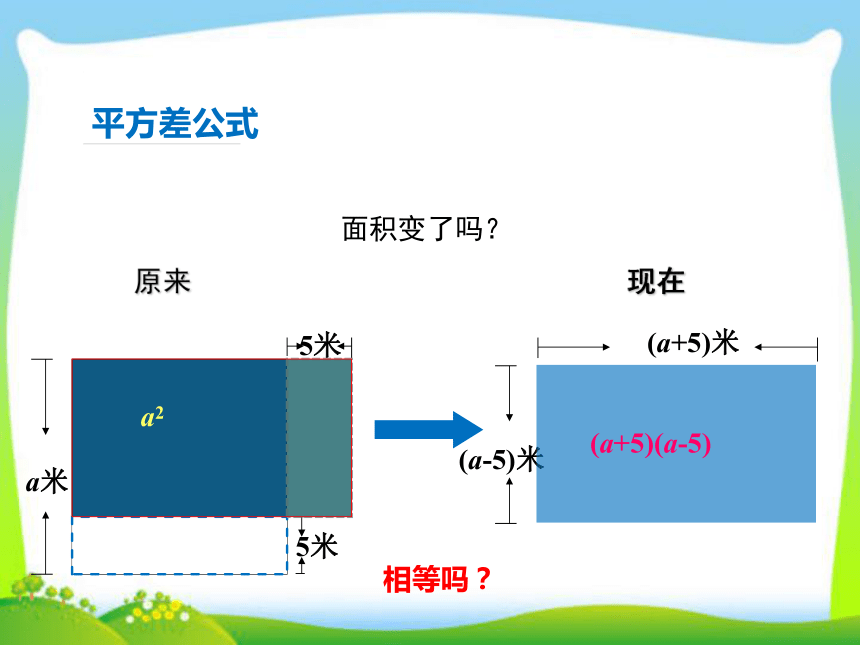
平方差公式
5米
5米
a米
(a-5)米
(a+5)米
相等吗?
原来
现在
a2
(a+5)(a-5)
面积变了吗?
(1)(x + 1)( x-1);
(2)(m + 2)( m-2);
(3)(2m+ 1)(2m-1);
(4)(5y + z)(5y-z).
计算下列多项式的积,你能发现什么规律?
x2 - 12
m2-22
(2m)2 - 12
(5y)2 - z2
【想一想】这些计算结果有什么特点?
(a+b)(a?b)=
a2?b2
这就是说,两数和与这两数差的积,等于这
两数的平方差.
这个公式叫做两数和与这两数差的乘法公式,
有时也简称为平方差公式.
1.(a – b ) ( a + b) = a2 - b2
2.(b + a )( -b + a ) = a2 - b2
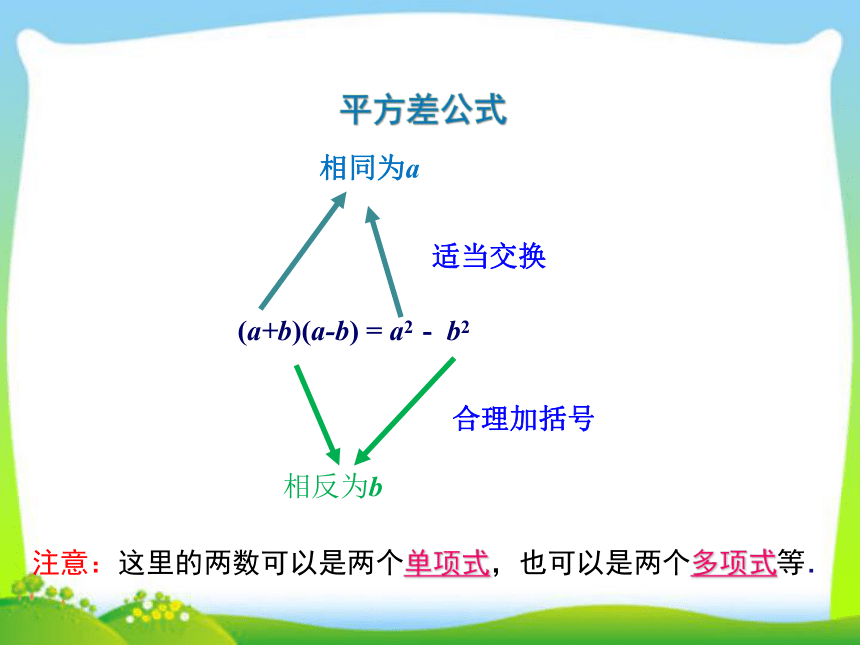
平方差公式
公式变形
=
-
(a+b)(a-b)
a2
b2
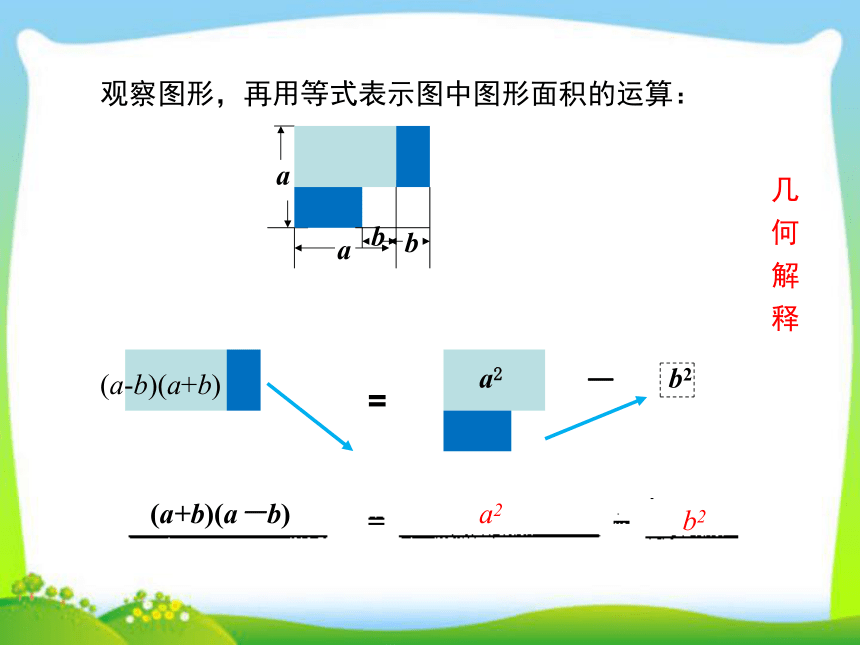
几 何 解 释
b2
a
a
b
b
(a-b)(a+b)
a2
观察图形,再用等式表示图中图形面积的运算:
平方差公式
注意:这里的两数可以是两个单项式,也可以是两个多项式等.
(a+b)(a-b) = a2 - b2
相同为a
相反为b
适当交换
合理加括号
【练一练】口答下列各题:
(l)(-a+b)(a+b)=??_________;
(2)(a-b)(b+a)= __________;
(3)(-a-b)(-a+b)= ________;
(4)(a-b)(-a-b)= _________.
a2-b2
a2-b2
b2-a2
b2-a2
【例1】 填一填:
12-x2
(-3+a)(-3-a)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(a-b)(a+b)
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
(1+x)(1-x)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
【例2】 计算:1998×2002.
1998
2002 =
(2000-2)×(2000+2)
=4 000 000-4
=3 999 996.
解:
【例3 】街心花园有一块边长为a米的正方形草坪,经统一规划后, 南北向要加长2米,而东西向要缩短2米,问改造后的长方形草坪的面积是多少?
解:
即改造后的长方形草坪的
面积是(a2-4)平方米.
1.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2)=x2-2
(2)(-3a-2)(3a-2)=9a2-4
不对
改正:
(x+2)(x-2)=x2-4 .
不对
改正一:
(-3a-2)(3a-2)=-[(3a+2)(3a-2)]
=-(9a2-4)
=-9a2+4.
改正二:
(-3a-2)(3a-2)=(-2-3a)(-2+3a)
=(-2)2-(3a)2
=4-9a2.
(1)(a+3b)(a- 3b);
=4a2-9.
=4x4-y2.
解:原式=(2a+3)(2a-3)
=a2-9b2 .
=(2a)2-32
解:原式=(-2x2 )2-y2
解:原式=(50+1)×(50-1)
=502-12
=2500-1
=2499.
解:原式=(9x2-16)
-(6x2+5x -6)
=3x2-5x- 10.
解:原式=a2-(3b)2
(2)(3+2a)(-3+2a);
(3)51×49;
(5)(3x+4)(3x-4)-(2x+3)(3x-2).
(4)(-2x2-y)(-2x2+y);
2.利用平方差公式计算:
3.计算: 20172 - 2016×2018.
解:
20172 - 2016×2018
= 20172 - (2017-1)×(2017+1)
= 20172
- (20172-12 )
= 20172
- 20172+12
=1.
4.利用平方差公式计算:
(1)(a-2)(a+2)(a2 + 4);
解:原式=(a2-4)(a2+4)
=a4-16.
(2)(x-y)(x+y)(x2+y2)(x4+y4).
解:原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
平方差公式
内 容
注 意
两数和与这两数差的积,等于这两数的平方差.
符号表示:(a+b)(a-b)=a2-b2
(1)紧紧抓住 “一同一反”
这一特征;
(2)在应用时,只有两个二
项式的积才有可能应用
平方差公式;
(3)对于不能直接应用公式
的,可能要经过变形才
可以应用
课堂总结
第1课时 两数和乘以这两数的差
九江一中 数学组
平方差公式
5米
5米
a米
(a-5)米
(a+5)米
相等吗?
原来
现在
a2
(a+5)(a-5)
面积变了吗?
(1)(x + 1)( x-1);
(2)(m + 2)( m-2);
(3)(2m+ 1)(2m-1);
(4)(5y + z)(5y-z).
计算下列多项式的积,你能发现什么规律?
x2 - 12
m2-22
(2m)2 - 12
(5y)2 - z2
【想一想】这些计算结果有什么特点?
(a+b)(a?b)=
a2?b2
这就是说,两数和与这两数差的积,等于这
两数的平方差.
这个公式叫做两数和与这两数差的乘法公式,
有时也简称为平方差公式.
1.(a – b ) ( a + b) = a2 - b2
2.(b + a )( -b + a ) = a2 - b2
平方差公式
公式变形
=
-
(a+b)(a-b)
a2
b2
几 何 解 释
b2
a
a
b
b
(a-b)(a+b)
a2
观察图形,再用等式表示图中图形面积的运算:
平方差公式
注意:这里的两数可以是两个单项式,也可以是两个多项式等.
(a+b)(a-b) = a2 - b2
相同为a
相反为b
适当交换
合理加括号
【练一练】口答下列各题:
(l)(-a+b)(a+b)=??_________;
(2)(a-b)(b+a)= __________;
(3)(-a-b)(-a+b)= ________;
(4)(a-b)(-a-b)= _________.
a2-b2
a2-b2
b2-a2
b2-a2
【例1】 填一填:
12-x2
(-3+a)(-3-a)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(a-b)(a+b)
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
(1+x)(1-x)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
【例2】 计算:1998×2002.
1998
2002 =
(2000-2)×(2000+2)
=4 000 000-4
=3 999 996.
解:
【例3 】街心花园有一块边长为a米的正方形草坪,经统一规划后, 南北向要加长2米,而东西向要缩短2米,问改造后的长方形草坪的面积是多少?
解:
即改造后的长方形草坪的
面积是(a2-4)平方米.
1.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2)=x2-2
(2)(-3a-2)(3a-2)=9a2-4
不对
改正:
(x+2)(x-2)=x2-4 .
不对
改正一:
(-3a-2)(3a-2)=-[(3a+2)(3a-2)]
=-(9a2-4)
=-9a2+4.
改正二:
(-3a-2)(3a-2)=(-2-3a)(-2+3a)
=(-2)2-(3a)2
=4-9a2.
(1)(a+3b)(a- 3b);
=4a2-9.
=4x4-y2.
解:原式=(2a+3)(2a-3)
=a2-9b2 .
=(2a)2-32
解:原式=(-2x2 )2-y2
解:原式=(50+1)×(50-1)
=502-12
=2500-1
=2499.
解:原式=(9x2-16)
-(6x2+5x -6)
=3x2-5x- 10.
解:原式=a2-(3b)2
(2)(3+2a)(-3+2a);
(3)51×49;
(5)(3x+4)(3x-4)-(2x+3)(3x-2).
(4)(-2x2-y)(-2x2+y);
2.利用平方差公式计算:
3.计算: 20172 - 2016×2018.
解:
20172 - 2016×2018
= 20172 - (2017-1)×(2017+1)
= 20172
- (20172-12 )
= 20172
- 20172+12
=1.
4.利用平方差公式计算:
(1)(a-2)(a+2)(a2 + 4);
解:原式=(a2-4)(a2+4)
=a4-16.
(2)(x-y)(x+y)(x2+y2)(x4+y4).
解:原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
平方差公式
内 容
注 意
两数和与这两数差的积,等于这两数的平方差.
符号表示:(a+b)(a-b)=a2-b2
(1)紧紧抓住 “一同一反”
这一特征;
(2)在应用时,只有两个二
项式的积才有可能应用
平方差公式;
(3)对于不能直接应用公式
的,可能要经过变形才
可以应用
课堂总结
