2020年华东师大版八年级上册数学课件 12.2 整式的乘法(第2课时)单项式与多项式相乘(15张PPT)
文档属性
| 名称 | 2020年华东师大版八年级上册数学课件 12.2 整式的乘法(第2课时)单项式与多项式相乘(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 436.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:00:00 | ||
图片预览




文档简介
12.2 整式的乘法
第2课时 单项式与多项式相乘
九江一中 数学组
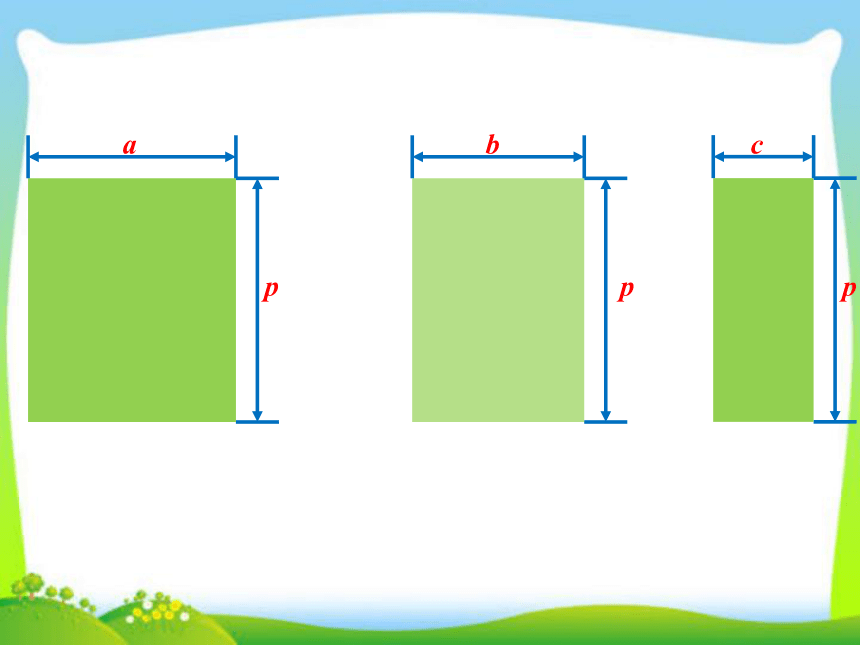
把它们看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
p
p
a
b
p
c
pa
pc
pb
单项式与多项式相乘
p
p
a
b
p
c
c
b
a
p
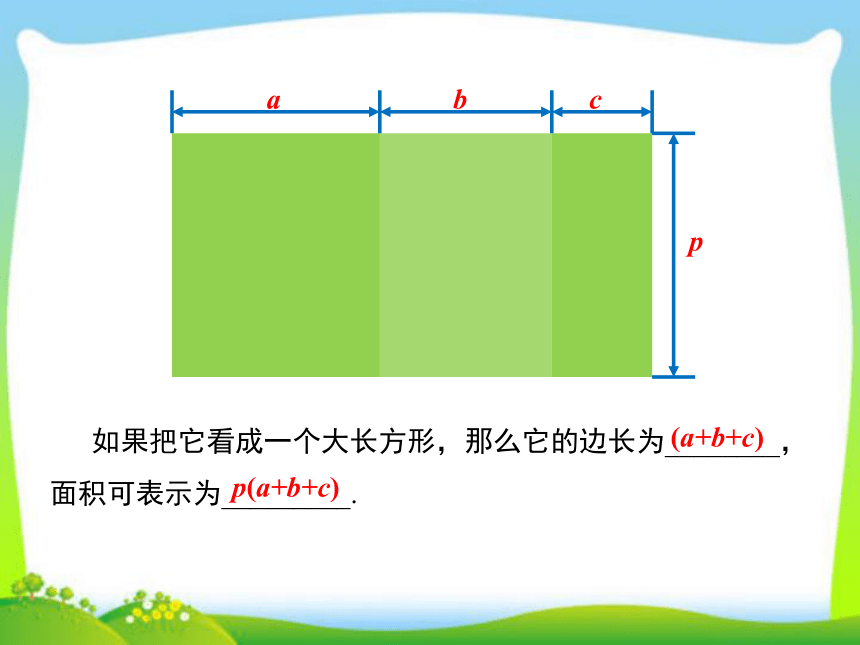
如果把它看成一个大长方形,那么它的边长为________,面积可表示为_________.
p(a+b+c)
(a+b+c)
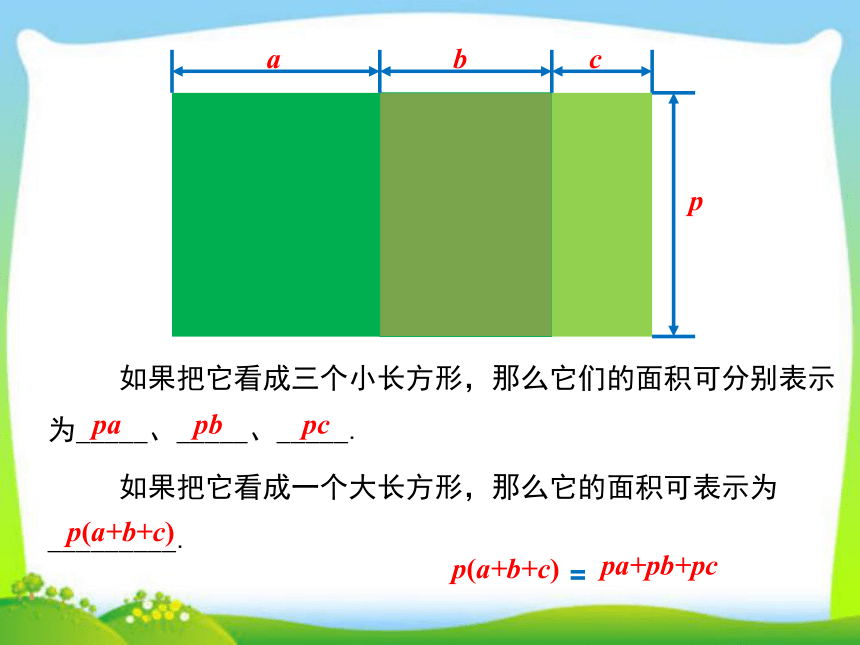
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
如果把它看成一个大长方形,那么它的面积可表示为_________.
pa
pc
pb
p(a+b+c)
pa+pb+pc
p(a+b+c)
c
b
a
p
=
p (a + b+ c)
pb
+
pc
pa
+
根据乘法的分配律
pa+pb+pc
p(a+b+c)
=
=
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再将所得的积相加.
用字母表示如下:
单项式与多项式的乘法法则
p(a+b+c)=pa+pb+pc
注意:(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
【例 】 计算:(-2a2)·(3ab2-5ab3).
解:(-2a2)·(3ab2-5ab3)
=(-2a2)·3ab2 +(-2a2)·(-5ab3)
=-6a3b2+10a3b3.
1.单项式与多项式相乘,就是用单项式去乘多项式的________,
再把所得的积________.
2.4(a-b+1)=________________.
每一项
相加
4a-4b+4
3.3x(2x-y2)=_________________.
6x2-3xy2
4.(2x-5y+6z)(-3x) =________________.
-6x2+15xy-18xz
5.(-2a2)2(-a-2b+c)=_________________.
-4a5-8a4b+4a4c
随堂即练
6.计算:-2x2·(xy+y2)-5x(x2y-xy2).
解:原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3 y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3 y+3x2y2.
7.先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),其中a=-2.
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
当a=-2时,原式=-20×(-2)2+9×(-2)=-98.
住宅用地
人民广场
商业用地
3a
3a+2b
2a-b
4a
8.如图,一块长方形地用来建造住宅、广场、商厦,
求这块地的面积.
解:4a[(3a+2b)+(2a-b)]
=4a(5a+b)
=4a·5a+4a·b
=20a2+4ab.
答:这块地的面积
为20a2+4ab.
单项式与多项式相乘
法则
转化为单项式乘单项式
注意
(1)计算时注意符号问题,单项式分别与多项式的每一项相乘时,同号得正,异号得负;
(2)不要出现漏乘现象;
(3)运算顺序:先乘方,再乘除,最后加减;
(4)对于混合运算最后应合并同类项
实质
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再把所得的积相加.
字母表示:p(a+b+c)=pa+pb+pc
课堂总结
第2课时 单项式与多项式相乘
九江一中 数学组
把它们看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
p
p
a
b
p
c
pa
pc
pb
单项式与多项式相乘
p
p
a
b
p
c
c
b
a
p
如果把它看成一个大长方形,那么它的边长为________,面积可表示为_________.
p(a+b+c)
(a+b+c)
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
如果把它看成一个大长方形,那么它的面积可表示为_________.
pa
pc
pb
p(a+b+c)
pa+pb+pc
p(a+b+c)
c
b
a
p
=
p (a + b+ c)
pb
+
pc
pa
+
根据乘法的分配律
pa+pb+pc
p(a+b+c)
=
=
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再将所得的积相加.
用字母表示如下:
单项式与多项式的乘法法则
p(a+b+c)=pa+pb+pc
注意:(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
【例 】 计算:(-2a2)·(3ab2-5ab3).
解:(-2a2)·(3ab2-5ab3)
=(-2a2)·3ab2 +(-2a2)·(-5ab3)
=-6a3b2+10a3b3.
1.单项式与多项式相乘,就是用单项式去乘多项式的________,
再把所得的积________.
2.4(a-b+1)=________________.
每一项
相加
4a-4b+4
3.3x(2x-y2)=_________________.
6x2-3xy2
4.(2x-5y+6z)(-3x) =________________.
-6x2+15xy-18xz
5.(-2a2)2(-a-2b+c)=_________________.
-4a5-8a4b+4a4c
随堂即练
6.计算:-2x2·(xy+y2)-5x(x2y-xy2).
解:原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3 y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3 y+3x2y2.
7.先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),其中a=-2.
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
当a=-2时,原式=-20×(-2)2+9×(-2)=-98.
住宅用地
人民广场
商业用地
3a
3a+2b
2a-b
4a
8.如图,一块长方形地用来建造住宅、广场、商厦,
求这块地的面积.
解:4a[(3a+2b)+(2a-b)]
=4a(5a+b)
=4a·5a+4a·b
=20a2+4ab.
答:这块地的面积
为20a2+4ab.
单项式与多项式相乘
法则
转化为单项式乘单项式
注意
(1)计算时注意符号问题,单项式分别与多项式的每一项相乘时,同号得正,异号得负;
(2)不要出现漏乘现象;
(3)运算顺序:先乘方,再乘除,最后加减;
(4)对于混合运算最后应合并同类项
实质
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再把所得的积相加.
字母表示:p(a+b+c)=pa+pb+pc
课堂总结
