沪教版(上海)数学八年级第二学期-22.3 特殊的平行四边形复习 课件(15张PPT)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.3 特殊的平行四边形复习 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 562.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:00:00 | ||
图片预览



文档简介
特殊的平行四边形复习
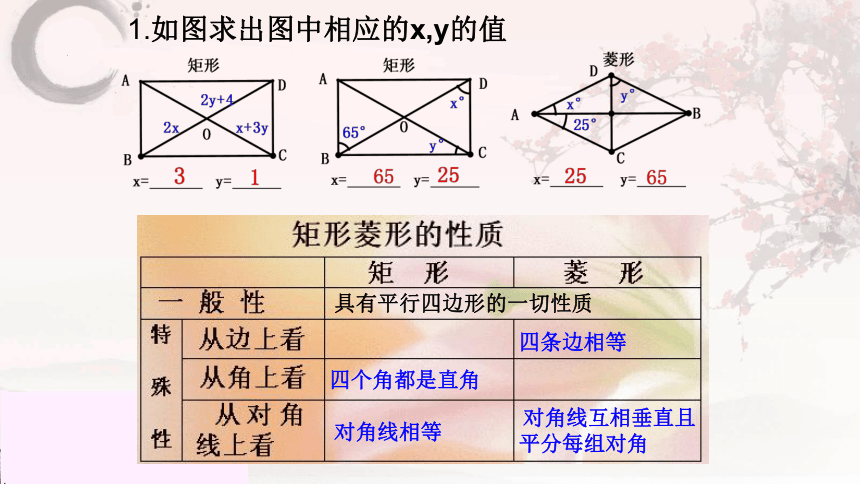
1.如图求出图中相应的x,y的值
具有平行四边形的一切性质
四个角都是直角
对角线相等
对角线互相垂直且平分每组对角
四条边相等
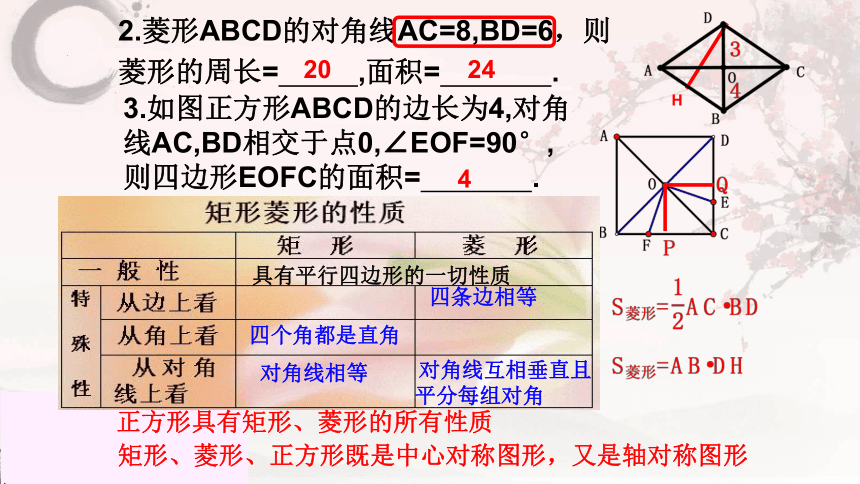
2.菱形ABCD的对角线AC=8,BD=6,则
菱形的周长= ,面积= .
3.如图正方形ABCD的边长为4,对角线AC,BD相交于点0,∠EOF=90°,
则四边形EOFC的面积= .
具有平行四边形的一切性质
四个角都是直角
对角线相等
对角线互相垂直且平分每组对角
四条边相等
20
24
H
正方形具有矩形、菱形的所有性质
4
矩形、菱形、正方形既是中心对称图形,又是轴对称图形
4.(1)下列菱形具有而矩形不一定具有的性质是( )
(2)下列矩形具有而菱形不一定具有的性质是( )
(A)对角线互相平分 (B)对角线相等
(C)对角线互相垂直 (D)对边平行且相等
C
B
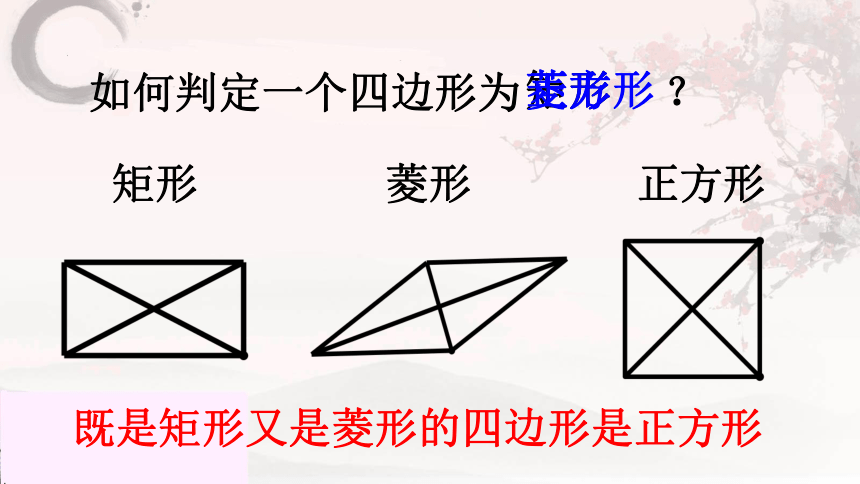
如何判定一个四边形为 ?
矩形
正方形
矩形
正方形
菱形
菱形
既是矩形又是菱形的四边形是正方形
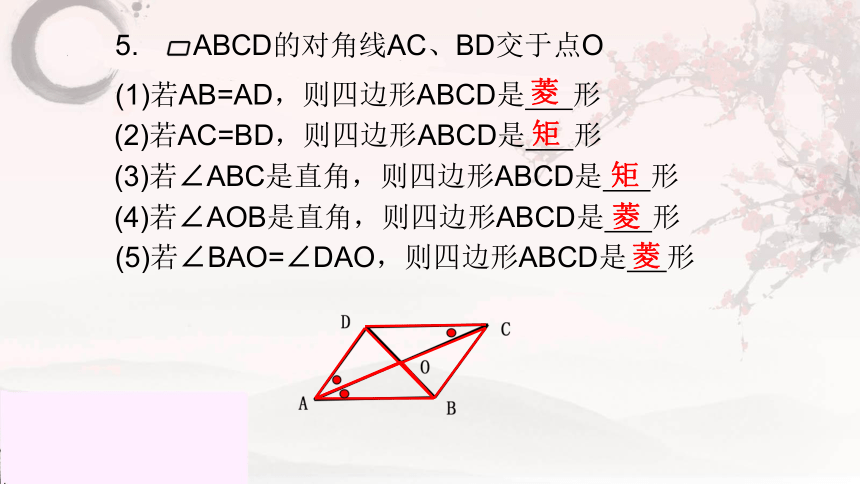
5. ABCD的对角线AC、BD交于点O
(1)若AB=AD,则四边形ABCD是 形
(2)若AC=BD,则四边形ABCD是 形
(3)若∠ABC是直角,则四边形ABCD是 形
(4)若∠AOB是直角,则四边形ABCD是 形
(5)若∠BAO=∠DAO,则四边形ABCD是 形
菱
矩
矩
菱
菱
6.填上适当的条件,使下列命题为真命题
(1)对角线 的四边形是矩形
(2)对角线 的平行四边形是矩形
(3)对角线 的四边形是菱形
(4)对角线 的平行四边形是菱形
互相平分且相等
相等
互相垂直平分
互相垂直
7.如图,矩形ABCD的对角线AC、BD相交于点O,OE∥AD交CD于点F, 且OF=FE,联结DE、CE.求证:四边形OCED是菱形.
证明:
∵四边形ABCD是矩形
∴∠ADC=90°
∴OD=OC
∵OE∥AD,∴∠OFC=∠ADC=90°,即OE⊥CD
即OD=OC,OE⊥CD可知DF=CF,又∵OF=FE
∴四边形OCED是平行四边形
∵OD=OC
∴四边形OCED是菱形
∵OE⊥DC
7.如图,矩形ABCD的对角线AC、BD相交于点O,OE∥AD交CD于点F, 且OF=FE,联结DE、CE.求证:四边形OCED是菱形.
证明:
∵四边形ABCD是矩形
∴∠ADC=90° AO=CO
∴∠OFC=∠ADC=90°,即OE⊥CD
∴四边形OCED是平行四边形
∵OE⊥DC
∴四边形OCED是菱形
∴DF=CF
∵OE∥AD
且AO=CO
又∵OF=FE
7.如图,矩形ABCD的对角线AC、BD相交于点O,OE∥AD交CD于点F, 且OF=FE,联结DE、CE.求证:四边形OCED是菱形.
证明:
∵四边形ABCD是矩形
∴∠ADC=90°
∵OE∥AD,∴∠OFC=∠ADC=90°,即CD⊥OE
又∵OF=FE ∴CD垂直平分OE
即DO=DE=CE=OC
∴四边形OCED是菱形
∴OD=DE,OC=CE
8.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,∠ACB与其邻补角∠ACD的角平分线分别交直线MN于点E,F,联结AE,AF.
(1)猜想:当点O为AC中点时,则四边形AECF是怎样的一个特殊的四边形,并且证明你的猜想.
8.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,∠ACB与其邻补角∠ACD的角平分线分别交直线MN于点E,F,联结AE,AF.
(1)猜想:当点O为AC中点时,则四边形AECF是怎样的一个特殊的四边形,并且证明你的猜想.
(2)当点O为AC中点时,如何改变△ABC的形状可使(1)中的四边形AECF为正方形.
解:四边形AECF是矩形
∵MN∥BC ∴∠1=∠2
∵∠2=∠3 ∴∠1=∠3
∴OC=OF
同理 OC=OE ∴OE=OF
∵AC=CO
∴四边形AECF是平行四边形
∵AO=CO=EO=FO,即可得AC=EF
∴四边形AECF是矩形
1
2
3
8.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,∠ACB与其邻补角∠ACD的角平分线分别交直线MN于点E,F,联结AE,AF.
45°
布置作业
如何判定一个四边形为 ?
矩形
正方形
菱形
2.菱形ABCD的对角线AC=8,BD=6,则
菱形的周长= ,面积= .
3.如图正方形ABCD的边长为4,对角线AC,BD相交于点0,∠EOF=90°,
则四边形EOFC的面积= .
具有平行四边形的一切性质
四个角都是直角
对角线相等
对角线互相垂直且平分每组对角
四条边相等
20
24
H
正方形具有矩形、菱形的所有性质
4
矩形、菱形、正方形既是中心对称图形,又是轴对称图形
1.如图求出图中相应的x,y的值
具有平行四边形的一切性质
四个角都是直角
对角线相等
对角线互相垂直且平分每组对角
四条边相等
2.菱形ABCD的对角线AC=8,BD=6,则
菱形的周长= ,面积= .
3.如图正方形ABCD的边长为4,对角线AC,BD相交于点0,∠EOF=90°,
则四边形EOFC的面积= .
具有平行四边形的一切性质
四个角都是直角
对角线相等
对角线互相垂直且平分每组对角
四条边相等
20
24
H
正方形具有矩形、菱形的所有性质
4
矩形、菱形、正方形既是中心对称图形,又是轴对称图形
4.(1)下列菱形具有而矩形不一定具有的性质是( )
(2)下列矩形具有而菱形不一定具有的性质是( )
(A)对角线互相平分 (B)对角线相等
(C)对角线互相垂直 (D)对边平行且相等
C
B
如何判定一个四边形为 ?
矩形
正方形
矩形
正方形
菱形
菱形
既是矩形又是菱形的四边形是正方形
5. ABCD的对角线AC、BD交于点O
(1)若AB=AD,则四边形ABCD是 形
(2)若AC=BD,则四边形ABCD是 形
(3)若∠ABC是直角,则四边形ABCD是 形
(4)若∠AOB是直角,则四边形ABCD是 形
(5)若∠BAO=∠DAO,则四边形ABCD是 形
菱
矩
矩
菱
菱
6.填上适当的条件,使下列命题为真命题
(1)对角线 的四边形是矩形
(2)对角线 的平行四边形是矩形
(3)对角线 的四边形是菱形
(4)对角线 的平行四边形是菱形
互相平分且相等
相等
互相垂直平分
互相垂直
7.如图,矩形ABCD的对角线AC、BD相交于点O,OE∥AD交CD于点F, 且OF=FE,联结DE、CE.求证:四边形OCED是菱形.
证明:
∵四边形ABCD是矩形
∴∠ADC=90°
∴OD=OC
∵OE∥AD,∴∠OFC=∠ADC=90°,即OE⊥CD
即OD=OC,OE⊥CD可知DF=CF,又∵OF=FE
∴四边形OCED是平行四边形
∵OD=OC
∴四边形OCED是菱形
∵OE⊥DC
7.如图,矩形ABCD的对角线AC、BD相交于点O,OE∥AD交CD于点F, 且OF=FE,联结DE、CE.求证:四边形OCED是菱形.
证明:
∵四边形ABCD是矩形
∴∠ADC=90° AO=CO
∴∠OFC=∠ADC=90°,即OE⊥CD
∴四边形OCED是平行四边形
∵OE⊥DC
∴四边形OCED是菱形
∴DF=CF
∵OE∥AD
且AO=CO
又∵OF=FE
7.如图,矩形ABCD的对角线AC、BD相交于点O,OE∥AD交CD于点F, 且OF=FE,联结DE、CE.求证:四边形OCED是菱形.
证明:
∵四边形ABCD是矩形
∴∠ADC=90°
∵OE∥AD,∴∠OFC=∠ADC=90°,即CD⊥OE
又∵OF=FE ∴CD垂直平分OE
即DO=DE=CE=OC
∴四边形OCED是菱形
∴OD=DE,OC=CE
8.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,∠ACB与其邻补角∠ACD的角平分线分别交直线MN于点E,F,联结AE,AF.
(1)猜想:当点O为AC中点时,则四边形AECF是怎样的一个特殊的四边形,并且证明你的猜想.
8.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,∠ACB与其邻补角∠ACD的角平分线分别交直线MN于点E,F,联结AE,AF.
(1)猜想:当点O为AC中点时,则四边形AECF是怎样的一个特殊的四边形,并且证明你的猜想.
(2)当点O为AC中点时,如何改变△ABC的形状可使(1)中的四边形AECF为正方形.
解:四边形AECF是矩形
∵MN∥BC ∴∠1=∠2
∵∠2=∠3 ∴∠1=∠3
∴OC=OF
同理 OC=OE ∴OE=OF
∵AC=CO
∴四边形AECF是平行四边形
∵AO=CO=EO=FO,即可得AC=EF
∴四边形AECF是矩形
1
2
3
8.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,∠ACB与其邻补角∠ACD的角平分线分别交直线MN于点E,F,联结AE,AF.
45°
布置作业
如何判定一个四边形为 ?
矩形
正方形
菱形
2.菱形ABCD的对角线AC=8,BD=6,则
菱形的周长= ,面积= .
3.如图正方形ABCD的边长为4,对角线AC,BD相交于点0,∠EOF=90°,
则四边形EOFC的面积= .
具有平行四边形的一切性质
四个角都是直角
对角线相等
对角线互相垂直且平分每组对角
四条边相等
20
24
H
正方形具有矩形、菱形的所有性质
4
矩形、菱形、正方形既是中心对称图形,又是轴对称图形
