沪教版(上海)数学八年级第二学期22.3.2菱形的性质 课件(18张PPT)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期22.3.2菱形的性质 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 365.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 23:00:24 | ||
图片预览


文档简介
22.3(2)菱形的性质
第二十二章 四边形
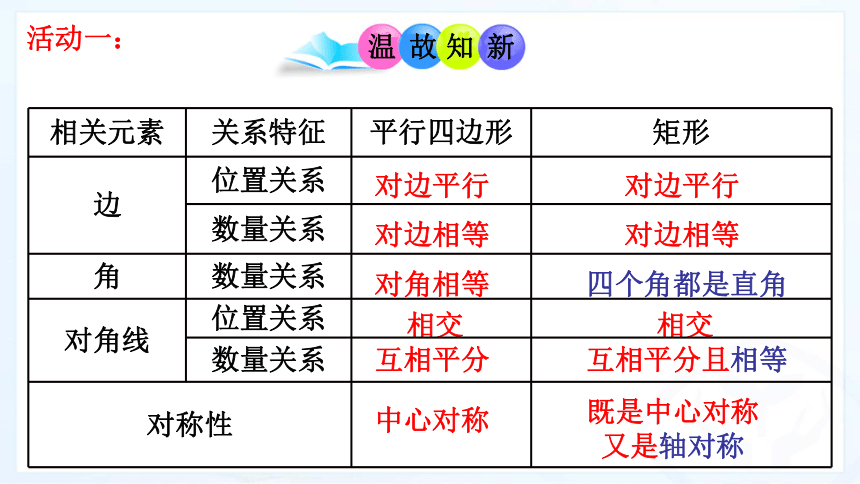
活动一:
对边平行
相交
互相平分
中心对称
对边相等
四个角都是直角
相交
互相平分且相等
既是中心对称
又是轴对称
温
故
知
新
对边平行
对边相等
对角相等
{5940675A-B579-460E-94D1-54222C63F5DA}相关元素
关系特征
平行四边形
矩形
边
位置关系
数量关系
角
数量关系
对角线
位置关系
数量关系
对称性
探
究
新
知
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
活动二:
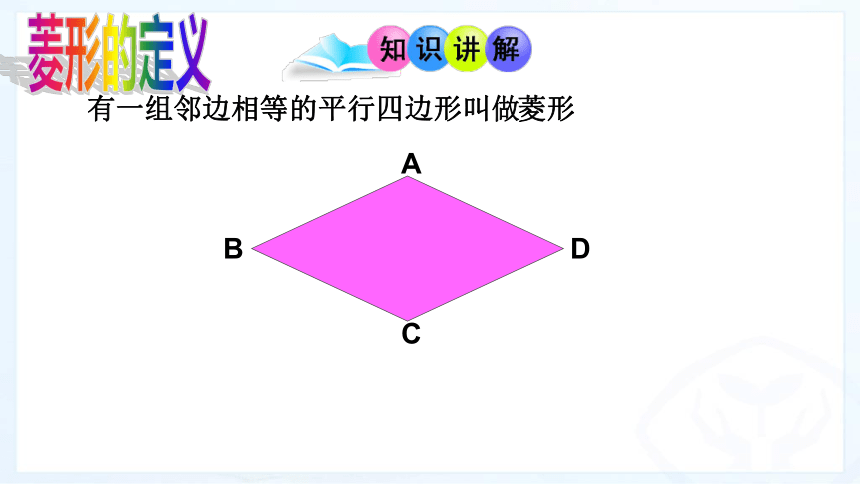
菱形的定义
邻边相等
平行四边形
菱形
有一组 的 叫做
D
A
C
B
探
究
新
知
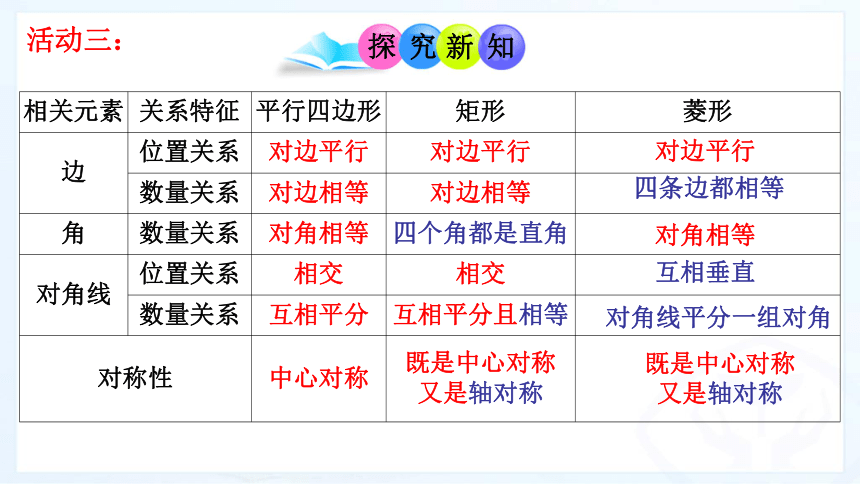
活动三:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}相关元素
关系特征
平行四边形
矩形
菱形
边
位置关系
对边平行
对边平行
数量关系
对边相等
对边相等
角
数量关系
对角相等
四个角都是直角
对角线
位置关系
相交
相交
数量关系
互相平分
互相平分且相等
对称性
中心对称
既是中心对称
又是轴对称
对边平行
四条边都相等
对角相等
互相垂直
对角线平分一组对角
既是中心对称 又是轴对称
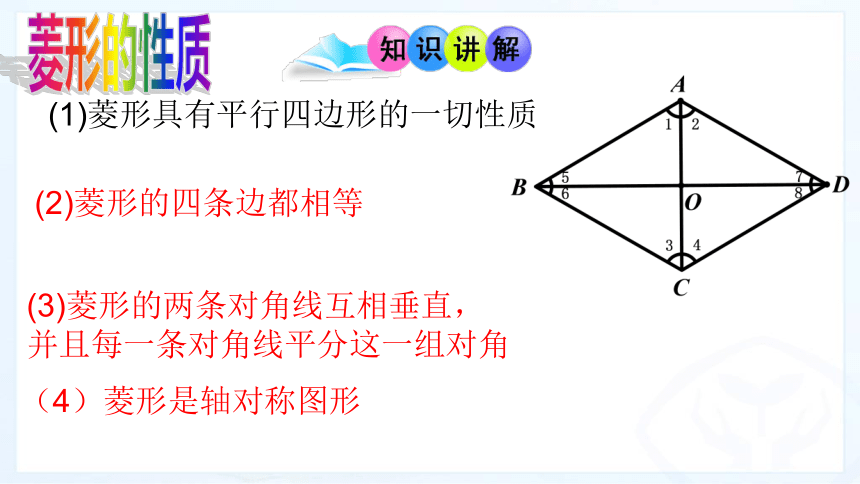
菱形的性质
(1)菱形具有平行四边形的一切性质
(2)菱形的四条边都相等
(3)菱形的两条对角线互相垂直,
并且每一条对角线平分这一组对角
(4)菱形是轴对称图形
知
识
讲
解
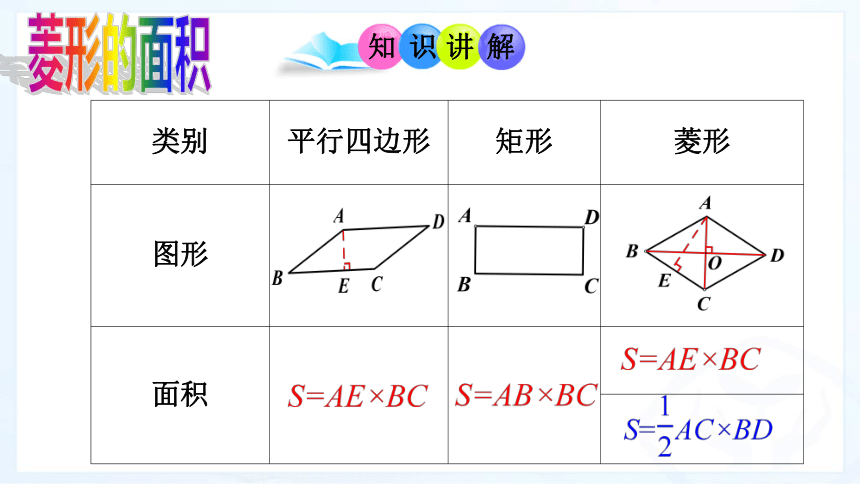
菱形的面积
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}类别
平行四边形
矩形
菱形
图形
面积
活动四:
1.菱形具有而平行四边形不一定具有的性质是( )
A.对角相等 B.对边平行
C.对角线互相平分 D.对角线互相垂直
D
活动四:
2、菱形ABCD的面积为24cm2,其中对角线AC长是6cm,
则菱形的边长 ,周长 。
5cm
20cm
活动四:
3、已知菱形ABCD,AB=4cm,∠ABC=60°,
则菱形ABCD的面积为_________。
菱形ABCD的对角线AC与BD相交于点O,已知AB=13cm,AC=24cm,求这个菱形的面积
已知在菱形ABCD中,对角线BD,AC交于点O,AE⊥CD,AE交OD于点F,且AE=OD
求证:
F
E
如图,菱形ABCD中,∠B=60°,点E、F分别在边BC、CD上,且∠EAF=60°.
试探究AE与AF之间存在怎
样的数量关系?并说明理由.
1
2
3
如图,菱形ABCD中,∠B=60°,点E、F分别在边BC、CD上,且∠EAF=60°.
试探究AE与AF之间存在怎
样的数量关系?并说明理由.
1
2
3
活动五:
例题变式训练1:如图,菱形ABCD中,∠ABC=60°,点E、F分别在边CB、DC延长线上,且∠EAF=60°.问AE=AF是否仍然成立?若成立,请说明理由.
变
式
训
练
提示:联结AC
1
2
3
2
证明△ABE △ACF
拓
展
提
高
例题变式训练2:如图,菱形ABCD中,∠B=60°,点E、F分别在边CB、DC边上,且∠AEF=60°.问AE=AF是否仍然成立?若成立,请说明理由.
证明△AEM △EFC(ASA)
≌
提示:联结AC,过点E作 EM//AC交AB于M点
(或在AB上截取AM使AM=CE)
1
2
活动六:
畅
所
欲
言
对自己说我有哪些收获?
对同学有哪些温馨提示?
对老师说你还有哪些困惑?
作
业
布
置
必做作业:练习册22.3(2)
选做作业:思考题
给你一张任意形状的三角形纸片,你能以三角形纸片的其中
一个内角为菱形的一个内角,折出一个菱形吗?
第二十二章 四边形
活动一:
对边平行
相交
互相平分
中心对称
对边相等
四个角都是直角
相交
互相平分且相等
既是中心对称
又是轴对称
温
故
知
新
对边平行
对边相等
对角相等
{5940675A-B579-460E-94D1-54222C63F5DA}相关元素
关系特征
平行四边形
矩形
边
位置关系
数量关系
角
数量关系
对角线
位置关系
数量关系
对称性
探
究
新
知
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
活动二:
菱形的定义
邻边相等
平行四边形
菱形
有一组 的 叫做
D
A
C
B
探
究
新
知
活动三:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}相关元素
关系特征
平行四边形
矩形
菱形
边
位置关系
对边平行
对边平行
数量关系
对边相等
对边相等
角
数量关系
对角相等
四个角都是直角
对角线
位置关系
相交
相交
数量关系
互相平分
互相平分且相等
对称性
中心对称
既是中心对称
又是轴对称
对边平行
四条边都相等
对角相等
互相垂直
对角线平分一组对角
既是中心对称 又是轴对称
菱形的性质
(1)菱形具有平行四边形的一切性质
(2)菱形的四条边都相等
(3)菱形的两条对角线互相垂直,
并且每一条对角线平分这一组对角
(4)菱形是轴对称图形
知
识
讲
解
菱形的面积
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}类别
平行四边形
矩形
菱形
图形
面积
活动四:
1.菱形具有而平行四边形不一定具有的性质是( )
A.对角相等 B.对边平行
C.对角线互相平分 D.对角线互相垂直
D
活动四:
2、菱形ABCD的面积为24cm2,其中对角线AC长是6cm,
则菱形的边长 ,周长 。
5cm
20cm
活动四:
3、已知菱形ABCD,AB=4cm,∠ABC=60°,
则菱形ABCD的面积为_________。
菱形ABCD的对角线AC与BD相交于点O,已知AB=13cm,AC=24cm,求这个菱形的面积
已知在菱形ABCD中,对角线BD,AC交于点O,AE⊥CD,AE交OD于点F,且AE=OD
求证:
F
E
如图,菱形ABCD中,∠B=60°,点E、F分别在边BC、CD上,且∠EAF=60°.
试探究AE与AF之间存在怎
样的数量关系?并说明理由.
1
2
3
如图,菱形ABCD中,∠B=60°,点E、F分别在边BC、CD上,且∠EAF=60°.
试探究AE与AF之间存在怎
样的数量关系?并说明理由.
1
2
3
活动五:
例题变式训练1:如图,菱形ABCD中,∠ABC=60°,点E、F分别在边CB、DC延长线上,且∠EAF=60°.问AE=AF是否仍然成立?若成立,请说明理由.
变
式
训
练
提示:联结AC
1
2
3
2
证明△ABE △ACF
拓
展
提
高
例题变式训练2:如图,菱形ABCD中,∠B=60°,点E、F分别在边CB、DC边上,且∠AEF=60°.问AE=AF是否仍然成立?若成立,请说明理由.
证明△AEM △EFC(ASA)
≌
提示:联结AC,过点E作 EM//AC交AB于M点
(或在AB上截取AM使AM=CE)
1
2
活动六:
畅
所
欲
言
对自己说我有哪些收获?
对同学有哪些温馨提示?
对老师说你还有哪些困惑?
作
业
布
置
必做作业:练习册22.3(2)
选做作业:思考题
给你一张任意形状的三角形纸片,你能以三角形纸片的其中
一个内角为菱形的一个内角,折出一个菱形吗?
