沪教版(上海)数学九年级第二学期-27.3 垂径定理 课件(16张PPT)
文档属性
| 名称 | 沪教版(上海)数学九年级第二学期-27.3 垂径定理 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 230.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:00:00 | ||
图片预览




文档简介
27.3垂径定理
驶向胜利的彼岸
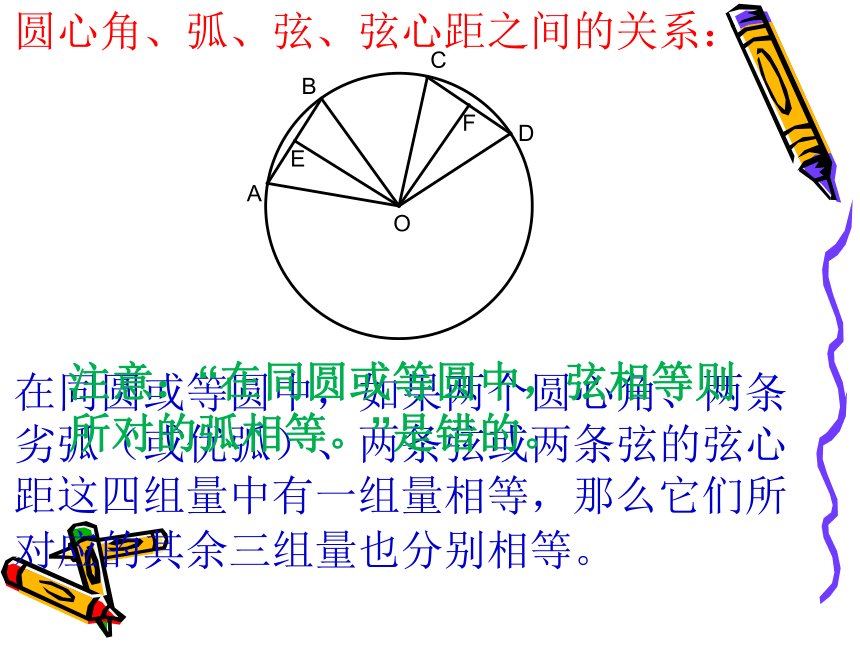
圆心角、弧、弦、弦心距之间的关系:
在同圆或等圆中,如果两个圆心角、两条劣弧(或优弧)、两条弦或两条弦的弦心距这四组量中有一组量相等,那么它们所对应的其余三组量也分别相等。
注意:“在同圆或等圆中,弦相等则所对的弧相等。”是错的。
对称轴是 。
任意一条直径所在的直线
圆是 对称图形,
也是中心对称图形,
圆还是 对称图形,
轴
旋转
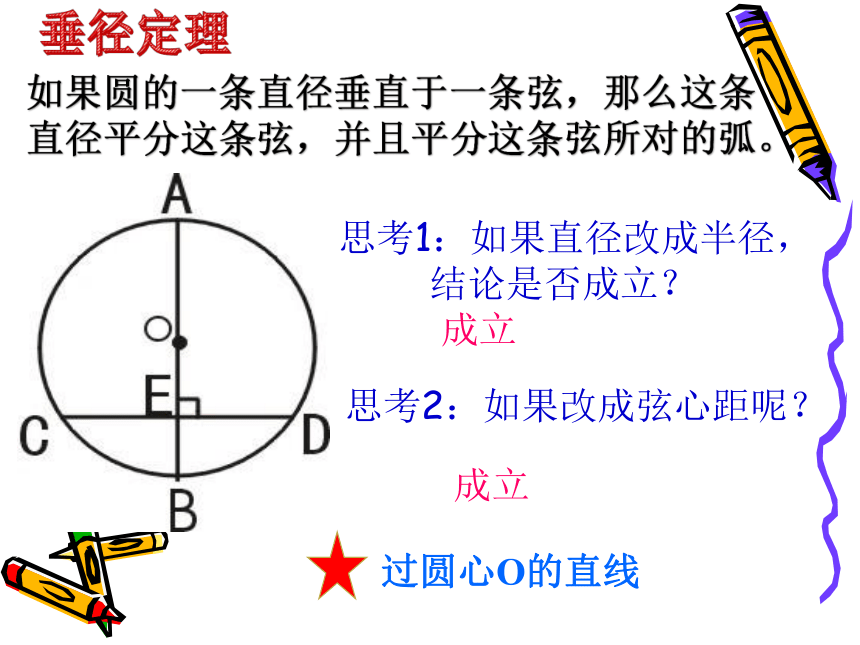
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧。
思考1:如果直径改成半径,
结论是否成立?
成立
成立
垂径定理
过圆心O的直线
思考2:如果改成弦心距呢?
观察图形,说出图中的弦CD是否被AB平分,
为什么?
小结:垂径定理成立的两个要点是什么?
图中的AB必须经过圆心,
AB必须垂直于 CD 。
A
B
C
D
M
O
A
B
C
D
M
O
A
B
C
D
M
O
(1)
(2)
(3)
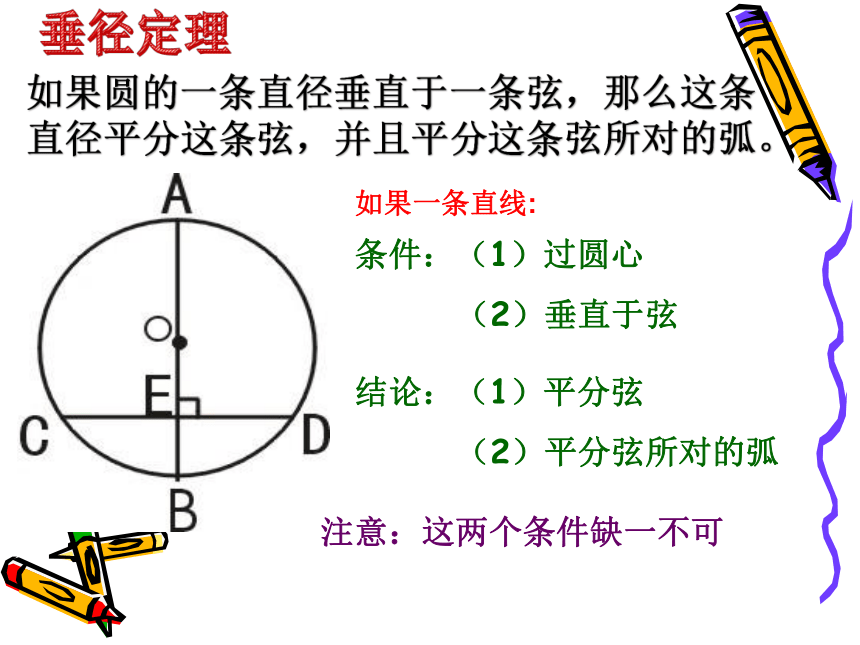
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧。
垂径定理
条件:(1)过圆心
(2)垂直于弦
结论:(1)平分弦
(2)平分弦所对的弧
注意:这两个条件缺一不可
如果一条直线:
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧。
垂径定理
判断:(1)垂直于弦的直线平分弦。
(2)圆的半径垂直于弦时,必平分这 条弦及弦所对的弧。
例1:
如图:半径OC垂直于弦AB,垂足为D,
(1)BC长6cm,求AC的长;
(2) 圆O的半径为5cm,AB=8cm,求OD的长。
A
B
C
D
O
︵
︵
2
6
练习:
1、 如图半径OC垂直于弦AB,垂足为点D
AB=4cm , BC=3cm ,
那么AD=_____cm ,
AB=_____cm
︵
︵
2、OC是弦AB的弦心距,
若AC=8cm, 则AB=______cm
O
C
A
B
16
例2:
已知以点O为圆心的两个圆中,大
圆的弦AB交小圆于C,D两个点,
那么AC=BD吗?
为什么?
例3:已知如图:OD是 ⊙O的半径,AB是弦,OD⊥AB,
△ADB是什么三角形?为什么?
解:∵ OD是 ⊙O的半径 ,
且OD⊥AB (已知)
∴ AD=BD
(同圆中如果弧相等,那么所对
的弦相等)
O
D
A
B
∴ △ADB是等腰三角形
∴AD=BD
(
)
︵
︵
思考:
若连接OA与OB,则∠AOD与∠BOD相等吗?
如果圆的一条直径垂直于一条弦,
那么这条直径平分弦所对的弧
问题 :你知道赵州桥吗?它是1400多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
赵州桥主桥拱的半径是多少?
拓展练习1:
如图,P为圆O内一点,
利用三角尺画一条弦AB,使AB过点P,并且AP=BP
O
P
A
B
如图:已知在圆O中,弦AB和弦CD是两条
互相平行的弦,AC与BD相等吗?
为什么?
O
A
B
C
D
E
F
拓展练习2:
课堂小结:
1.圆是轴对称图形,直径所在的直线是它的对称轴.
2.垂直于弦的直径的性质:如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧。
强调两个条件:①过圆心 ②垂直于弦
这两个条件缺一不可。
驶向胜利的彼岸
圆心角、弧、弦、弦心距之间的关系:
在同圆或等圆中,如果两个圆心角、两条劣弧(或优弧)、两条弦或两条弦的弦心距这四组量中有一组量相等,那么它们所对应的其余三组量也分别相等。
注意:“在同圆或等圆中,弦相等则所对的弧相等。”是错的。
对称轴是 。
任意一条直径所在的直线
圆是 对称图形,
也是中心对称图形,
圆还是 对称图形,
轴
旋转
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧。
思考1:如果直径改成半径,
结论是否成立?
成立
成立
垂径定理
过圆心O的直线
思考2:如果改成弦心距呢?
观察图形,说出图中的弦CD是否被AB平分,
为什么?
小结:垂径定理成立的两个要点是什么?
图中的AB必须经过圆心,
AB必须垂直于 CD 。
A
B
C
D
M
O
A
B
C
D
M
O
A
B
C
D
M
O
(1)
(2)
(3)
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧。
垂径定理
条件:(1)过圆心
(2)垂直于弦
结论:(1)平分弦
(2)平分弦所对的弧
注意:这两个条件缺一不可
如果一条直线:
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧。
垂径定理
判断:(1)垂直于弦的直线平分弦。
(2)圆的半径垂直于弦时,必平分这 条弦及弦所对的弧。
例1:
如图:半径OC垂直于弦AB,垂足为D,
(1)BC长6cm,求AC的长;
(2) 圆O的半径为5cm,AB=8cm,求OD的长。
A
B
C
D
O
︵
︵
2
6
练习:
1、 如图半径OC垂直于弦AB,垂足为点D
AB=4cm , BC=3cm ,
那么AD=_____cm ,
AB=_____cm
︵
︵
2、OC是弦AB的弦心距,
若AC=8cm, 则AB=______cm
O
C
A
B
16
例2:
已知以点O为圆心的两个圆中,大
圆的弦AB交小圆于C,D两个点,
那么AC=BD吗?
为什么?
例3:已知如图:OD是 ⊙O的半径,AB是弦,OD⊥AB,
△ADB是什么三角形?为什么?
解:∵ OD是 ⊙O的半径 ,
且OD⊥AB (已知)
∴ AD=BD
(同圆中如果弧相等,那么所对
的弦相等)
O
D
A
B
∴ △ADB是等腰三角形
∴AD=BD
(
)
︵
︵
思考:
若连接OA与OB,则∠AOD与∠BOD相等吗?
如果圆的一条直径垂直于一条弦,
那么这条直径平分弦所对的弧
问题 :你知道赵州桥吗?它是1400多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
赵州桥主桥拱的半径是多少?
拓展练习1:
如图,P为圆O内一点,
利用三角尺画一条弦AB,使AB过点P,并且AP=BP
O
P
A
B
如图:已知在圆O中,弦AB和弦CD是两条
互相平行的弦,AC与BD相等吗?
为什么?
O
A
B
C
D
E
F
拓展练习2:
课堂小结:
1.圆是轴对称图形,直径所在的直线是它的对称轴.
2.垂直于弦的直径的性质:如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧。
强调两个条件:①过圆心 ②垂直于弦
这两个条件缺一不可。
