沪教版(上海)数学九年级第二学期-27.3 垂径定理(1) 课件(17张PPT)
文档属性
| 名称 | 沪教版(上海)数学九年级第二学期-27.3 垂径定理(1) 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 419.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:00:00 | ||
图片预览




文档简介
27.3 垂径定理(1)
问题情境
赵州桥的桥拱是圆弧形
你们知道它的半径吗?
实践探究
把一个圆沿着它的任意一条直径对折,你发现了什么?由此你能得到什么结论?
可以发现:
圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
活动一
实践探究
·
O
A
B
C
D
M
活动二
请同学们在自己手中的圆中作图:
图中有哪些相等的量?
可以得到:
AM=BM,AD= BD,AC=BC
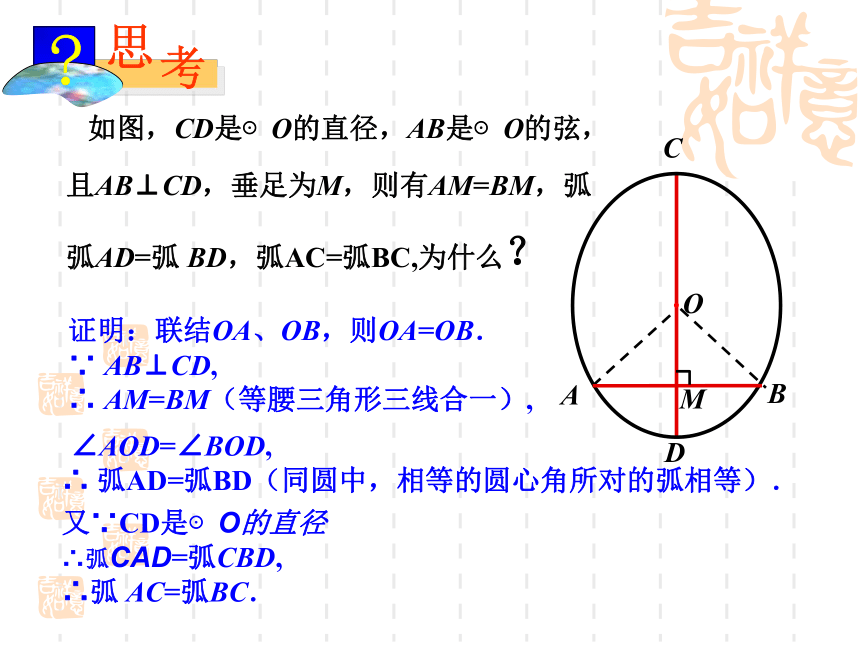
如图,CD是⊙O的直径,AB是⊙O的弦,且AB⊥CD,垂足为M,则有AM=BM,弧弧AD=弧 BD,弧AC=弧BC,为什么?
?
思
考
证明:联结OA、OB,则OA=OB.
∵ AB⊥CD,
∴ AM=BM(等腰三角形三线合一),
∠AOD=∠BOD,
∴ 弧AD=弧BD(同圆中,相等的圆心角所对的弧相等).
又∵CD是⊙O的直径
∴弧CAD=弧CBD,
∴弧 AC=弧BC.
·
O
A
B
C
D
M
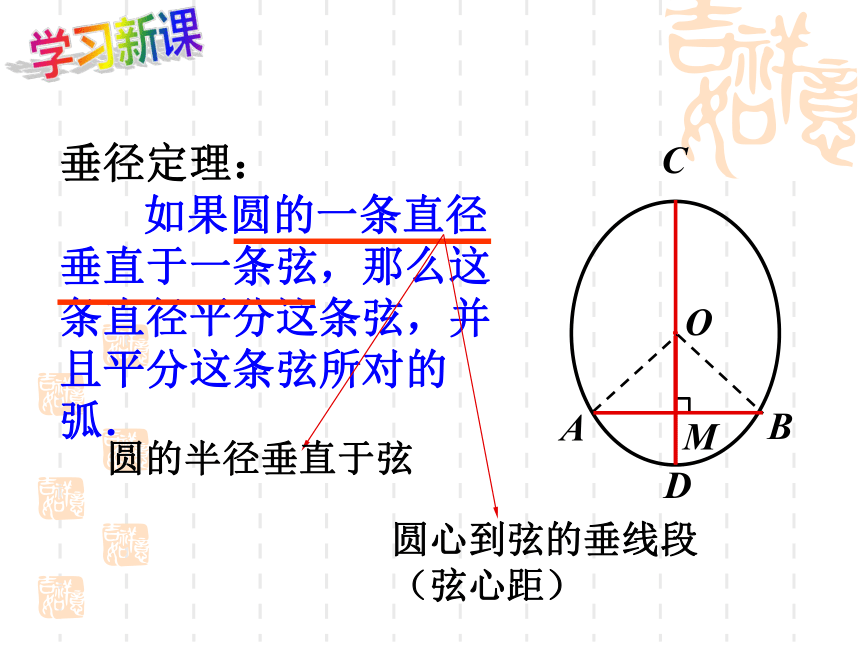
垂径定理:
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧.
·
O
A
B
C
D
M
圆的半径垂直于弦
圆心到弦的垂线段(弦心距)
学习新课
垂径定理:
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分弦所对的弧.
·
O
C
D
M
A
B
圆的半径垂直于弦
圆心到弦的垂线段(弦心距)
学习新课
这条弦可以是直径
A
B
例题1 已知:如图,以点O为圆心的两个圆中,大圆的弦AB交小圆于点C、D两点,
求证:AC=DB
o
A
C
B
D
H
学习新课
证明:过点O作OH⊥AB,垂足为点H.由垂径定理,得
CH=DH,AH=BH,
即AC+CH=BD+DH
∴AC=DB
A
C
F
B
D
E
O
如图,AB为⊙O的直径,CD是弦,EC⊥CD,FD⊥CD,点E、F在AB上.求证:AE=BF.
试一试
H
问题解决
例2(赵州桥桥拱问题)1300多年前,我国隋代建造的赵州石拱桥的桥拱是圆弧形,已知桥拱的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,求桥拱所在圆的半径长(精确到0.1米).
B
A
O
C
D
1.如图,已知⊙O的半径OC垂直于弦AB,垂足为点D,
(1)若AB=4,OD=3,则⊙O的半径OC=_____.
(2)若AB=8,OC=5,则 CD=_____.
试一试
(3)若OC=4,CD=2,则 AB=_____, ∠OAB=_____.
2
300
中考链接
金山区模拟考试第22题
A
O
H
B
C
(第22题图)
如图是公园中的一个圆弧形拱门,其中拱门的圆心是点O,拱门的最高处点A到地面的距离AH=3米,拱门的地面宽BC=2米,求拱门的半径。
自主小结
通过本节课的学习,谈谈你的收获---
练习册
布置作业
习题27.3(1)
拓展
已知圆的直径为10cm,在圆中有两条平行弦,长分别为8cm和6cm,求这两条平行弦之间的距离。
在⊙O中,直径AB和弦CD相交于点P,且∠APC=300.如果AP=2,PB=6,求CD的长.
拓展
谢谢!
问题情境
赵州桥的桥拱是圆弧形
你们知道它的半径吗?
实践探究
把一个圆沿着它的任意一条直径对折,你发现了什么?由此你能得到什么结论?
可以发现:
圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
活动一
实践探究
·
O
A
B
C
D
M
活动二
请同学们在自己手中的圆中作图:
图中有哪些相等的量?
可以得到:
AM=BM,AD= BD,AC=BC
如图,CD是⊙O的直径,AB是⊙O的弦,且AB⊥CD,垂足为M,则有AM=BM,弧弧AD=弧 BD,弧AC=弧BC,为什么?
?
思
考
证明:联结OA、OB,则OA=OB.
∵ AB⊥CD,
∴ AM=BM(等腰三角形三线合一),
∠AOD=∠BOD,
∴ 弧AD=弧BD(同圆中,相等的圆心角所对的弧相等).
又∵CD是⊙O的直径
∴弧CAD=弧CBD,
∴弧 AC=弧BC.
·
O
A
B
C
D
M
垂径定理:
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧.
·
O
A
B
C
D
M
圆的半径垂直于弦
圆心到弦的垂线段(弦心距)
学习新课
垂径定理:
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分弦所对的弧.
·
O
C
D
M
A
B
圆的半径垂直于弦
圆心到弦的垂线段(弦心距)
学习新课
这条弦可以是直径
A
B
例题1 已知:如图,以点O为圆心的两个圆中,大圆的弦AB交小圆于点C、D两点,
求证:AC=DB
o
A
C
B
D
H
学习新课
证明:过点O作OH⊥AB,垂足为点H.由垂径定理,得
CH=DH,AH=BH,
即AC+CH=BD+DH
∴AC=DB
A
C
F
B
D
E
O
如图,AB为⊙O的直径,CD是弦,EC⊥CD,FD⊥CD,点E、F在AB上.求证:AE=BF.
试一试
H
问题解决
例2(赵州桥桥拱问题)1300多年前,我国隋代建造的赵州石拱桥的桥拱是圆弧形,已知桥拱的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,求桥拱所在圆的半径长(精确到0.1米).
B
A
O
C
D
1.如图,已知⊙O的半径OC垂直于弦AB,垂足为点D,
(1)若AB=4,OD=3,则⊙O的半径OC=_____.
(2)若AB=8,OC=5,则 CD=_____.
试一试
(3)若OC=4,CD=2,则 AB=_____, ∠OAB=_____.
2
300
中考链接
金山区模拟考试第22题
A
O
H
B
C
(第22题图)
如图是公园中的一个圆弧形拱门,其中拱门的圆心是点O,拱门的最高处点A到地面的距离AH=3米,拱门的地面宽BC=2米,求拱门的半径。
自主小结
通过本节课的学习,谈谈你的收获---
练习册
布置作业
习题27.3(1)
拓展
已知圆的直径为10cm,在圆中有两条平行弦,长分别为8cm和6cm,求这两条平行弦之间的距离。
在⊙O中,直径AB和弦CD相交于点P,且∠APC=300.如果AP=2,PB=6,求CD的长.
拓展
谢谢!
