沪教版(上海)数学九年级第二学期27.6.1正多边形与圆 课件(18张PPT)
文档属性
| 名称 | 沪教版(上海)数学九年级第二学期27.6.1正多边形与圆 课件(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 597.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 23:04:30 | ||
图片预览




文档简介
27.6(1)
正多边形与圆
1.n边形的内角和等于_________,
n边形的外角和等于_________.
2.若六边形的每个内角都相等,则每个内角等于____________
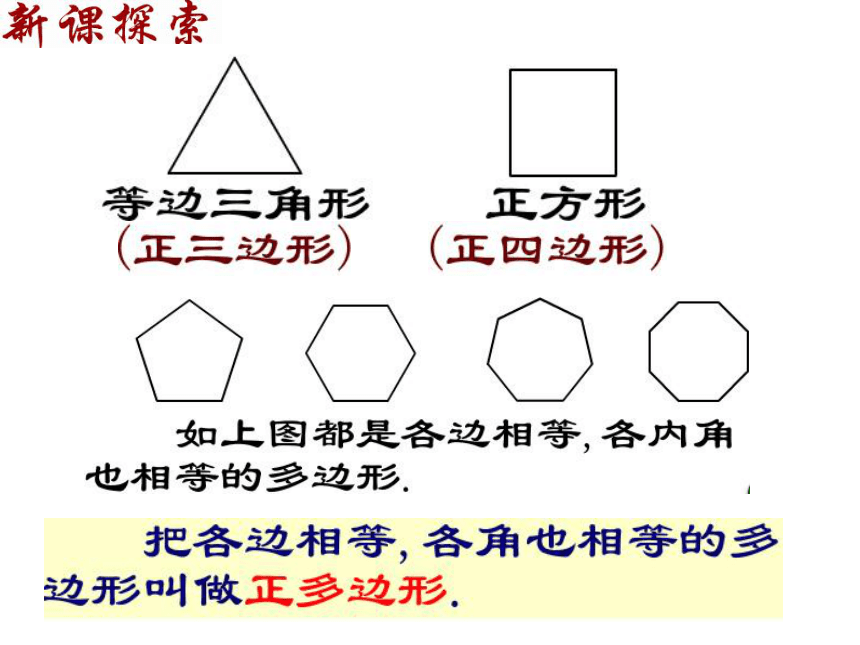
边数为五的正多边形叫做正五边形,边数为六的正多边形叫做正六边形.边数为n的正多边形(n是正整数且n≥3)就叫做正n边形.
想一想:
菱形是正多边形吗?矩形是正多边形吗?为什么?
菱形不一定是正多边形,因为各边相等,但各角不一定相等.
矩形不一定是正多边形,因为各角相等,但各边不一定相等.
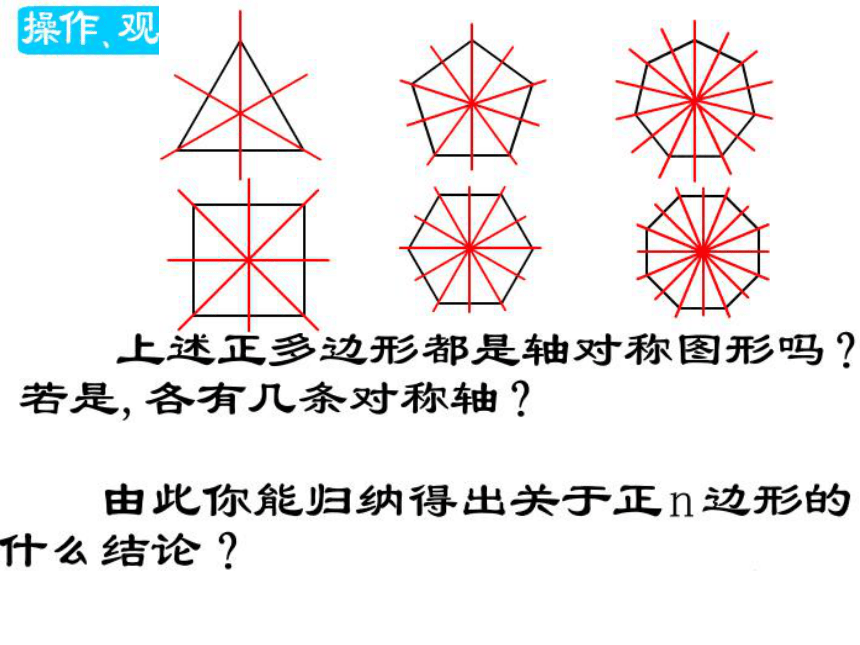
当n为奇数时,对称轴是各边的垂直平分线;
当n为偶数时,对称轴是一边的垂直平分线或过相对两内角的顶点的直线.
当n为奇数时,正n边形不是中心对称图形;
当n为偶数时,正n边形是中心对称图形,对称中心是两条对称轴的交点.
正n边形的n条对称轴交于一点。由正n边形是轴对称图形及其n条对称轴的位置特征,可知这个交点到正n边形________的距离相等,到正n边形________的距离也相等。
各顶点
各边
任何一个正多边形都有一个外接圆和一个内切圆(在一个多边形的内部且与多边形各边相切的圆叫做这个多边形的内切圆),外接圆和内切圆的圆心都是这个正多边形的对称轴的交点.
正多边形的外接圆(或内切圆)的圆心叫做正多边形的中心.
正多边形的外接圆的半径叫做正多边形的半径.
正多边形的内接圆的半径长叫做正多边形的边心距.
正多边形各边所对的外接圆的圆心角都相等.
正多边形一边所对的外接圆的圆心角叫做正多边形的中心角.
2.求证:在正n边形中,
1.中心角等于
2.中心角与每个内角互补.
1.正三角形的中心角等于_______,正方形的中心角等于_______,正六边形的中心角等于_______.
正n边形是旋转对称图形,旋转角大小是 .
它们具有怎样的旋转对称性?
120°240°
90°180°270°
60°120°180°
240°300°
例题:已知正n边形的一个中心角与一个内角之比为1:3,求n的值.
新知运用
拓展练习
A
B
C
D
E
F
G
H
I
如图,正三角形ABC的边长为6cm,正六边形DEFGHI的顶点分别在三角形三边上,求:这个正六边形的周长和面积.
1.正多边形的定义
2.正多边形的轴对称性
3.正多边形的中心对称性
4.正多边形的相关概念
5.正多边形的旋转对称性
正多边形与圆
1.n边形的内角和等于_________,
n边形的外角和等于_________.
2.若六边形的每个内角都相等,则每个内角等于____________
边数为五的正多边形叫做正五边形,边数为六的正多边形叫做正六边形.边数为n的正多边形(n是正整数且n≥3)就叫做正n边形.
想一想:
菱形是正多边形吗?矩形是正多边形吗?为什么?
菱形不一定是正多边形,因为各边相等,但各角不一定相等.
矩形不一定是正多边形,因为各角相等,但各边不一定相等.
当n为奇数时,对称轴是各边的垂直平分线;
当n为偶数时,对称轴是一边的垂直平分线或过相对两内角的顶点的直线.
当n为奇数时,正n边形不是中心对称图形;
当n为偶数时,正n边形是中心对称图形,对称中心是两条对称轴的交点.
正n边形的n条对称轴交于一点。由正n边形是轴对称图形及其n条对称轴的位置特征,可知这个交点到正n边形________的距离相等,到正n边形________的距离也相等。
各顶点
各边
任何一个正多边形都有一个外接圆和一个内切圆(在一个多边形的内部且与多边形各边相切的圆叫做这个多边形的内切圆),外接圆和内切圆的圆心都是这个正多边形的对称轴的交点.
正多边形的外接圆(或内切圆)的圆心叫做正多边形的中心.
正多边形的外接圆的半径叫做正多边形的半径.
正多边形的内接圆的半径长叫做正多边形的边心距.
正多边形各边所对的外接圆的圆心角都相等.
正多边形一边所对的外接圆的圆心角叫做正多边形的中心角.
2.求证:在正n边形中,
1.中心角等于
2.中心角与每个内角互补.
1.正三角形的中心角等于_______,正方形的中心角等于_______,正六边形的中心角等于_______.
正n边形是旋转对称图形,旋转角大小是 .
它们具有怎样的旋转对称性?
120°240°
90°180°270°
60°120°180°
240°300°
例题:已知正n边形的一个中心角与一个内角之比为1:3,求n的值.
新知运用
拓展练习
A
B
C
D
E
F
G
H
I
如图,正三角形ABC的边长为6cm,正六边形DEFGHI的顶点分别在三角形三边上,求:这个正六边形的周长和面积.
1.正多边形的定义
2.正多边形的轴对称性
3.正多边形的中心对称性
4.正多边形的相关概念
5.正多边形的旋转对称性
