沪教版(上海)初中数学八年级第一学期 19.9 勾股定理及其应用(一) 教案
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.9 勾股定理及其应用(一) 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 62.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览

文档简介
勾股定理及其应用(一)
教学目标
知识与技能
1、掌握勾股定理的内容.2、会初步运用勾股定理进行简单的计算、证明.
过程与方法
3、在探索勾股定理的过程中,让学生经历“操作—观察—猜想—归纳—验证”的数学思想,体会数形结合和特殊到一般的思想方法.
情感、态度与价值观
4、通过实验操作、探索,培养学生的学习兴趣、体验学习的乐趣.5、通过了解有关勾股定理的历史,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生奋发学习.
重点
勾股定理的掌握及其应用
难点
用面积割补法证明勾股定理
教师活动
学生活动
设计意图
创设情境提出问题
老师小时侯有过这么一个疑问:如图:从A点位置向西走3步到C点,再从C点位置向北走4步到B点位置,问从A点到B点需要走几步?若A点到C点改为6步,C点到B改为7步,则从A点到B点需要走几步?
第一个问题:5步(多数学生)第二个问题:8步(有学生这样回答,会有争议)
激发学生好奇心和求知欲,使学生带着疑问进行学习,增强学习的兴趣,同时了解生活中的数学,从生活中的实际问题导入,使学生体会数学来源于生.
探索发现猜想归纳
要求学生拿出准备好的硬纸片和剪刀,四组同学一分为二,两组画直角边为3cm和4
cm的直角三角形,两组画直角边为6cm和7cm的直角三角形,并剪下三角形,量取斜边的长度.要求学生找找3、4、5这三个数有何特殊关系?而6、7、8这3个数是无此关系的.(教师引导)直角边为6cm和7cm的直角三角形斜边长为多少呢?是否所有的直角三角形的三边长都满足这个关系呢?
学生动手,剪完三角形后量取斜边长度发现,直角边为3cm和4cm的斜边长是5cm,而直角边为6cm和7cm的斜边长不是8cm.32+42=52文字表达:直角三角形两直角边的平方和等于斜边的平方.(
若两直角边为a、b,斜边为c,则a2+b2=c2)
让学生一步一步探索,使学生亲身经历发现探索知识这一过程,培养学生语言表达能力,体会数形结合思想在教学中的应用.按学生的认知特点,由特殊到一般,便于学生接受这一知识,同时体会观察、猜想、验证结论的过程,培养学生分析解决问题的能力、语言表达能力.
动手操作亲自论证动手操作亲自论证
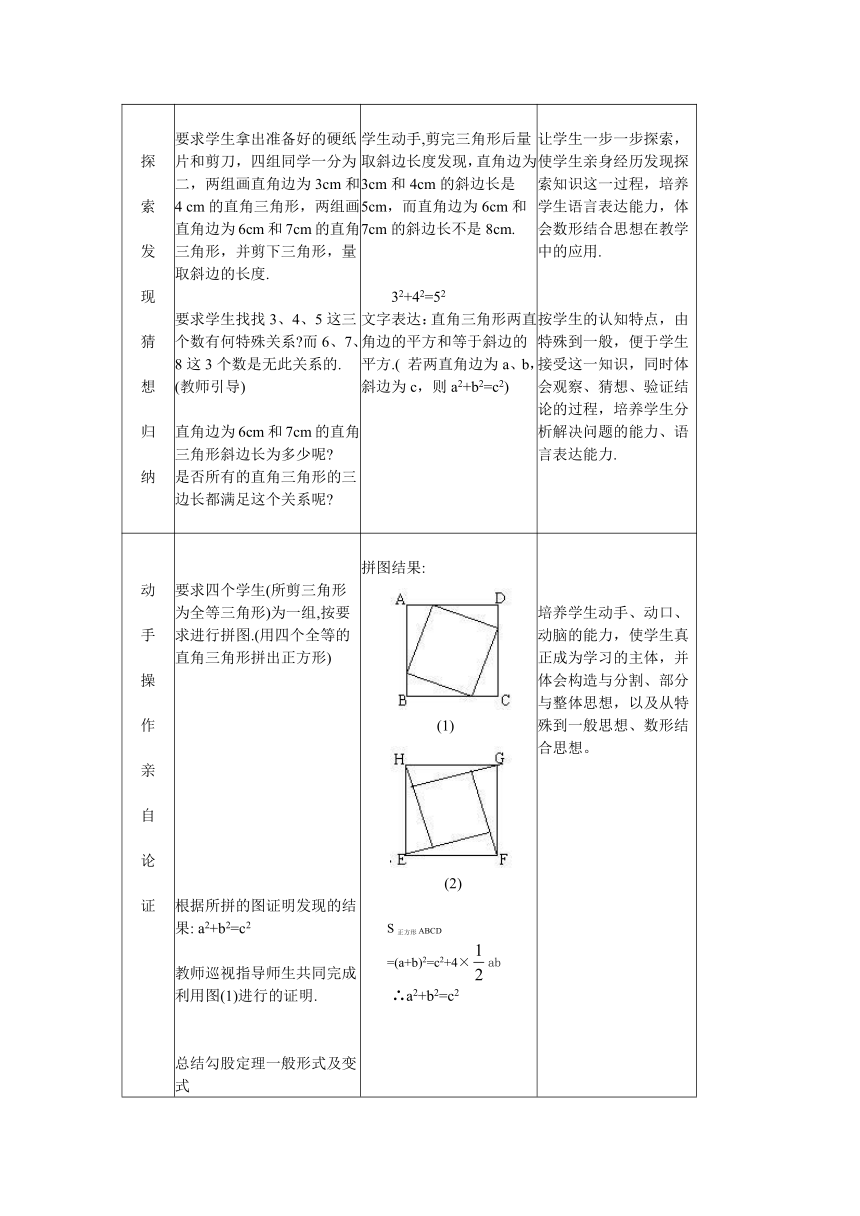
要求四个学生(所剪三角形为全等三角形)为一组,按要求进行拼图.(用四个全等的直角三角形拼出正方形)根据所拼的图证明发现的结果:
a2+b2=c2教师巡视指导师生共同完成利用图(1)进行的证明.总结勾股定理一般形式及变式勾:较短直角边股:较长直角边弦:斜边《周髀算经》记载:勾三股四弦五.对于图(2)的证明学生口述,教师补充一起完成.教师讲述勾股定理的历史,古人所作的贡献,补充其它证明的方法.
拼图结果:(1)(2)S正方形ABCD=(a+b)2=c2+4×ab∴a2+b2=c2勾股定理:直角三角形两直角边的平方和等于斜边的平方.(两直角边为a、b,斜边为c,则a2+b2=c2)用数学语言表达.若在Rt△ABC中∠C=90°,∠A,∠B∠C,所对的边分别为a,b,c,则a2+b2=c2.
培养学生动手、动口、动脑的能力,使学生真正成为学习的主体,并体会构造与分割、部分与整体思想,以及从特殊到一般思想、数形结合思想。通过介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习.
练习反馈巩固新知
一、填空1、已知在Rt△ABC中∠C=90°①若a=6,b=7,则C=______;②若a=40,b=9,则c=______;③若a=6,c=10,则b=______;④若c=25,b=15,则a=______.2、已知在Rt△ABC中,若a=6,b=8,则C=____.
独立完成练习,共同交流,巩固提高.
通过练习,得到及时的反馈,巩固新知识,弥补不足之处,升华提高.填空的第3题,进行了分类讨论思想的渗透.
练习反馈巩固新知
二、已知等边三角形ABC的边长是6cm.求:(1)高CD的长;(2)△ABC的面积
复习已学知识,结合应用新知识解决问题.
回顾反思自主总结
1、通过本节课学习你有什么收获?2、通过本节课学习你觉得还有什么疑惑?3布置作业.
学生交流新知及本节课的感受与建议.
通过反思总结经验,体验探究过程中的感受,总结不足,为今后更好地开展学习作准备.
教学目标
知识与技能
1、掌握勾股定理的内容.2、会初步运用勾股定理进行简单的计算、证明.
过程与方法
3、在探索勾股定理的过程中,让学生经历“操作—观察—猜想—归纳—验证”的数学思想,体会数形结合和特殊到一般的思想方法.
情感、态度与价值观
4、通过实验操作、探索,培养学生的学习兴趣、体验学习的乐趣.5、通过了解有关勾股定理的历史,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生奋发学习.
重点
勾股定理的掌握及其应用
难点
用面积割补法证明勾股定理
教师活动
学生活动
设计意图
创设情境提出问题
老师小时侯有过这么一个疑问:如图:从A点位置向西走3步到C点,再从C点位置向北走4步到B点位置,问从A点到B点需要走几步?若A点到C点改为6步,C点到B改为7步,则从A点到B点需要走几步?
第一个问题:5步(多数学生)第二个问题:8步(有学生这样回答,会有争议)
激发学生好奇心和求知欲,使学生带着疑问进行学习,增强学习的兴趣,同时了解生活中的数学,从生活中的实际问题导入,使学生体会数学来源于生.
探索发现猜想归纳
要求学生拿出准备好的硬纸片和剪刀,四组同学一分为二,两组画直角边为3cm和4
cm的直角三角形,两组画直角边为6cm和7cm的直角三角形,并剪下三角形,量取斜边的长度.要求学生找找3、4、5这三个数有何特殊关系?而6、7、8这3个数是无此关系的.(教师引导)直角边为6cm和7cm的直角三角形斜边长为多少呢?是否所有的直角三角形的三边长都满足这个关系呢?
学生动手,剪完三角形后量取斜边长度发现,直角边为3cm和4cm的斜边长是5cm,而直角边为6cm和7cm的斜边长不是8cm.32+42=52文字表达:直角三角形两直角边的平方和等于斜边的平方.(
若两直角边为a、b,斜边为c,则a2+b2=c2)
让学生一步一步探索,使学生亲身经历发现探索知识这一过程,培养学生语言表达能力,体会数形结合思想在教学中的应用.按学生的认知特点,由特殊到一般,便于学生接受这一知识,同时体会观察、猜想、验证结论的过程,培养学生分析解决问题的能力、语言表达能力.
动手操作亲自论证动手操作亲自论证
要求四个学生(所剪三角形为全等三角形)为一组,按要求进行拼图.(用四个全等的直角三角形拼出正方形)根据所拼的图证明发现的结果:
a2+b2=c2教师巡视指导师生共同完成利用图(1)进行的证明.总结勾股定理一般形式及变式勾:较短直角边股:较长直角边弦:斜边《周髀算经》记载:勾三股四弦五.对于图(2)的证明学生口述,教师补充一起完成.教师讲述勾股定理的历史,古人所作的贡献,补充其它证明的方法.
拼图结果:(1)(2)S正方形ABCD=(a+b)2=c2+4×ab∴a2+b2=c2勾股定理:直角三角形两直角边的平方和等于斜边的平方.(两直角边为a、b,斜边为c,则a2+b2=c2)用数学语言表达.若在Rt△ABC中∠C=90°,∠A,∠B∠C,所对的边分别为a,b,c,则a2+b2=c2.
培养学生动手、动口、动脑的能力,使学生真正成为学习的主体,并体会构造与分割、部分与整体思想,以及从特殊到一般思想、数形结合思想。通过介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习.
练习反馈巩固新知
一、填空1、已知在Rt△ABC中∠C=90°①若a=6,b=7,则C=______;②若a=40,b=9,则c=______;③若a=6,c=10,则b=______;④若c=25,b=15,则a=______.2、已知在Rt△ABC中,若a=6,b=8,则C=____.
独立完成练习,共同交流,巩固提高.
通过练习,得到及时的反馈,巩固新知识,弥补不足之处,升华提高.填空的第3题,进行了分类讨论思想的渗透.
练习反馈巩固新知
二、已知等边三角形ABC的边长是6cm.求:(1)高CD的长;(2)△ABC的面积
复习已学知识,结合应用新知识解决问题.
回顾反思自主总结
1、通过本节课学习你有什么收获?2、通过本节课学习你觉得还有什么疑惑?3布置作业.
学生交流新知及本节课的感受与建议.
通过反思总结经验,体验探究过程中的感受,总结不足,为今后更好地开展学习作准备.
