沪教版(上海)数学九年级第二学期-28.3 表示一组数据平均水平的量——平均数与加权平均数 课件(17张PPT)
文档属性
| 名称 | 沪教版(上海)数学九年级第二学期-28.3 表示一组数据平均水平的量——平均数与加权平均数 课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 246.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 23:54:14 | ||
图片预览






文档简介
表示一组数据平均水平的量
——平均数与加权平均数
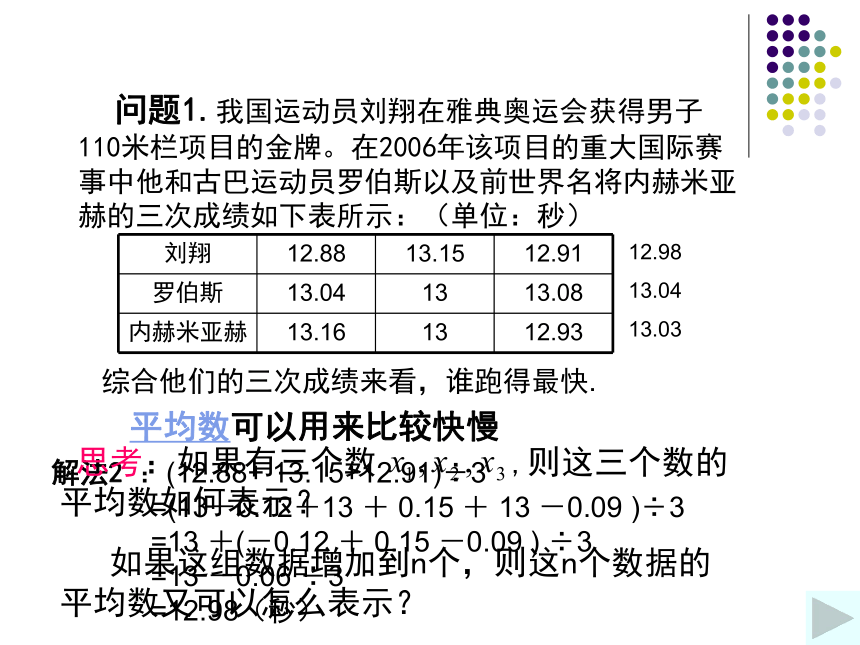
问题1.我国运动员刘翔在雅典奥运会获得男子110米栏项目的金牌。在2006年该项目的重大国际赛事中他和古巴运动员罗伯斯以及前世界名将内赫米亚赫的三次成绩如下表所示:(单位:秒)
综合他们的三次成绩来看,谁跑得最快.
平均数可以用来比较快慢
刘翔
12.88
13.15
12.91
罗伯斯
13.04
13
13.08
内赫米亚赫
13.16
13
12.93
解法2 :(12.88+ 13.15+12.91)÷3
=(13-0.12+13 + 0.15 + 13 -0.09 )÷3
=13 +(-0.12 + 0.15 -0.09 ) ÷3
=13 -0.06 ÷3
=12.98(秒)
12.98
13.04
13.03
思考:如果有三个数 ,则这三个数的平均数如何表示?
如果这组数据增加到n个,则这n个数据的平均数又可以怎么表示?
一般地,如果有n个数 ,它们的平均数记作 ,读(/eks ba: /),
这时 ①
如果一组数据所含的
都在常数a附近波动,那么可将它们写
成 , ,…, ,
再把 记作 ,可
得 ②
练一练:某大桥连续7天的车流量分别为8.0、8.3、9.1、8.5、8.2、8.4、9.0(单位:千辆/日),这七天车流量的平均数为 千辆/日。
8.5
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(1)如果把250名学生的身高叫做总体,则这16名同学的身高是一个 ,16为 .
样本
样本容量
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(2)要求这16名同学身高的平均数,可用公式: ;
(3)若用公式①,其算式是:
=
(Ⅰ)
若用公式②,可取a= .
公式①或公式②
160或165或…
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(4)根据题目数据,完成下列表格:
(5)根据上述表格,算式(Ⅰ)可以简化为:
= (Ⅱ)
身高(cm)
154
160
164
167
169
人数
1
5
1
6
3
例题1.某中学为了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(6)若将(4)题表格中的数据用字母表示:
则算式(Ⅱ)可写为:
身高(cm)
人数
=
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
更一般的,若将上述表格表示成以下形式:
则 又可以怎么表示?
身高(cm )
…
人数
…
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(7)在本题所给的16个数据中,数据154的权
是 ,164的权是 .
(8)在本例中k= ,n= ;一般的k和n之间满足的关系是:k n(填“<”或“≤”或“>”或“≥”)
5
16
≤
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(9) (“能”或“不能”)用这16位学生的平均身高估计该中学初三学生的平均身高。
能
例题1中的算法公式
记作公式③,其中
设 , ,…,
则公式③可写成 ④
其中 分别是 的权,公式③
和公式④给出的
叫作这k个数的加权平均数.
例题2.某市9月份30天中的空气污染指数统计如表所示(当w≤50时,空气质量为优;当50<w≤100时,空气质量为良;当100<w≤150时,空气质量为轻微污染)
试计算9月份空气污染的平均指数;再指出这个市在9月份的空气质量属于哪个级别.
解:利用计算器计算,得
所以这个市9月份空气平均污染指数是89.7,空气质量为良.
(w)污染指数
42
45
61
65
72
86
88
90
91
天数
2
1
3
1
1
2
3
1
2
(w)污染指数
93
100
103
104
109
113
115
117
141
天数
2
1
2
1
2
1
1
3
1
想一想,我们今天学了什么?
1.公式之间的内在联系:
2.样本平均数与总体平均数.
3. 计算器是求平均数的有力工具.
特殊
一般
②
①
④
③
(当 在常数a附近波动 )
(公式③的另一种表达方式)
作业布置
练习部分27.3(1)
——平均数与加权平均数
问题1.我国运动员刘翔在雅典奥运会获得男子110米栏项目的金牌。在2006年该项目的重大国际赛事中他和古巴运动员罗伯斯以及前世界名将内赫米亚赫的三次成绩如下表所示:(单位:秒)
综合他们的三次成绩来看,谁跑得最快.
平均数可以用来比较快慢
刘翔
12.88
13.15
12.91
罗伯斯
13.04
13
13.08
内赫米亚赫
13.16
13
12.93
解法2 :(12.88+ 13.15+12.91)÷3
=(13-0.12+13 + 0.15 + 13 -0.09 )÷3
=13 +(-0.12 + 0.15 -0.09 ) ÷3
=13 -0.06 ÷3
=12.98(秒)
12.98
13.04
13.03
思考:如果有三个数 ,则这三个数的平均数如何表示?
如果这组数据增加到n个,则这n个数据的平均数又可以怎么表示?
一般地,如果有n个数 ,它们的平均数记作 ,读(/eks ba: /),
这时 ①
如果一组数据所含的
都在常数a附近波动,那么可将它们写
成 , ,…, ,
再把 记作 ,可
得 ②
练一练:某大桥连续7天的车流量分别为8.0、8.3、9.1、8.5、8.2、8.4、9.0(单位:千辆/日),这七天车流量的平均数为 千辆/日。
8.5
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(1)如果把250名学生的身高叫做总体,则这16名同学的身高是一个 ,16为 .
样本
样本容量
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(2)要求这16名同学身高的平均数,可用公式: ;
(3)若用公式①,其算式是:
=
(Ⅰ)
若用公式②,可取a= .
公式①或公式②
160或165或…
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(4)根据题目数据,完成下列表格:
(5)根据上述表格,算式(Ⅰ)可以简化为:
= (Ⅱ)
身高(cm)
154
160
164
167
169
人数
1
5
1
6
3
例题1.某中学为了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(6)若将(4)题表格中的数据用字母表示:
则算式(Ⅱ)可写为:
身高(cm)
人数
=
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
更一般的,若将上述表格表示成以下形式:
则 又可以怎么表示?
身高(cm )
…
人数
…
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(7)在本题所给的16个数据中,数据154的权
是 ,164的权是 .
(8)在本例中k= ,n= ;一般的k和n之间满足的关系是:k n(填“<”或“≤”或“>”或“≥”)
5
16
≤
例题1.某中学为了了解初三250名学生的身高情况,随机地抽取了16名同学,测得其身高如下:(单位: cm)
164 154 160 160 167 169 160 164
160 164 167 164 160 164 164 167
(9) (“能”或“不能”)用这16位学生的平均身高估计该中学初三学生的平均身高。
能
例题1中的算法公式
记作公式③,其中
设 , ,…,
则公式③可写成 ④
其中 分别是 的权,公式③
和公式④给出的
叫作这k个数的加权平均数.
例题2.某市9月份30天中的空气污染指数统计如表所示(当w≤50时,空气质量为优;当50<w≤100时,空气质量为良;当100<w≤150时,空气质量为轻微污染)
试计算9月份空气污染的平均指数;再指出这个市在9月份的空气质量属于哪个级别.
解:利用计算器计算,得
所以这个市9月份空气平均污染指数是89.7,空气质量为良.
(w)污染指数
42
45
61
65
72
86
88
90
91
天数
2
1
3
1
1
2
3
1
2
(w)污染指数
93
100
103
104
109
113
115
117
141
天数
2
1
2
1
2
1
1
3
1
想一想,我们今天学了什么?
1.公式之间的内在联系:
2.样本平均数与总体平均数.
3. 计算器是求平均数的有力工具.
特殊
一般
②
①
④
③
(当 在常数a附近波动 )
(公式③的另一种表达方式)
作业布置
练习部分27.3(1)
