沪教版(上海)初中数学八年级第一学期 19.2 证明举例(2)-证明两边(角)相等 教案
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.2 证明举例(2)-证明两边(角)相等 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 36.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 08:51:22 | ||
图片预览

文档简介
证明举例(2)-----证明两边(角)相等
教学目标
1、认知目标:
(1)
能运用全等三角形的性质以及等角对等边,等边对等角等知识进行两边两角相等的几何证明
(2)
掌握几何证明的书写格式,强调它的条理性和严谨性。
2、能力目标:对几何问题“探究—讨论—交流—讲评”,以一题多解及变式训练培养学生灵活解题的思想,提高学生分析问题、解决问题的能力。
3、情感目标:通过独立探究、合作交流的学习过程,培养学生勤于思考的求知精神。积极动脑,自主探索的过程,正是体验数学知识发现和创造的过程。
重点和难点
1、熟练掌握证明两边两角相等的方法。
2、变式训练
教学过程设计
例1:在△ABC中,AD平分∠BAC,AD⊥BC,垂足为点D,求证:AB=AC
A
(学生口诉,教师板书)
B
D
C
小结:证明两边相等,若两边分别在两个三角形中,可利用全等三角形对应边相等来证明。
变式一:在△ABC中,AD平分∠BAC,AD⊥BC,垂足为点D,求证:∠B=∠C
两种方法
利用全等或者等边对等角
(板书过程,学生在例1的基础上进行修改)
小结:(1)证明两角相等,若两角分别在两个三角形中,可利用全等三角形对应角相等来证明。
(2)证明两角相等,若两角在同一个三角形中,可利用等边对等角来证明。
变式二:将上图点D的位置换成如右图
如图,AB=AC,DB=DC,求证:∠B=∠C
(学生口诉板书)
两种方法
连接AD
或者连接BC
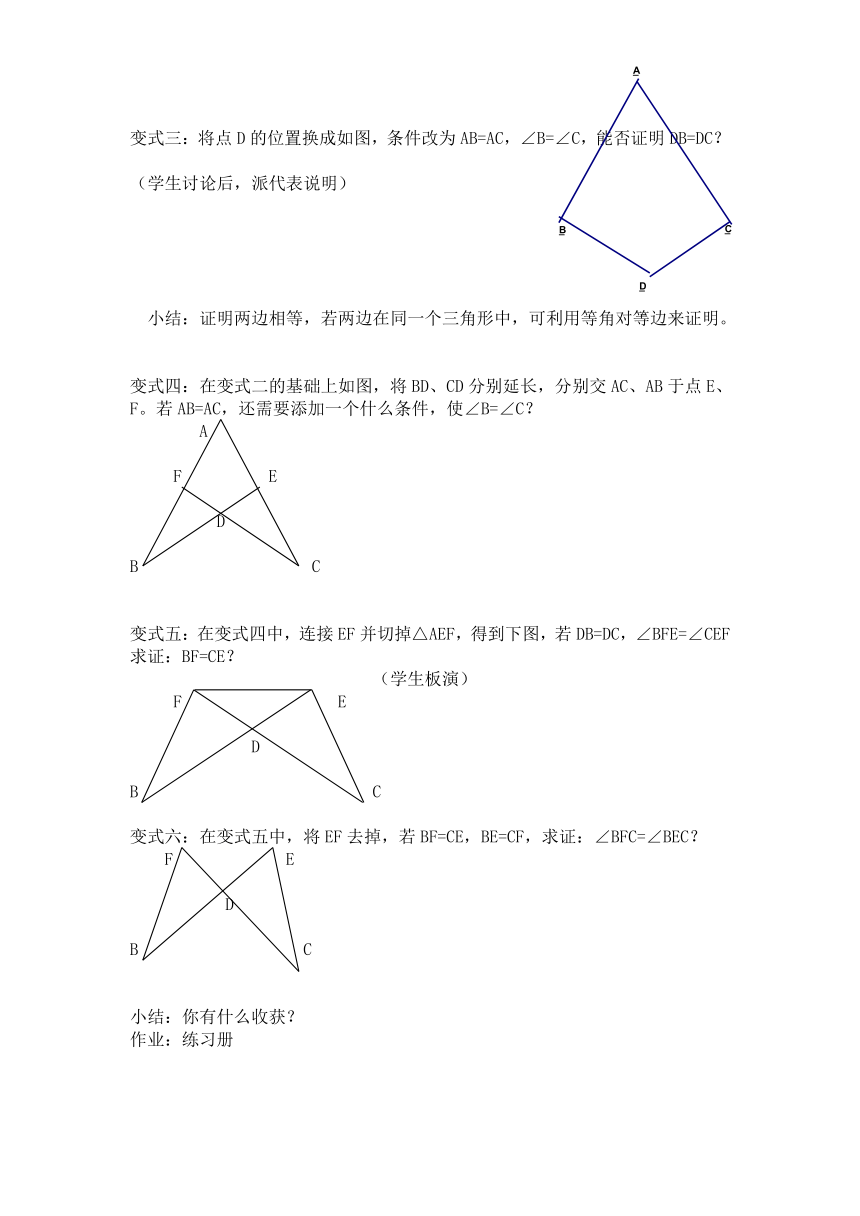
变式三:将点D的位置换成如图,条件改为AB=AC,∠B=∠C,能否证明DB=DC?
(学生讨论后,派代表说明)
小结:证明两边相等,若两边在同一个三角形中,可利用等角对等边来证明。
变式四:在变式二的基础上如图,将BD、CD分别延长,分别交AC、AB于点E、F。若AB=AC,还需要添加一个什么条件,使∠B=∠C?
A
F
E
D
B
C
变式五:在变式四中,连接EF并切掉△AEF,得到下图,若DB=DC,∠BFE=∠CEF求证:BF=CE?
(学生板演)
F
E
D
B
C
变式六:在变式五中,将EF去掉,若BF=CE,BE=CF,求证:∠BFC=∠BEC?
F
E
D
B
C
小结:你有什么收获?
作业:练习册
工
作
单
例题1:在△ABC中,AD平分∠BAC,AD⊥BC,垂足为点D,求证:AB=AC
A
B
D
C
变式一:如上图,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为点D,
求证:∠B=∠C
变式二:将点D的位置换成如图,已知,
AB=AC,DB=DC,
求证:∠B=∠C
变式三:将点D的位置换成如图条件改为AB=AC,∠B=∠C,
能否证明DB=DC
变式四:如图,将BD、CD分别延长,分别交AC、AB于点E、F。若AB=AC,
还需要添加一个什么条件,使∠B=∠C?
A
F
E
D
B
C
变式五:在变式二中,连接EF,并切掉△AEF,得到下图,若DB=DC,
∠BEF=∠CFE,求证:CE=BF?
F
E
D
B
C
变式六:在变式五中,将EF去掉,若BF=CE,BE=CF,
求证:∠BFC=∠BEC?
F
E
D
B
C
C
A
B
D
_
_
D
_
C
_
A
_
B
C
A
B
D
_
_
D
_
C
_
A
_
B
教学目标
1、认知目标:
(1)
能运用全等三角形的性质以及等角对等边,等边对等角等知识进行两边两角相等的几何证明
(2)
掌握几何证明的书写格式,强调它的条理性和严谨性。
2、能力目标:对几何问题“探究—讨论—交流—讲评”,以一题多解及变式训练培养学生灵活解题的思想,提高学生分析问题、解决问题的能力。
3、情感目标:通过独立探究、合作交流的学习过程,培养学生勤于思考的求知精神。积极动脑,自主探索的过程,正是体验数学知识发现和创造的过程。
重点和难点
1、熟练掌握证明两边两角相等的方法。
2、变式训练
教学过程设计
例1:在△ABC中,AD平分∠BAC,AD⊥BC,垂足为点D,求证:AB=AC
A
(学生口诉,教师板书)
B
D
C
小结:证明两边相等,若两边分别在两个三角形中,可利用全等三角形对应边相等来证明。
变式一:在△ABC中,AD平分∠BAC,AD⊥BC,垂足为点D,求证:∠B=∠C
两种方法
利用全等或者等边对等角
(板书过程,学生在例1的基础上进行修改)
小结:(1)证明两角相等,若两角分别在两个三角形中,可利用全等三角形对应角相等来证明。
(2)证明两角相等,若两角在同一个三角形中,可利用等边对等角来证明。
变式二:将上图点D的位置换成如右图
如图,AB=AC,DB=DC,求证:∠B=∠C
(学生口诉板书)
两种方法
连接AD
或者连接BC
变式三:将点D的位置换成如图,条件改为AB=AC,∠B=∠C,能否证明DB=DC?
(学生讨论后,派代表说明)
小结:证明两边相等,若两边在同一个三角形中,可利用等角对等边来证明。
变式四:在变式二的基础上如图,将BD、CD分别延长,分别交AC、AB于点E、F。若AB=AC,还需要添加一个什么条件,使∠B=∠C?
A
F
E
D
B
C
变式五:在变式四中,连接EF并切掉△AEF,得到下图,若DB=DC,∠BFE=∠CEF求证:BF=CE?
(学生板演)
F
E
D
B
C
变式六:在变式五中,将EF去掉,若BF=CE,BE=CF,求证:∠BFC=∠BEC?
F
E
D
B
C
小结:你有什么收获?
作业:练习册
工
作
单
例题1:在△ABC中,AD平分∠BAC,AD⊥BC,垂足为点D,求证:AB=AC
A
B
D
C
变式一:如上图,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为点D,
求证:∠B=∠C
变式二:将点D的位置换成如图,已知,
AB=AC,DB=DC,
求证:∠B=∠C
变式三:将点D的位置换成如图条件改为AB=AC,∠B=∠C,
能否证明DB=DC
变式四:如图,将BD、CD分别延长,分别交AC、AB于点E、F。若AB=AC,
还需要添加一个什么条件,使∠B=∠C?
A
F
E
D
B
C
变式五:在变式二中,连接EF,并切掉△AEF,得到下图,若DB=DC,
∠BEF=∠CFE,求证:CE=BF?
F
E
D
B
C
变式六:在变式五中,将EF去掉,若BF=CE,BE=CF,
求证:∠BFC=∠BEC?
F
E
D
B
C
C
A
B
D
_
_
D
_
C
_
A
_
B
C
A
B
D
_
_
D
_
C
_
A
_
B
