人教版八年级上册第十四章整式的乘法与因式分解 3课时 幂的乘方课件(24张PPT)
文档属性
| 名称 | 人教版八年级上册第十四章整式的乘法与因式分解 3课时 幂的乘方课件(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 357.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:00:00 | ||
图片预览



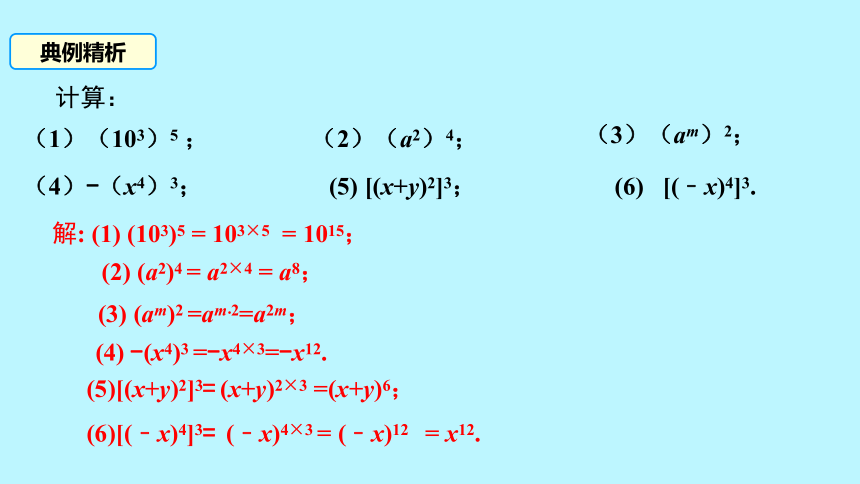



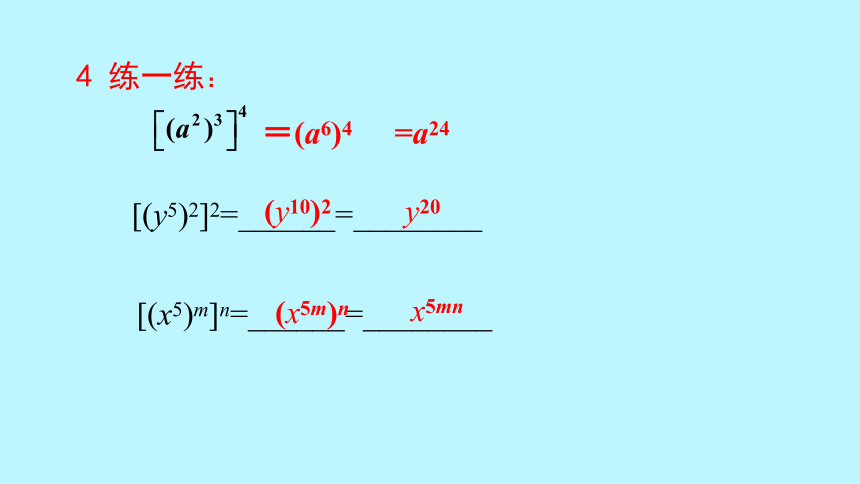
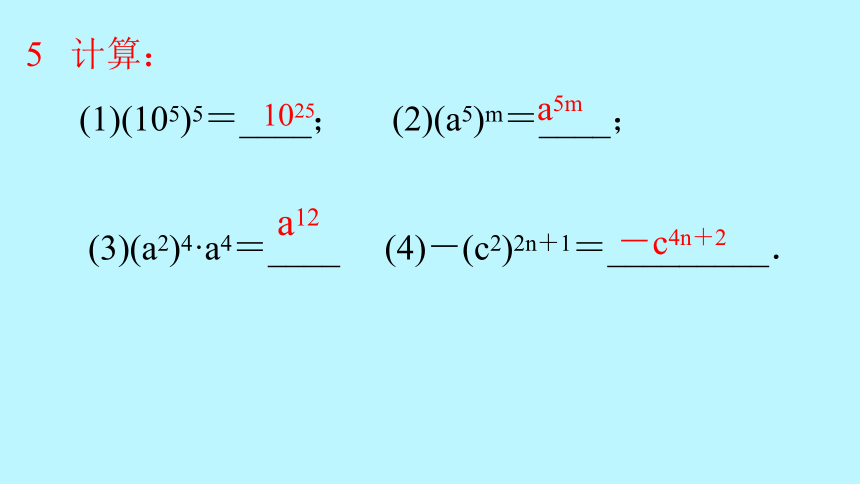
文档简介
14.1 整式的乘法
14.1.2 幂的乘方
幂的乘方法则
(am)n= amn
(m,n都是正整数)
即幂的乘方,底数_ , 指数____.
不变
相乘
n个am
m m m
a a a ‥‥‥
=
n个m
m+m+m
‥‥‥
精彩回放
精彩点拨
幂的乘方法则:(am)n=____(m,n都是正整数).
即幂的乘方,____________________.
amn
底数不变,指数相乘
计算:
(1)(103)5 ;
解: (1) (103)5 = 103×5 = 1015;
(2) (a2)4 = a2×4 = a8;
(3) (am)2 =am·2=a2m;
(3)(am)2;
(2)(a2)4;
典例精析
(4)-(x4)3;
(4) -(x4)3 =-x4×3=-x12.
(6) [(﹣x)4]3.
(5) [(x+y)2]3;
(5)[(x+y)2]3= (x+y)2×3 =(x+y)6;
(6)[(﹣x)4]3= (﹣x)4×3 = (﹣x)12 = x12.
1 选择
1.(3分)(漯河期末)计算(a2)3的结果是( )
A.a5 B.a6 C.a8 D.3a2
2.(3分)(2017·安徽)计算(-a3)2的结果是( )
A.a6 B.-a6 C.-a5 D.a5
B
A
(-a5)2表示2个-a5相乘,结果没有负号.
2 比一比
(-a2)5和(-a5)2的结果相同吗?为什么?
不相同.
(-a2)5表示5个-a2相乘,其结果带有负号.
n为偶数
n为奇偶数
3.下列运算正确的是( )
A.a3·a3=2a6
B.a3+a3=2a6
C.(a3)2=a6
D.a6·a2=a3
C
=(a6)4
=a24
[(y5)2]2=______=________
[(x5)m]n=______=________
4 练一练:
(y10)2
y20
(x5m)n
x5mn
5 计算:
(1)(105)5=____; (2)(a5)m=____;
(3)(a2)4·a4=____ (4)-(c2)2n+1=_________.
1025
a5m
a12
-c4n+2
6 计算:
(1) (x4)3·x6;
(2) a2(-a)2(-a2)3+a10.
解: (1) (x4)3·x6
=x12·x6
= x18;
(2) a2(-a)2(-a2)3+a10
= -a2·a2·a6+a10
= -a10+a10 = 0.
7 计算: (1)(x2)4+(x3)2·x2;
解:2x8
(2)5(a4)3-15(a2)6.
解:-10a12
8 已知10m=3,10n=2,求下列各式的值.
(1)103m;(2)102n;(3)103m+2n.
解:(1)103m=(10m)3=33=27;
(2)102n=(10n)2=22=4;
(3)103m+2n=103m×102n=27×4=108.
9 选择
若3×9m×27m=321,则m的值为( )
A.3 B.4 C.5 D.6
若a2n=3,则a6n=____.
已知xm=2,xn=3,则x2m+3n的值为____.
B
27
108
(1)已知x2n=3,求(x3n)4的值;
(2)已知2x+5y-3=0,求4x·32y的值.
解:(1) (x3n)4=x12n=(x2n)6=36=729.
(2) ∵2x+5y-3=0,
∴2x+5y=3,
∴4x·32y=(22)x·(25)y=22x·25y=22x+5y=23=8.
10 变式训练
11 选择
B
10
12 比较3500,4400,5300的大小.
解:3500=(35)100=243100,
4400=(44)100=256100,
5300=(53)100=125100.
∵256100>243100>125100,
∴4400>3500>5300.
13 练习
1.(x4)2等于 ( )
A.x6 B.x8
C.x16 D.2x4
B
2.下列各式的括号内,应填入b4的是( )
A.b12=( )8 B.b12=( )6
C.b12=( )3 D.b12=( )2
C
14 计算:
(1)(a2)9+(a4·a2)3+[(a3)2]3;
解:原式=a18+(a6)3+(a6)3
=a18+a18+a18=3a18
(2)212×415×810.
解:原式=212×(22)15×(23)10=212×230×230=272
12.(5分)已知2x+5y-3=0,求4x·32y的值.
解:4x·32y=(22)x·(25)y=22x·25y=22x+5y=23=8
15 选择
下列计算中,错误的是( )
A.[(a+b)2]3=(a+b)6
B.[(a+b)2]5=(a+b)7
C.[(a-b)3]n=(a-b)3n
D.[(a-b)3]2=(a-b)6
B
4.如果(9n)2=312,那么n的值是( )
A.4 B.3
C.2 D.1
B
16.计算:
(1)(102)8;
(2)(xm)2;
(3)[(-a)3]5
(4)-(x2)m.
解:(1)(102)8=1016.
(2)(xm)2=x2m.
(3)[(-a)3]5=(-a)15=-a15.
(4)-(x2)m=-x2m.
17.计算:
(1)5(a3)4-13(a6)2;
(2)7x4·x5·(-x)7+5(x4)4-(x8)2;
(3)[(x+y)3]6+[-(x+y)2]9.
解:(1)原式=5a12-13a12=-8a12.
(2)原式=-7x9·x7+5x16-x16=-3x16.
(3)原式=(x+y)18-(x+y)18=0.
18. 已知3x+4y-5=0,求27x·81y的值.
解:∵3x+4y-5=0,
∴3x+4y=5,
∴27x·81y=(33)x·(34)y
=33x·34y
=33x+4y
=35
=243.
【综合运用】
19.阅读下列解题过程:
试比较2100与375的大小.
解:2100=(24)25=1625,375=(33)25=2725,
而16<27,∴1625<2725,∴2100<375.
请根据上述解题方法,比较3555,4444,5333的大小.
解:3555=(35)111=243111,4444=(44)111=256111,5333=(53)111=125111,
而125<243<256,∴125111<243111<256111,∴5333<3555<4444
14.1.2 幂的乘方
幂的乘方法则
(am)n= amn
(m,n都是正整数)
即幂的乘方,底数_ , 指数____.
不变
相乘
n个am
m m m
a a a ‥‥‥
=
n个m
m+m+m
‥‥‥
精彩回放
精彩点拨
幂的乘方法则:(am)n=____(m,n都是正整数).
即幂的乘方,____________________.
amn
底数不变,指数相乘
计算:
(1)(103)5 ;
解: (1) (103)5 = 103×5 = 1015;
(2) (a2)4 = a2×4 = a8;
(3) (am)2 =am·2=a2m;
(3)(am)2;
(2)(a2)4;
典例精析
(4)-(x4)3;
(4) -(x4)3 =-x4×3=-x12.
(6) [(﹣x)4]3.
(5) [(x+y)2]3;
(5)[(x+y)2]3= (x+y)2×3 =(x+y)6;
(6)[(﹣x)4]3= (﹣x)4×3 = (﹣x)12 = x12.
1 选择
1.(3分)(漯河期末)计算(a2)3的结果是( )
A.a5 B.a6 C.a8 D.3a2
2.(3分)(2017·安徽)计算(-a3)2的结果是( )
A.a6 B.-a6 C.-a5 D.a5
B
A
(-a5)2表示2个-a5相乘,结果没有负号.
2 比一比
(-a2)5和(-a5)2的结果相同吗?为什么?
不相同.
(-a2)5表示5个-a2相乘,其结果带有负号.
n为偶数
n为奇偶数
3.下列运算正确的是( )
A.a3·a3=2a6
B.a3+a3=2a6
C.(a3)2=a6
D.a6·a2=a3
C
=(a6)4
=a24
[(y5)2]2=______=________
[(x5)m]n=______=________
4 练一练:
(y10)2
y20
(x5m)n
x5mn
5 计算:
(1)(105)5=____; (2)(a5)m=____;
(3)(a2)4·a4=____ (4)-(c2)2n+1=_________.
1025
a5m
a12
-c4n+2
6 计算:
(1) (x4)3·x6;
(2) a2(-a)2(-a2)3+a10.
解: (1) (x4)3·x6
=x12·x6
= x18;
(2) a2(-a)2(-a2)3+a10
= -a2·a2·a6+a10
= -a10+a10 = 0.
7 计算: (1)(x2)4+(x3)2·x2;
解:2x8
(2)5(a4)3-15(a2)6.
解:-10a12
8 已知10m=3,10n=2,求下列各式的值.
(1)103m;(2)102n;(3)103m+2n.
解:(1)103m=(10m)3=33=27;
(2)102n=(10n)2=22=4;
(3)103m+2n=103m×102n=27×4=108.
9 选择
若3×9m×27m=321,则m的值为( )
A.3 B.4 C.5 D.6
若a2n=3,则a6n=____.
已知xm=2,xn=3,则x2m+3n的值为____.
B
27
108
(1)已知x2n=3,求(x3n)4的值;
(2)已知2x+5y-3=0,求4x·32y的值.
解:(1) (x3n)4=x12n=(x2n)6=36=729.
(2) ∵2x+5y-3=0,
∴2x+5y=3,
∴4x·32y=(22)x·(25)y=22x·25y=22x+5y=23=8.
10 变式训练
11 选择
B
10
12 比较3500,4400,5300的大小.
解:3500=(35)100=243100,
4400=(44)100=256100,
5300=(53)100=125100.
∵256100>243100>125100,
∴4400>3500>5300.
13 练习
1.(x4)2等于 ( )
A.x6 B.x8
C.x16 D.2x4
B
2.下列各式的括号内,应填入b4的是( )
A.b12=( )8 B.b12=( )6
C.b12=( )3 D.b12=( )2
C
14 计算:
(1)(a2)9+(a4·a2)3+[(a3)2]3;
解:原式=a18+(a6)3+(a6)3
=a18+a18+a18=3a18
(2)212×415×810.
解:原式=212×(22)15×(23)10=212×230×230=272
12.(5分)已知2x+5y-3=0,求4x·32y的值.
解:4x·32y=(22)x·(25)y=22x·25y=22x+5y=23=8
15 选择
下列计算中,错误的是( )
A.[(a+b)2]3=(a+b)6
B.[(a+b)2]5=(a+b)7
C.[(a-b)3]n=(a-b)3n
D.[(a-b)3]2=(a-b)6
B
4.如果(9n)2=312,那么n的值是( )
A.4 B.3
C.2 D.1
B
16.计算:
(1)(102)8;
(2)(xm)2;
(3)[(-a)3]5
(4)-(x2)m.
解:(1)(102)8=1016.
(2)(xm)2=x2m.
(3)[(-a)3]5=(-a)15=-a15.
(4)-(x2)m=-x2m.
17.计算:
(1)5(a3)4-13(a6)2;
(2)7x4·x5·(-x)7+5(x4)4-(x8)2;
(3)[(x+y)3]6+[-(x+y)2]9.
解:(1)原式=5a12-13a12=-8a12.
(2)原式=-7x9·x7+5x16-x16=-3x16.
(3)原式=(x+y)18-(x+y)18=0.
18. 已知3x+4y-5=0,求27x·81y的值.
解:∵3x+4y-5=0,
∴3x+4y=5,
∴27x·81y=(33)x·(34)y
=33x·34y
=33x+4y
=35
=243.
【综合运用】
19.阅读下列解题过程:
试比较2100与375的大小.
解:2100=(24)25=1625,375=(33)25=2725,
而16<27,∴1625<2725,∴2100<375.
请根据上述解题方法,比较3555,4444,5333的大小.
解:3555=(35)111=243111,4444=(44)111=256111,5333=(53)111=125111,
而125<243<256,∴125111<243111<256111,∴5333<3555<4444
