人教版八年级数学下册课件:17.2 第2课时 勾股定理及其逆定理的综合应用(16张)
文档属性
| 名称 | 人教版八年级数学下册课件:17.2 第2课时 勾股定理及其逆定理的综合应用(16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 07:56:23 | ||
图片预览





文档简介
第十七章 勾股定理
17.2 第2课时 勾股定理及其逆定理的综合应用
知识回顾
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形.
a2 + b2 = c2
勾股定理的逆定理
互逆定理
例题讲解
例1 某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定的方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
分析:在图中可以看到,由于“远航”号的航向已知,如果求出两艘轮船的航向所成的角,就能知道“海天”号的航向了.
解:根据题意,PQ =16×1.5 = 24,PR=12×1.5 = 18,
QR=30.
因为 242+182=302,即 PQ2+PR2=QR2,
所以∠QPR= 90°.
由“远航”号沿东北方向航行可知,∠1=45°.
因此∠2=45°,即“海天”号沿西北方向航行.
获取新知
知识点一:勾股定理的逆定理的应用
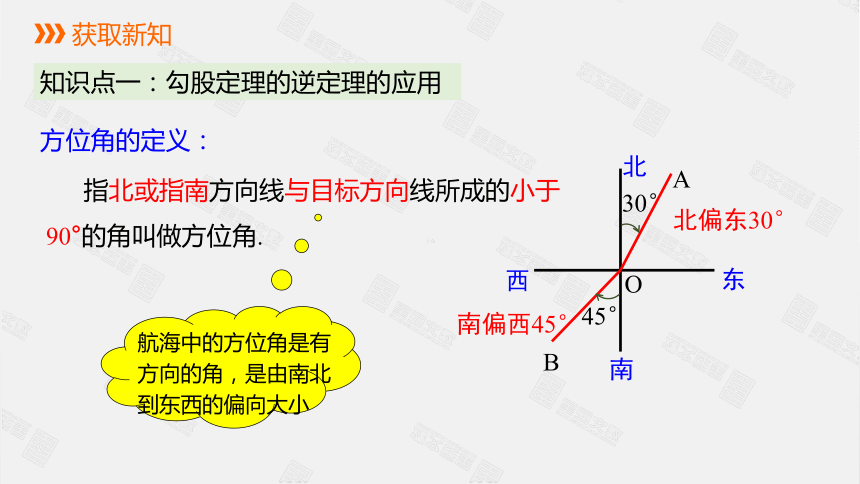
方位角的定义:
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角.
30°
45°
B
O
A
东
西
北
南
北偏东30°
南偏西45°
航海中的方位角是有方向的角,是由南北到东西的偏向大小
东
西
北
O
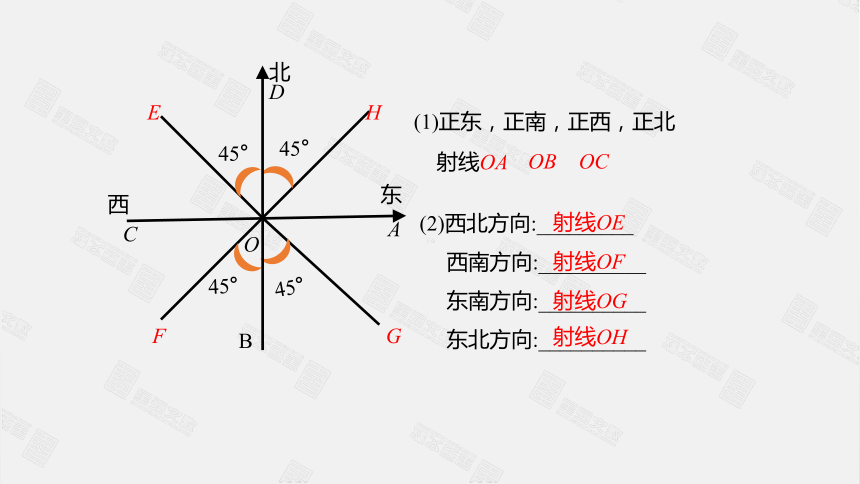
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
例题讲解
例2 如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
A
D
B
C
3
4
13
12
分析:不规则图形的面积问题,多用“割补法”,对于本题显然是用“分割法”更合适些,所以问题就转化为求三角形ACD的面积问题了,即三角形的形状问题
解:连接AC.
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
A
D
B
C
3
4
13
12
随堂演练
1.有五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )
C
2.如图,每个小正方形的边长均为1,A,B,C均为小正方形的顶点,则∠ABC的度数为( ).
A.90° B.60° C.45° D.30°
C
3. 一根电线杆高12 m,为了安全起见,在电线杆顶部到与电线杆底部水平距离5 m处加一根拉线.拉线工人发现所用线长为13.2米(不计捆缚部分),则电线杆与地面________.(填“垂直”或“不垂直”)
不垂直
4. 如图,在△ABC中,D为BC上一点,且BD=3,CD=AB=5,AD=4,则AC=_____.
5. 某小区的一所健身中心的平面图如图所示,活动区是面积为200 m2的长方形,其长为20 m,餐饮区是一个半圆形,面积为4.5π m2,休息区是一个三角形,边AE=8 m,求休息区的面积.
解:∵S长方形ABCD=200 m2,AB=20 m,∴AD=10 m.
∴DE=6 m.
又∵AE=8 m,
∴DE2+AE2=AD2,
∴△AED为直角三角形,
∴△AED的面积为 ×6×8=24(m2),
即休息区的面积是24 m2.
6. 如图,在△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13,求阴影部分的面积.
解:在Rt△ABC中,
∵∠B=90°,AB=3,BC=4,
又∵CD=12,AD=13,
∴AC2+CD2=52+122=169,AD2=132=169,
∴AD2=AC2+CD2,
∴∠ACD=90°.
∴S阴影=S△ACD-S△ABC= AC·CD- AB·BC=24
课堂小结
勾股定理的逆定理的应用
应用
航海问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆
定理来解决问题
与勾股定理结合解决不规则图形等问题
17.2 第2课时 勾股定理及其逆定理的综合应用
知识回顾
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形.
a2 + b2 = c2
勾股定理的逆定理
互逆定理
例题讲解
例1 某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定的方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
分析:在图中可以看到,由于“远航”号的航向已知,如果求出两艘轮船的航向所成的角,就能知道“海天”号的航向了.
解:根据题意,PQ =16×1.5 = 24,PR=12×1.5 = 18,
QR=30.
因为 242+182=302,即 PQ2+PR2=QR2,
所以∠QPR= 90°.
由“远航”号沿东北方向航行可知,∠1=45°.
因此∠2=45°,即“海天”号沿西北方向航行.
获取新知
知识点一:勾股定理的逆定理的应用
方位角的定义:
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角.
30°
45°
B
O
A
东
西
北
南
北偏东30°
南偏西45°
航海中的方位角是有方向的角,是由南北到东西的偏向大小
东
西
北
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
例题讲解
例2 如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
A
D
B
C
3
4
13
12
分析:不规则图形的面积问题,多用“割补法”,对于本题显然是用“分割法”更合适些,所以问题就转化为求三角形ACD的面积问题了,即三角形的形状问题
解:连接AC.
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
A
D
B
C
3
4
13
12
随堂演练
1.有五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )
C
2.如图,每个小正方形的边长均为1,A,B,C均为小正方形的顶点,则∠ABC的度数为( ).
A.90° B.60° C.45° D.30°
C
3. 一根电线杆高12 m,为了安全起见,在电线杆顶部到与电线杆底部水平距离5 m处加一根拉线.拉线工人发现所用线长为13.2米(不计捆缚部分),则电线杆与地面________.(填“垂直”或“不垂直”)
不垂直
4. 如图,在△ABC中,D为BC上一点,且BD=3,CD=AB=5,AD=4,则AC=_____.
5. 某小区的一所健身中心的平面图如图所示,活动区是面积为200 m2的长方形,其长为20 m,餐饮区是一个半圆形,面积为4.5π m2,休息区是一个三角形,边AE=8 m,求休息区的面积.
解:∵S长方形ABCD=200 m2,AB=20 m,∴AD=10 m.
∴DE=6 m.
又∵AE=8 m,
∴DE2+AE2=AD2,
∴△AED为直角三角形,
∴△AED的面积为 ×6×8=24(m2),
即休息区的面积是24 m2.
6. 如图,在△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13,求阴影部分的面积.
解:在Rt△ABC中,
∵∠B=90°,AB=3,BC=4,
又∵CD=12,AD=13,
∴AC2+CD2=52+122=169,AD2=132=169,
∴AD2=AC2+CD2,
∴∠ACD=90°.
∴S阴影=S△ACD-S△ABC= AC·CD- AB·BC=24
课堂小结
勾股定理的逆定理的应用
应用
航海问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆
定理来解决问题
与勾股定理结合解决不规则图形等问题
