人教版数学八年级上册14.1.4单项式乘以单项式 课件(19张PPT)
文档属性
| 名称 | 人教版数学八年级上册14.1.4单项式乘以单项式 课件(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 720.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 23:59:36 | ||
图片预览




文档简介
看谁算得又快又准!
(1)105×102 (2)c5?c2
问题:光的速度约为3×105千米/秒,太阳光照射到地球上需要的时间大约是5×102秒,你知道地球与太阳的距离约是多少千米吗?
(3×105)×(5×102)
学习目标
1、明确单项式乘法的依据和法则。
2、能熟练进行单项式乘以单项式的运算。
看谁算得又快又准!
(1)105×102 (2)c5?c2
问题:光的速度约为3×105千米/秒,太阳光照射到地球上需要的时间大约是5×102秒,你知道地球与太阳的距离约是多少千米吗?
(3×105)×(5×102)
地球与太阳的距离约是:
(3×105)×(5×102)
=(3 ×5) ×(105 ×102)
=15 ×107
=1.5 ×108(千米)
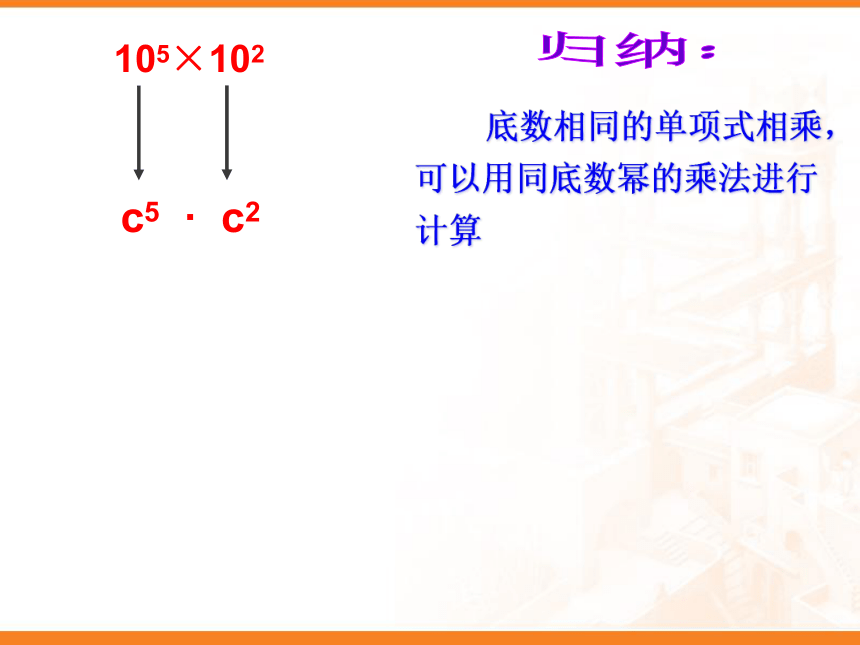
底数相同的单项式相乘,可以用同底数幂的乘法进行计算
c5 · c2
105×102
3c5?5c2=(3?5)?(c5?c2)
=15c5+2=15c7.
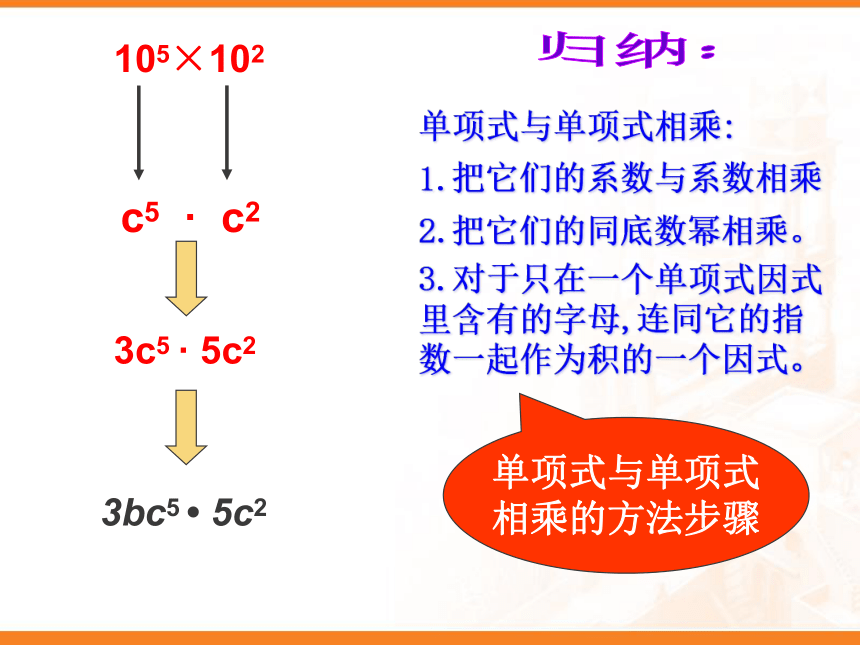
单项式与单项式相乘:
1.把它们的系数与系数相乘
2.把它们的同底数幂相乘。
3c5 · 5c2
c5 · c2
105×102
(1) 3x2·5x3
(2) 4y· (-2y2)
(3) -5a4· (-a2)
3c5 · 5c2
c5 · c2
105×102
3bc5 ? 5c2
3.对于只在一个单项式因式里含有的字母,连同它的指数一起作为积的一个因式。
单项式与单项式相乘:
1.把它们的系数与系数相乘
2.把它们的同底数幂相乘。
单项式与单项式
相乘的方法步骤
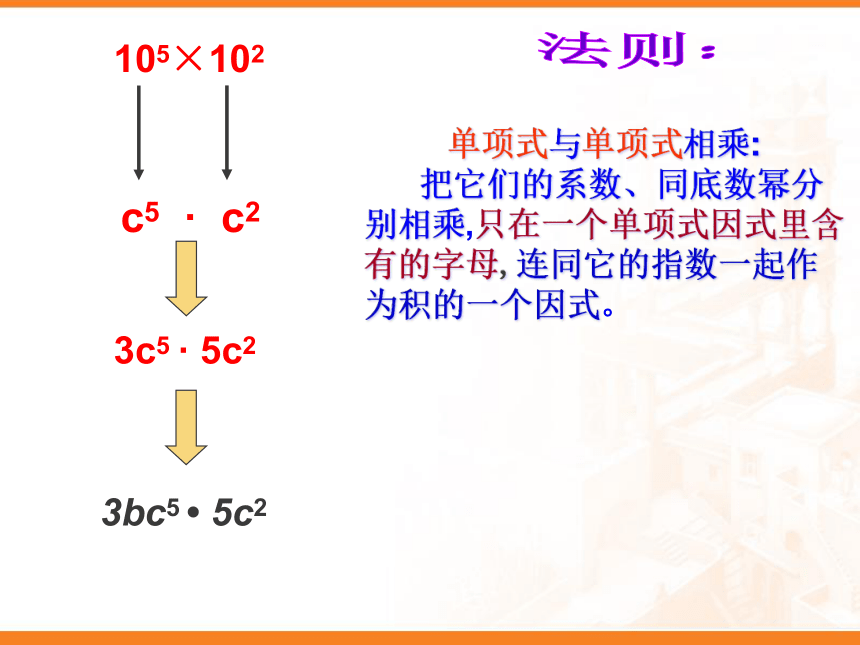
单项式与单项式相乘:
把它们的系数、同底数幂分别相乘,只在一个单项式因式里含有的字母,连同它的指数一起作为积的一个因式。
3c5 · 5c2
c5 · c2
105×102
3bc5 ? 5c2
×
×
×
×
(1)4a2 ?2a4 = 8a8 ( )
(2)6a3 ?5a2=11a5 ( )
(3)(-7a)?(-3a3) =-21a4 ( )
(4)3a2b ?4a3=12a5 ( )
系数相乘
同底数幂的乘法,底数不变,指数相加
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
求系数的积,应注意符号
(1)3bc5?5a
(2)(-a2b)?ac
(3)(-x3y)?(-4x)
看谁掌握的牢:
(4)xy?(-2xz2)
例1. 计算:
解: 原式= [(-5)×(-3)](a2?a)b
= 15a3b
(1) (-5a2b)(-3a);
3.对于只在一个单项式因式里含有的字母,连同它的指数一起作为积的一个因式。
单项式与单项式相乘:
1.把它们的系数与系数相乘
2.把它们的同底数幂相乘。
(2) (2x)3(-5xy2)
=8x3(-5xy2)
=[8×(-5)](x3?x)y2
=-40x4y2
有积的乘方怎么办?运算时应先算什么?
(2) (2x)3(-5xy2).
有乘方运算,先算乘方,再算单项式相乘。
注意:
例1. 计算:
(2) (2x)3(-5xy2)
=8x3(-5xy2)
=[8×(-5)](x3?x)y2
=-40x4y2
(2) (2x)3(-5xy2).
例1. 计算:
(1)4y?(-2xy2)
(2)(-3x)2?4x2
(3)(-2a)3?(-3a)2
(4)-2a?(-3a)?ab2
练习:
单项式与单项式相乘:把它们的系数、同底数幂分别相乘,只在一个单项式因式里含有的字母,连同它的指数一起作为积的一个因式。
一个法则:
一个方法:
单项式与单项式相乘的方法步骤:
(1)各单项式的系数相乘;
(2)底数相同的幂分别相乘,用它们的指数的和作为积里这个字母的指数,
(3)只在一个单项式因式里含有的字母,
连同它的指数一起作为积的一个因式.
一种思想:
由特殊到一般的思想
(1)求系数的积,应注意符号;
(2)相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;
(3)只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏;
(4)单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;
(5)单项式乘法的法则对于三个以上的单项式相乘同样适用。
单项式与单项式相乘时应注意:
1、下列计算中,正确的是( )
A、2a3·3a2=6a6 B、4x3·2x5=8x8
C、3x·3x4=9x4 D、5x7·5x7=10x14
2、下列运算正确的是( )
A、X2·X3=X6 B、X2+X2=2X4
C、(-2X)2=-4X2 D、(-2X2)(-3X3)=6x5
B
D
3.下面的计算对不 对?如果不对,怎样改正?
⑴
⑷
⑶
⑵
⑸
-9x3y2
a2bXn+2
a6nb6n
2?1012
4.计算:
已知
求m、n的值。
由此可得:
2m+2=4
3m+2n+2=9
解得:
m=1
n=2
∴m、n得值分别是m=1,n=2.
5.
作业:
课本第104页
习题14.1 第3题
(1)105×102 (2)c5?c2
问题:光的速度约为3×105千米/秒,太阳光照射到地球上需要的时间大约是5×102秒,你知道地球与太阳的距离约是多少千米吗?
(3×105)×(5×102)
学习目标
1、明确单项式乘法的依据和法则。
2、能熟练进行单项式乘以单项式的运算。
看谁算得又快又准!
(1)105×102 (2)c5?c2
问题:光的速度约为3×105千米/秒,太阳光照射到地球上需要的时间大约是5×102秒,你知道地球与太阳的距离约是多少千米吗?
(3×105)×(5×102)
地球与太阳的距离约是:
(3×105)×(5×102)
=(3 ×5) ×(105 ×102)
=15 ×107
=1.5 ×108(千米)
底数相同的单项式相乘,可以用同底数幂的乘法进行计算
c5 · c2
105×102
3c5?5c2=(3?5)?(c5?c2)
=15c5+2=15c7.
单项式与单项式相乘:
1.把它们的系数与系数相乘
2.把它们的同底数幂相乘。
3c5 · 5c2
c5 · c2
105×102
(1) 3x2·5x3
(2) 4y· (-2y2)
(3) -5a4· (-a2)
3c5 · 5c2
c5 · c2
105×102
3bc5 ? 5c2
3.对于只在一个单项式因式里含有的字母,连同它的指数一起作为积的一个因式。
单项式与单项式相乘:
1.把它们的系数与系数相乘
2.把它们的同底数幂相乘。
单项式与单项式
相乘的方法步骤
单项式与单项式相乘:
把它们的系数、同底数幂分别相乘,只在一个单项式因式里含有的字母,连同它的指数一起作为积的一个因式。
3c5 · 5c2
c5 · c2
105×102
3bc5 ? 5c2
×
×
×
×
(1)4a2 ?2a4 = 8a8 ( )
(2)6a3 ?5a2=11a5 ( )
(3)(-7a)?(-3a3) =-21a4 ( )
(4)3a2b ?4a3=12a5 ( )
系数相乘
同底数幂的乘法,底数不变,指数相加
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
求系数的积,应注意符号
(1)3bc5?5a
(2)(-a2b)?ac
(3)(-x3y)?(-4x)
看谁掌握的牢:
(4)xy?(-2xz2)
例1. 计算:
解: 原式= [(-5)×(-3)](a2?a)b
= 15a3b
(1) (-5a2b)(-3a);
3.对于只在一个单项式因式里含有的字母,连同它的指数一起作为积的一个因式。
单项式与单项式相乘:
1.把它们的系数与系数相乘
2.把它们的同底数幂相乘。
(2) (2x)3(-5xy2)
=8x3(-5xy2)
=[8×(-5)](x3?x)y2
=-40x4y2
有积的乘方怎么办?运算时应先算什么?
(2) (2x)3(-5xy2).
有乘方运算,先算乘方,再算单项式相乘。
注意:
例1. 计算:
(2) (2x)3(-5xy2)
=8x3(-5xy2)
=[8×(-5)](x3?x)y2
=-40x4y2
(2) (2x)3(-5xy2).
例1. 计算:
(1)4y?(-2xy2)
(2)(-3x)2?4x2
(3)(-2a)3?(-3a)2
(4)-2a?(-3a)?ab2
练习:
单项式与单项式相乘:把它们的系数、同底数幂分别相乘,只在一个单项式因式里含有的字母,连同它的指数一起作为积的一个因式。
一个法则:
一个方法:
单项式与单项式相乘的方法步骤:
(1)各单项式的系数相乘;
(2)底数相同的幂分别相乘,用它们的指数的和作为积里这个字母的指数,
(3)只在一个单项式因式里含有的字母,
连同它的指数一起作为积的一个因式.
一种思想:
由特殊到一般的思想
(1)求系数的积,应注意符号;
(2)相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;
(3)只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏;
(4)单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;
(5)单项式乘法的法则对于三个以上的单项式相乘同样适用。
单项式与单项式相乘时应注意:
1、下列计算中,正确的是( )
A、2a3·3a2=6a6 B、4x3·2x5=8x8
C、3x·3x4=9x4 D、5x7·5x7=10x14
2、下列运算正确的是( )
A、X2·X3=X6 B、X2+X2=2X4
C、(-2X)2=-4X2 D、(-2X2)(-3X3)=6x5
B
D
3.下面的计算对不 对?如果不对,怎样改正?
⑴
⑷
⑶
⑵
⑸
-9x3y2
a2bXn+2
a6nb6n
2?1012
4.计算:
已知
求m、n的值。
由此可得:
2m+2=4
3m+2n+2=9
解得:
m=1
n=2
∴m、n得值分别是m=1,n=2.
5.
作业:
课本第104页
习题14.1 第3题
