人教版数学八年级上册15.3.2分式方程解应用题 课件(20张)
文档属性
| 名称 | 人教版数学八年级上册15.3.2分式方程解应用题 课件(20张) |  | |
| 格式 | ppt | ||
| 文件大小 | 766.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 08:04:04 | ||
图片预览








文档简介
分式方程(3)
——分式方程解应用题
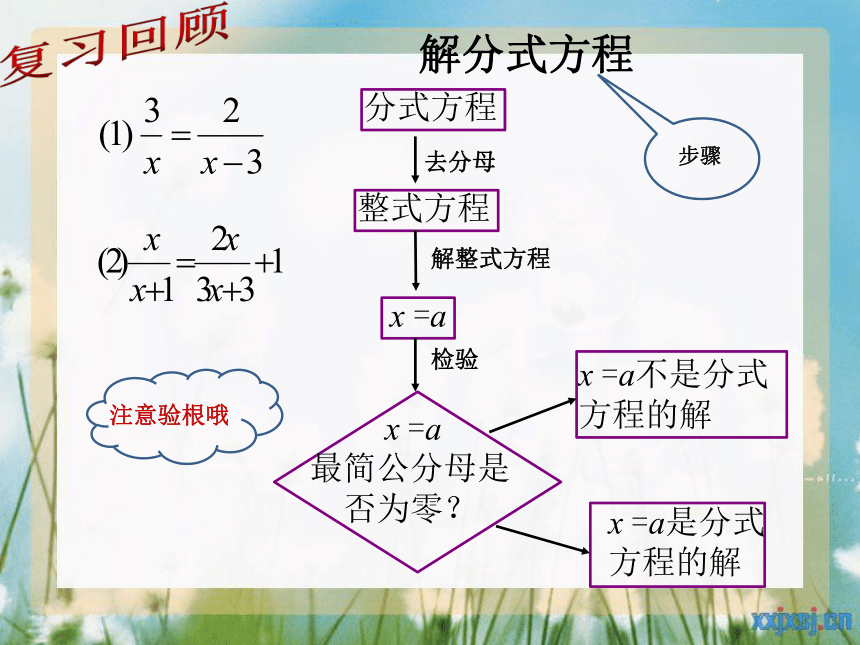
解分式方程
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a
最简公分母是
否为零?
注意验根哦
步骤
列一元一次方程解应用题的步骤是什么?
1.审题;
2.设未知数;
3.列方程;
4.解方程;
5.作答。
1、(1)工程问题基本公式:
(2)某项工程甲独做10天完成,则每天完成
,乙独做6天完成这项工程的 ,则
需 天完成 ,每天完成 。
工作量=工时×工效,
(3)某公司需要600台机器,甲工厂12天可完成,则甲工厂每天生产 台,乙工厂每天比甲多生产10台,则乙工厂 天可以完成。
50
10
此时,不知具体的工作总量,常常设为“1”。
此时,知道工作总量是600台,在解决问题时常用具体的工作量。
2、(1)行程问题基本公式:路程=速度×时间,
常用字母:路程——S,速度——V,时间——t
(2)某汽车从甲地开往乙地,每小时行驶50千米,6小时可以到达,如果要提前1小时到达,则每小时行驶 千米。
60
例3 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
分析:常常设工作总量为“1”,甲队1个月完成
总工程的_____,设乙队单独施工1个月能完成总
工程的 ,那么甲队半个月完成总工程的 __
,乙队半个月完成总工程的____,两队半个月完
成总工程的 .
分析:问题中的哪句话可以找等量关系从而列方程?
等量关系:甲完成的工作量+乙完成的工作量=1
例3 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
尝试根据等量关系列出方程
答:乙队的速度快。
根据题意得:
解:设乙队如果单独施工1个月能完成总工程的
方程两边同乘以 ,得:
解得:
检验: 时 , 是原方程的解。
由以上可知,若乙队单独工作一个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队施工速度快。
列分式方程应用题的步骤是什么?
1.审题;
2.设未知数;
3.列方程;
4.解方程;
5.检验(验两个方面);
6.作答。
1.甲、乙二人座某种机械零件.已知甲每小时比乙多做6个,甲90个所用的时间与乙做60个所有的时间相等。求甲乙每小时各做零件多少个?
分析:设甲每小时做 个零件,则乙每小时做 个零件,由“甲90个所用的时间与乙做60个所有的时间相等”可知等量关系为:
甲做90个所用的时间= 乙做60个所用的时间
列方程为:
2.某工程队需要在规定日期内完成。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
分析:设工作总量为“1”,规定日期为 天,
则甲独做 可完成,两天完成总工程的 ;
乙独做 天可完成,根据题意可知乙一共
做 天,共完成 。
由“恰好按期完成”可知:甲完成的工程+乙完成的工程=1
列方程为:
1.工程问题基本量有:工作量、工作时间、工作效率,
基本关系:工作总量=工作时间×工效。
2.不知道工作量的设工作总量为“1”,
知道具体工作总量的一般用具体的量。
通过学习工程问题,你有什么想法?
说明:应用分式方程解决实际问题与一元一次方程解决实际问题的步骤基本相同,但要注意验根。
一验是否是原方程的解;
二验是否符合实际问题。
例4:从2004年5月起某列列车平均提速 千米/时。用相同的时间,列车提速前行驶 千米,提速后比提速前多行驶50千米,提速前列车的平均速度是多少?
分析:这里的字母 和 表示已知量,设提速前的平均速度为x千米/时,则提速前列车行驶s千米所用
时间为 小时,提速后列车的平均速度为 千
米/时,提速后列车行驶 千米所用 的时间为
小时。
分析:问题中的哪句话可以找等量关系从而列方程?
例4:从2004年5月起某列列车平均提速 千米/时。用相同的时间,列车提速前行驶 千米,提速后比提速前多行驶50千米,提速前列车的平均速度是多少?
尝试根据等量关系列出方程
等量关系:
提速前行驶 千米的时间=提速后行驶 千米的时间
根据题意,得:
解:设提速前这次列车的平均速度为 千米∕小时
方程两边同乘以 ,得
解得:
检验:由于 和 都是正数, 时,
,故原方程的解为 。
答:提速前列车的平均速度为 千米/小时。
八年级学生去距学校10km的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达。已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度。
分析:设骑车速度为 千米/分钟 ,则汽车速度为 千米/分钟由“他们同时到达”可知等量关系为:
骑车学生所用时间-20分钟= 乘坐汽车所用的时间
列方程为:
1.行程问题基本量有:路程、时间、时间,
基本关系:路程=速度×时间。
2. 抓关键字句,从三个基本量找等量关系。
3.工程问题和行程问题有相似之处,分析问题时两者可类比,
借助表格和线段图进行。
通过对行程问题的学习,你有什么想法?
补充:应用分式方程解决实际问题要注意验根;在具体问题中可设参数充当已知量;注意单位的统一。
(1)工程问题基本关系… …
(2)行程问题基本关系… …
(3)列分式方程解应用题的步骤是什么?关键是什么?
(4)列整式方程解应用题的过程有什么区别和联系?
本节课我学习了… …
2(拓展)、 请根据下面的分式方程设计实际生活情境的应用题,并解答。
1、作业:教材154页3——6.
——分式方程解应用题
解分式方程
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a
最简公分母是
否为零?
注意验根哦
步骤
列一元一次方程解应用题的步骤是什么?
1.审题;
2.设未知数;
3.列方程;
4.解方程;
5.作答。
1、(1)工程问题基本公式:
(2)某项工程甲独做10天完成,则每天完成
,乙独做6天完成这项工程的 ,则
需 天完成 ,每天完成 。
工作量=工时×工效,
(3)某公司需要600台机器,甲工厂12天可完成,则甲工厂每天生产 台,乙工厂每天比甲多生产10台,则乙工厂 天可以完成。
50
10
此时,不知具体的工作总量,常常设为“1”。
此时,知道工作总量是600台,在解决问题时常用具体的工作量。
2、(1)行程问题基本公式:路程=速度×时间,
常用字母:路程——S,速度——V,时间——t
(2)某汽车从甲地开往乙地,每小时行驶50千米,6小时可以到达,如果要提前1小时到达,则每小时行驶 千米。
60
例3 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
分析:常常设工作总量为“1”,甲队1个月完成
总工程的_____,设乙队单独施工1个月能完成总
工程的 ,那么甲队半个月完成总工程的 __
,乙队半个月完成总工程的____,两队半个月完
成总工程的 .
分析:问题中的哪句话可以找等量关系从而列方程?
等量关系:甲完成的工作量+乙完成的工作量=1
例3 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
尝试根据等量关系列出方程
答:乙队的速度快。
根据题意得:
解:设乙队如果单独施工1个月能完成总工程的
方程两边同乘以 ,得:
解得:
检验: 时 , 是原方程的解。
由以上可知,若乙队单独工作一个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队施工速度快。
列分式方程应用题的步骤是什么?
1.审题;
2.设未知数;
3.列方程;
4.解方程;
5.检验(验两个方面);
6.作答。
1.甲、乙二人座某种机械零件.已知甲每小时比乙多做6个,甲90个所用的时间与乙做60个所有的时间相等。求甲乙每小时各做零件多少个?
分析:设甲每小时做 个零件,则乙每小时做 个零件,由“甲90个所用的时间与乙做60个所有的时间相等”可知等量关系为:
甲做90个所用的时间= 乙做60个所用的时间
列方程为:
2.某工程队需要在规定日期内完成。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
分析:设工作总量为“1”,规定日期为 天,
则甲独做 可完成,两天完成总工程的 ;
乙独做 天可完成,根据题意可知乙一共
做 天,共完成 。
由“恰好按期完成”可知:甲完成的工程+乙完成的工程=1
列方程为:
1.工程问题基本量有:工作量、工作时间、工作效率,
基本关系:工作总量=工作时间×工效。
2.不知道工作量的设工作总量为“1”,
知道具体工作总量的一般用具体的量。
通过学习工程问题,你有什么想法?
说明:应用分式方程解决实际问题与一元一次方程解决实际问题的步骤基本相同,但要注意验根。
一验是否是原方程的解;
二验是否符合实际问题。
例4:从2004年5月起某列列车平均提速 千米/时。用相同的时间,列车提速前行驶 千米,提速后比提速前多行驶50千米,提速前列车的平均速度是多少?
分析:这里的字母 和 表示已知量,设提速前的平均速度为x千米/时,则提速前列车行驶s千米所用
时间为 小时,提速后列车的平均速度为 千
米/时,提速后列车行驶 千米所用 的时间为
小时。
分析:问题中的哪句话可以找等量关系从而列方程?
例4:从2004年5月起某列列车平均提速 千米/时。用相同的时间,列车提速前行驶 千米,提速后比提速前多行驶50千米,提速前列车的平均速度是多少?
尝试根据等量关系列出方程
等量关系:
提速前行驶 千米的时间=提速后行驶 千米的时间
根据题意,得:
解:设提速前这次列车的平均速度为 千米∕小时
方程两边同乘以 ,得
解得:
检验:由于 和 都是正数, 时,
,故原方程的解为 。
答:提速前列车的平均速度为 千米/小时。
八年级学生去距学校10km的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达。已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度。
分析:设骑车速度为 千米/分钟 ,则汽车速度为 千米/分钟由“他们同时到达”可知等量关系为:
骑车学生所用时间-20分钟= 乘坐汽车所用的时间
列方程为:
1.行程问题基本量有:路程、时间、时间,
基本关系:路程=速度×时间。
2. 抓关键字句,从三个基本量找等量关系。
3.工程问题和行程问题有相似之处,分析问题时两者可类比,
借助表格和线段图进行。
通过对行程问题的学习,你有什么想法?
补充:应用分式方程解决实际问题要注意验根;在具体问题中可设参数充当已知量;注意单位的统一。
(1)工程问题基本关系… …
(2)行程问题基本关系… …
(3)列分式方程解应用题的步骤是什么?关键是什么?
(4)列整式方程解应用题的过程有什么区别和联系?
本节课我学习了… …
2(拓展)、 请根据下面的分式方程设计实际生活情境的应用题,并解答。
1、作业:教材154页3——6.
