人教版数学八年级上册课件:11.1.1三角形的边(25张)
文档属性
| 名称 | 人教版数学八年级上册课件:11.1.1三角形的边(25张) |  | |
| 格式 | ppt | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 08:04:41 | ||
图片预览








文档简介
*
观察思考:以下的图中,都出现了什么几何图形?如何去定义这种几何图形?
*
*
*
*
电线杆
自行车
11.1.1三角形的边
Page ? *
掌握三角形的表示方法及其分类,会用三角形的三边关系解决一些实际问题
*
1、三角形的定义
请同学们阅读P2的内容,把下面的内容补充完整:
3、三角形的表示
三角形用符号“ ”表示,顶点是A,B,C的三角形,记作“△ABC”(一定要用大写字母表示)读作“ ”。记三角形时,顶点字母一般按字母表中的顺序排列。
2、三角形的顶点、边、角
如右图所示,组成三角形的三条线段叫做三角形的边,分别是:线段 ;三角形相邻两边的公共端点(点 )叫做三角形的顶点; 是相邻两边组成的角,叫做三角形的内角,简称 。
三角形的三边有时用它所对角的小写字母来表示,如∠A所对的边是BC或a ,那么∠B所对的边是 或 ,边a所对的角是 。
由不在 的三条线段 所组成的图形,叫做三角形。
A
B
C
c
a
b
4、对边与对角的关系:
同一直线上
首尾顺次相接
AB,BC,CA
A,B,C
ㄥA,ㄥB,ㄥC
三角形的角
△
三角形ABC
AC
b
∠A
*
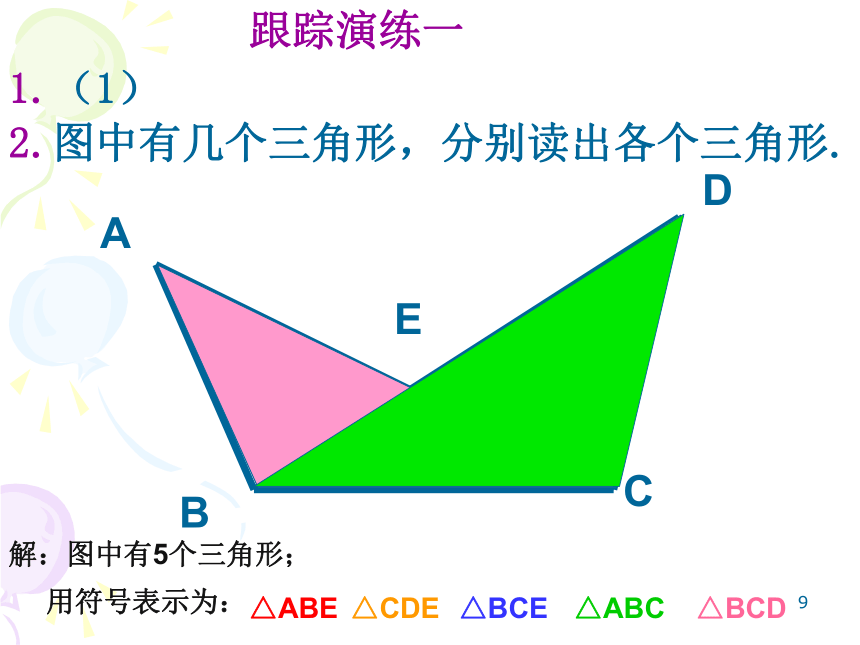
2.图中有几个三角形,分别读出各个三角形.
A
D
B
E
C
△ABE
△CDE
△BCE
△ABC
△BCD
解:图中有5个三角形;
用符号表示为:
1.(1)
跟踪演练一
*
思考
小学时我们就已经学习了三角形的相关知识,对三角形有了初步的认识。那么,回想一下,三角形按边可以分成哪几类?按角分呢?
请同学们从P2页的最后一段开始阅读,到P3页的第5段为止,完成下面的内容:
*
:有一个角是 ;
:有一个角大于 。
:有两条边相等;
:有 条边相等;
在等腰三角形中,相等的两边都叫做 ,
另一边叫做 ,两腰的夹角叫做 ,腰和
底边的夹角叫 。
A
B
C
腰
腰
底角
底角
顶角
底
直角三角形
钝角三角形
900
900
三
腰
底边
顶角
底角
*
1、判断,对的打“√”,错的打“×”.
(1)所有的等边三角形都是等腰三角形. ( )
(2)等腰三角形一定是锐角三角形. ( )
(3)有一个角大于90°的三角形是钝角三角形. ( )
(4)三角形按边的长短关系可分为等边三角形和不等边三角形.
( )
2、由3cm,3cm,5cm长围成的三角形是_____三角形,腰是____,底是____,等腰三角形有____条腰.
3、如图,等腰三角形ABC的顶角为_____度,底角为_____度.
√
√
×
×
等腰
3cm
5cm
2
40
70
*
探究4:
蚂蚁要从B点去C点觅食,请你帮忙选择最佳的路径。
B
C
A
1.从B到C有几条路?
两条。
2.哪条路最近?为什么?
BC
AB
+
AC
>
BC,两点之间线段最短。
BC
AB
+
>
AC
BC
AC
+
>
AB
能用简练的语言说一说这三边的关系吗?
小结:
三角形中,任意两边之和大于第三边。
这三个式子同时存在
问题:
*
B
A
C
动手试一试:如何填下列空?
小结:
三角形中,任意两边之差小于第三边。
AC
BC
AB
BC
AB
-
<
AC
AC
-
AB
BC
-
<
<
能用简练的语言说一说三边之间的关系吗?
(1)
(2)
(3)
这三个式子同时存在
*
归纳
三角形三边关系定理:三角形两边的和大于第三边。
A
B
C
c
a
b
如:BC+AC>AB
a+b>c
三角形三边关系定理:三角形两边的差小于第三边。
如:BC-ACa-ba - b < c < a + b
三角形的第三边小于两边的和
而大于两边的差。
*
例1:已知三条线段的长分别为5、9、12,这三条线段能否构成三角形呢?
∵5+9>12
5+12>9
9+12>5
解:
∴这三条线段能构成三角形。
判断过程能否更简单一点呢?
较小两条线段的和>最长线段
则这三条线段可以构成三角形。
*
下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
*
不能
不能
能
3
C
*
用一条长为18cm的细绳围成一个等腰三角形:
(1)如果腰长是5cm,那么各边的长是多少?
(2)如果腰长是底边的2倍,那么各边长是多少?
(3)能围成底边长是4cm的等腰三角形吗?为什么?
(4)能围成腰长是4cm的等腰三角形吗?为什么?
A
B
C
例2:
(1)5cm,5cm, 8cm。
(2)3.6cm,7.2cm, 7.2cm。
(4)不能,因为4+4<10,不符合
三角形两边的和大于第三边,所以不能。
(3)能,因为4+7>7,符合
三角形两边的和大于第三边,所以能。
*
(二).阅读课本3页例题,
仿照例题解法完成下面这个问题:
仿例:一个三角形有两条边相等,周长为20cm,
三角形的一边长6cm,求其他两边长。
解:当底边为6cm时,设腰长为xcm,则:
6+x+x=20
当腰长为6cm时,设底边为xcm,则:
解得:x=7
6+x+x=20
所以当底边为6cm时,其他两边长分别为7cm, 7cm。
解得:x=8
所以当腰长为6cm时,其他两边长分别为6cm, 8cm。
*
能力提升:
在△ABC中,若a =3,b=7,则第
三边c的取值范围是 。
既要考虑“两边的和大于第三边”,
又要考虑“两边的差小于第三边”
a - b < c < a + b
在△ABC中,若a =3,b=7,则其周
长l的取值范围是 。
4 < c < 10
14 < l< 20
*
C
15cm,20cm, 25cm。
5或4
2
*
1、请用所学的数学知识解释:
2.两点之间的所有连线中,线段最短
1.三角形任意两边之和大于第三边
人行横道
.A
.B
为什么经常有行人斜穿马路而不走人行横道?
实际运用:
Page ? *
忆一忆:
今天我们学了哪些内容?
1.三角形的有关概念(边、角、顶点)
2.会用符号表示一个三角形.
3.通过实践了解三角形的三边不等关系.
a - b < c < a + b
*
P8习题11.1
第1、2题.
作业:
观察思考:以下的图中,都出现了什么几何图形?如何去定义这种几何图形?
*
*
*
*
电线杆
自行车
11.1.1三角形的边
Page ? *
掌握三角形的表示方法及其分类,会用三角形的三边关系解决一些实际问题
*
1、三角形的定义
请同学们阅读P2的内容,把下面的内容补充完整:
3、三角形的表示
三角形用符号“ ”表示,顶点是A,B,C的三角形,记作“△ABC”(一定要用大写字母表示)读作“ ”。记三角形时,顶点字母一般按字母表中的顺序排列。
2、三角形的顶点、边、角
如右图所示,组成三角形的三条线段叫做三角形的边,分别是:线段 ;三角形相邻两边的公共端点(点 )叫做三角形的顶点; 是相邻两边组成的角,叫做三角形的内角,简称 。
三角形的三边有时用它所对角的小写字母来表示,如∠A所对的边是BC或a ,那么∠B所对的边是 或 ,边a所对的角是 。
由不在 的三条线段 所组成的图形,叫做三角形。
A
B
C
c
a
b
4、对边与对角的关系:
同一直线上
首尾顺次相接
AB,BC,CA
A,B,C
ㄥA,ㄥB,ㄥC
三角形的角
△
三角形ABC
AC
b
∠A
*
2.图中有几个三角形,分别读出各个三角形.
A
D
B
E
C
△ABE
△CDE
△BCE
△ABC
△BCD
解:图中有5个三角形;
用符号表示为:
1.(1)
跟踪演练一
*
思考
小学时我们就已经学习了三角形的相关知识,对三角形有了初步的认识。那么,回想一下,三角形按边可以分成哪几类?按角分呢?
请同学们从P2页的最后一段开始阅读,到P3页的第5段为止,完成下面的内容:
*
:有一个角是 ;
:有一个角大于 。
:有两条边相等;
:有 条边相等;
在等腰三角形中,相等的两边都叫做 ,
另一边叫做 ,两腰的夹角叫做 ,腰和
底边的夹角叫 。
A
B
C
腰
腰
底角
底角
顶角
底
直角三角形
钝角三角形
900
900
三
腰
底边
顶角
底角
*
1、判断,对的打“√”,错的打“×”.
(1)所有的等边三角形都是等腰三角形. ( )
(2)等腰三角形一定是锐角三角形. ( )
(3)有一个角大于90°的三角形是钝角三角形. ( )
(4)三角形按边的长短关系可分为等边三角形和不等边三角形.
( )
2、由3cm,3cm,5cm长围成的三角形是_____三角形,腰是____,底是____,等腰三角形有____条腰.
3、如图,等腰三角形ABC的顶角为_____度,底角为_____度.
√
√
×
×
等腰
3cm
5cm
2
40
70
*
探究4:
蚂蚁要从B点去C点觅食,请你帮忙选择最佳的路径。
B
C
A
1.从B到C有几条路?
两条。
2.哪条路最近?为什么?
BC
AB
+
AC
>
BC,两点之间线段最短。
BC
AB
+
>
AC
BC
AC
+
>
AB
能用简练的语言说一说这三边的关系吗?
小结:
三角形中,任意两边之和大于第三边。
这三个式子同时存在
问题:
*
B
A
C
动手试一试:如何填下列空?
小结:
三角形中,任意两边之差小于第三边。
AC
BC
AB
BC
AB
-
<
AC
AC
-
AB
BC
-
<
<
能用简练的语言说一说三边之间的关系吗?
(1)
(2)
(3)
这三个式子同时存在
*
归纳
三角形三边关系定理:三角形两边的和大于第三边。
A
B
C
c
a
b
如:BC+AC>AB
a+b>c
三角形三边关系定理:三角形两边的差小于第三边。
如:BC-AC
三角形的第三边小于两边的和
而大于两边的差。
*
例1:已知三条线段的长分别为5、9、12,这三条线段能否构成三角形呢?
∵5+9>12
5+12>9
9+12>5
解:
∴这三条线段能构成三角形。
判断过程能否更简单一点呢?
较小两条线段的和>最长线段
则这三条线段可以构成三角形。
*
下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
*
不能
不能
能
3
C
*
用一条长为18cm的细绳围成一个等腰三角形:
(1)如果腰长是5cm,那么各边的长是多少?
(2)如果腰长是底边的2倍,那么各边长是多少?
(3)能围成底边长是4cm的等腰三角形吗?为什么?
(4)能围成腰长是4cm的等腰三角形吗?为什么?
A
B
C
例2:
(1)5cm,5cm, 8cm。
(2)3.6cm,7.2cm, 7.2cm。
(4)不能,因为4+4<10,不符合
三角形两边的和大于第三边,所以不能。
(3)能,因为4+7>7,符合
三角形两边的和大于第三边,所以能。
*
(二).阅读课本3页例题,
仿照例题解法完成下面这个问题:
仿例:一个三角形有两条边相等,周长为20cm,
三角形的一边长6cm,求其他两边长。
解:当底边为6cm时,设腰长为xcm,则:
6+x+x=20
当腰长为6cm时,设底边为xcm,则:
解得:x=7
6+x+x=20
所以当底边为6cm时,其他两边长分别为7cm, 7cm。
解得:x=8
所以当腰长为6cm时,其他两边长分别为6cm, 8cm。
*
能力提升:
在△ABC中,若a =3,b=7,则第
三边c的取值范围是 。
既要考虑“两边的和大于第三边”,
又要考虑“两边的差小于第三边”
a - b < c < a + b
在△ABC中,若a =3,b=7,则其周
长l的取值范围是 。
4 < c < 10
14 < l< 20
*
C
15cm,20cm, 25cm。
5或4
2
*
1、请用所学的数学知识解释:
2.两点之间的所有连线中,线段最短
1.三角形任意两边之和大于第三边
人行横道
.A
.B
为什么经常有行人斜穿马路而不走人行横道?
实际运用:
Page ? *
忆一忆:
今天我们学了哪些内容?
1.三角形的有关概念(边、角、顶点)
2.会用符号表示一个三角形.
3.通过实践了解三角形的三边不等关系.
a - b < c < a + b
*
P8习题11.1
第1、2题.
作业:
