人教版数学八年级下册课件: 18.1.1平行四边形的性质(26张)
文档属性
| 名称 | 人教版数学八年级下册课件: 18.1.1平行四边形的性质(26张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 951.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览




文档简介
平行四边形
活动一:认识平行四边形
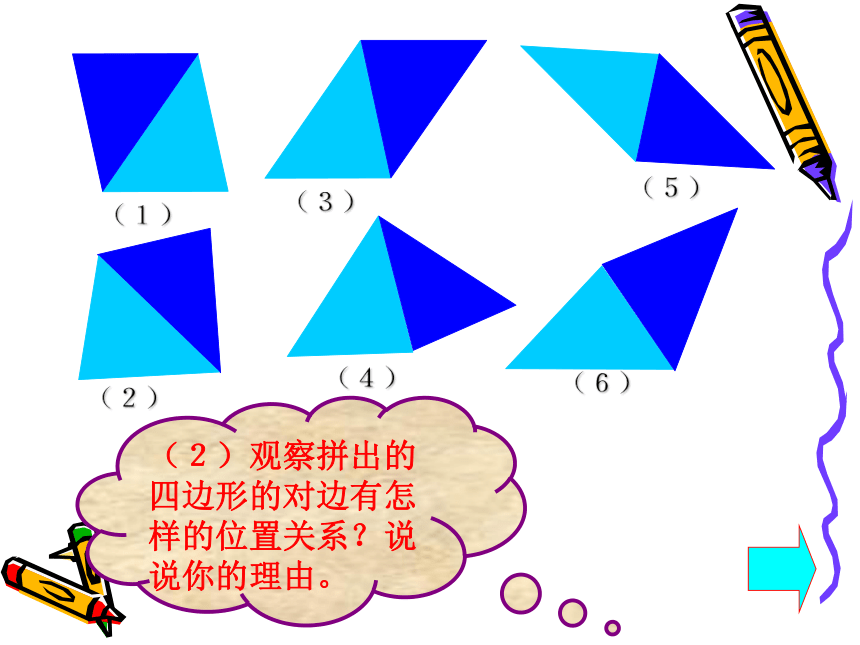
( 1)你能用手中的两张全等的三角形纸板在平面内拼出四边形吗?
(1)
(3)
(2)
(4)
(5)
(6)
(2)观察拼出的四边形的对边有怎样的位置关系?说说你的理由。
探究要求:
(1)小组合作探究 ;
(2)使用相关学具(全等的三角形纸板、平行四边形纸板各一对,圆规、刻度尺,量角器,图钉);
(3)采用度量、平移、旋转、折叠等方法。
活动二:探索平行四边形的性质
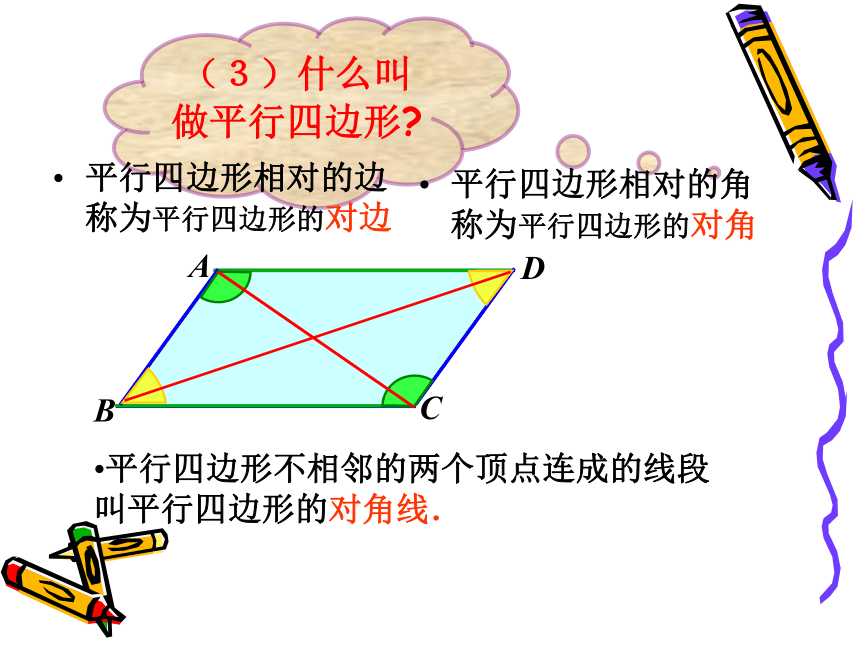
(3)什么叫做平行四边形?
A
D
B
C
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
平行四边形相对的边称为平行四边形的对边
平行四边形相对的角称为平行四边形的对角
F
1
2
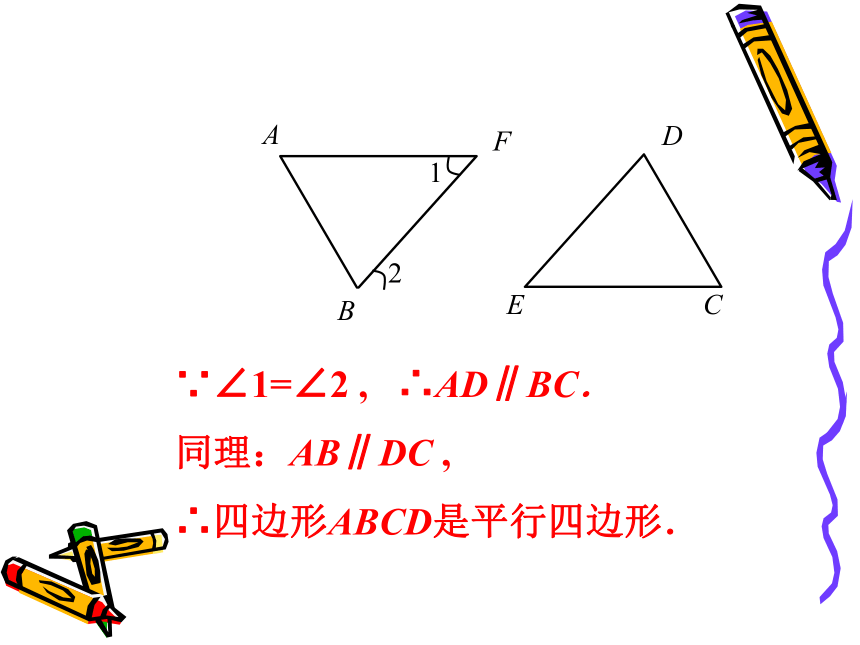
∵∠1=∠2 , ∴AD∥BC.
同理:AB∥DC ,
∴四边形ABCD是平行四边形.
D
E
C
A
B
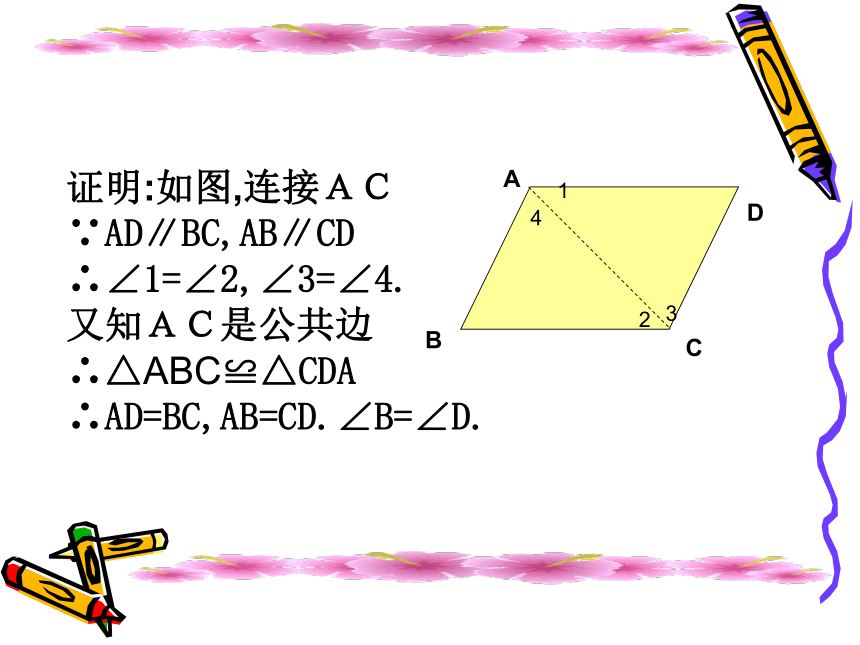
证明:如图,连接AC∵AD∥BC,AB∥CD
∴∠1=∠2,∠3=∠4.
又知AC是公共边
∴△ABC≌△CDA
∴AD=BC,AB=CD.∠B=∠D.
A
C
B
D
1
3
2
4
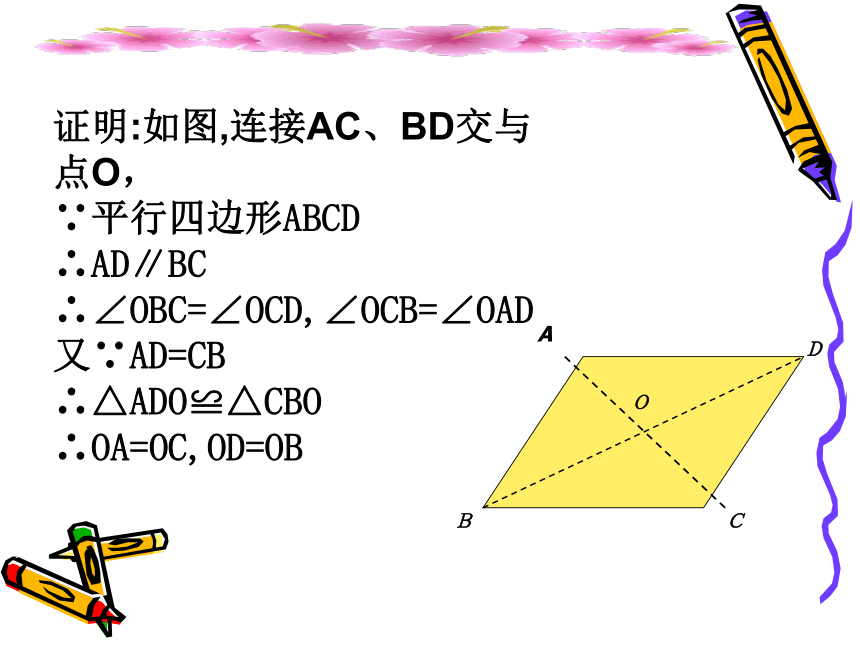
证明:如图,连接AC、BD交与点O,
∵平行四边形ABCD
∴AD∥BC
∴∠OBC=∠OCD,∠OCB=∠OAD
又∵AD=CB
∴△ADO≌△CBO
∴OA=OC,OD=OB
A
B
C
D
O
O
A
B
C
D
(C)
(A)
(B)
(D)
将 ABCD绕点O旋转1800观察它和
原平行四边形重合
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的性质
A
B
C
D
平行四边形对角线互相平分.
汇报成果:
O
平行四边形的性质
1.平行四边形的对边相等.
2.平行四边形的对角相等.
3.平行四边形的对角线互相平分.
论证:
小红量得地面上的平行四边形的影子的一个内角是30°,就说知道了其余三个内角的度数,又用刻度尺量出一组邻边的长分别是140cm和255cm,便胸有成竹的说能够计算出这个平行四边形的周长和面积.你知道小红如何计算的吗?
30°
140cm
255cm
D
∟
A
C
B
E
解:∵四边形ABCD是平行四边形
∴∠A=∠C, ∠B=∠D, ∠A+∠B=180°
又∵∠A=30 °
∴ ∠C=30 ° ∠B=∠D=180°-30°=150°
过点D作DE⊥BC于E,则∠DEC=90°
∵ ∠C=30 °∴DE=0.5CD=0.5×140=70cm
∴平行四边形ABCD的面积=255×70=17850c㎡
255cm
140cm
30°
∵四边形ABCD是平行四边形
∴AB=CD=140cm,AD=BC=255cm
∴平行四边形ABCD的周长=2×(140+255)=790cm
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
探索创造未来
数学成就梦想
在数学的天地里,重要的不仅是我们知道什么,更重要的是我们应该怎么知道什么。
——毕达哥拉斯
(一)填一填,看谁做的快
如图所示,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝
BC= ㎝;。
2)若∠A=70°,则∠B= 。
∠C= 。
3)若∠A+∠C=80°,
则∠A= ; ∠D=
4)若∠A﹕∠B=1﹕2,则各角的度数为
6
9
110°
70°
40°
140°
A
B
C
D
60°120°60°120°
活动三:开放训练 实践应用
(二)解疑:某时刻小红量得地面上的平行四边形的影子的一个内角是30°,就说知道了其余三个内角的度数,又用直尺量出一组邻边的长分别是40cm和55cm,便胸有成竹的说能够计算出这个平行四边形的周长和面积.你知道小红如何计算的吗?这样计算的根据是什么?
(三)探究:用图钉把一根平放在平行四边形ABCD上的细纸板条固定在对角线AC、BD的 交点O处,拨动纸板条,使它随意的停留在任意的位置。观察几次拨动的结果,你有什么新发现?你能验证自己的发现吗?观察
A
B
C
D
E
F
O
平行四边形的性质
∵四边形ABCD是平行四边形,
∴AB=CD , AD=BC.
∵四边形ABCD是平行四边形,
∴∠BAD=∠DCB , ∠ABC=∠CDA.
∵四边形ABCD是平行四边形,
∴AO=CO , BO=DO.
A
D
B
C
O
符号表示
ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系,并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
探究
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
变一变
●
●
●
●
在上述问题中,若将直线EF绕点O旋转至下
图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
●
●
●
●
再变一变
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
学过了本节课,你有哪些收获?
1.平行四边形的定义、表示方法
2.平行四边形的性质:
平行四边形的对边平行
平行四边形的对边相等
平行四边形的对角相等(邻角互补)
平行四边形的对角线互相平分
3.不仅可以用测量、拼图、旋转等方法,还可以用证明的方法来探索平行四边形的性质。
活动四:自我总结 收获快乐
1.必做:教材43页第1、2题,44页第1、2题
2.选做:教材49页第3题,
3.探究:已知任意三点A、B、C是否存在点D使A、B、C、D围成一个平行四边形,如果存在请你作出,如不存在,请说明理由。
活动五:作业布置 课后延展
活动一:认识平行四边形
( 1)你能用手中的两张全等的三角形纸板在平面内拼出四边形吗?
(1)
(3)
(2)
(4)
(5)
(6)
(2)观察拼出的四边形的对边有怎样的位置关系?说说你的理由。
探究要求:
(1)小组合作探究 ;
(2)使用相关学具(全等的三角形纸板、平行四边形纸板各一对,圆规、刻度尺,量角器,图钉);
(3)采用度量、平移、旋转、折叠等方法。
活动二:探索平行四边形的性质
(3)什么叫做平行四边形?
A
D
B
C
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
平行四边形相对的边称为平行四边形的对边
平行四边形相对的角称为平行四边形的对角
F
1
2
∵∠1=∠2 , ∴AD∥BC.
同理:AB∥DC ,
∴四边形ABCD是平行四边形.
D
E
C
A
B
证明:如图,连接AC∵AD∥BC,AB∥CD
∴∠1=∠2,∠3=∠4.
又知AC是公共边
∴△ABC≌△CDA
∴AD=BC,AB=CD.∠B=∠D.
A
C
B
D
1
3
2
4
证明:如图,连接AC、BD交与点O,
∵平行四边形ABCD
∴AD∥BC
∴∠OBC=∠OCD,∠OCB=∠OAD
又∵AD=CB
∴△ADO≌△CBO
∴OA=OC,OD=OB
A
B
C
D
O
O
A
B
C
D
(C)
(A)
(B)
(D)
将 ABCD绕点O旋转1800观察它和
原平行四边形重合
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的性质
A
B
C
D
平行四边形对角线互相平分.
汇报成果:
O
平行四边形的性质
1.平行四边形的对边相等.
2.平行四边形的对角相等.
3.平行四边形的对角线互相平分.
论证:
小红量得地面上的平行四边形的影子的一个内角是30°,就说知道了其余三个内角的度数,又用刻度尺量出一组邻边的长分别是140cm和255cm,便胸有成竹的说能够计算出这个平行四边形的周长和面积.你知道小红如何计算的吗?
30°
140cm
255cm
D
∟
A
C
B
E
解:∵四边形ABCD是平行四边形
∴∠A=∠C, ∠B=∠D, ∠A+∠B=180°
又∵∠A=30 °
∴ ∠C=30 ° ∠B=∠D=180°-30°=150°
过点D作DE⊥BC于E,则∠DEC=90°
∵ ∠C=30 °∴DE=0.5CD=0.5×140=70cm
∴平行四边形ABCD的面积=255×70=17850c㎡
255cm
140cm
30°
∵四边形ABCD是平行四边形
∴AB=CD=140cm,AD=BC=255cm
∴平行四边形ABCD的周长=2×(140+255)=790cm
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
探索创造未来
数学成就梦想
在数学的天地里,重要的不仅是我们知道什么,更重要的是我们应该怎么知道什么。
——毕达哥拉斯
(一)填一填,看谁做的快
如图所示,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝
BC= ㎝;。
2)若∠A=70°,则∠B= 。
∠C= 。
3)若∠A+∠C=80°,
则∠A= ; ∠D=
4)若∠A﹕∠B=1﹕2,则各角的度数为
6
9
110°
70°
40°
140°
A
B
C
D
60°120°60°120°
活动三:开放训练 实践应用
(二)解疑:某时刻小红量得地面上的平行四边形的影子的一个内角是30°,就说知道了其余三个内角的度数,又用直尺量出一组邻边的长分别是40cm和55cm,便胸有成竹的说能够计算出这个平行四边形的周长和面积.你知道小红如何计算的吗?这样计算的根据是什么?
(三)探究:用图钉把一根平放在平行四边形ABCD上的细纸板条固定在对角线AC、BD的 交点O处,拨动纸板条,使它随意的停留在任意的位置。观察几次拨动的结果,你有什么新发现?你能验证自己的发现吗?观察
A
B
C
D
E
F
O
平行四边形的性质
∵四边形ABCD是平行四边形,
∴AB=CD , AD=BC.
∵四边形ABCD是平行四边形,
∴∠BAD=∠DCB , ∠ABC=∠CDA.
∵四边形ABCD是平行四边形,
∴AO=CO , BO=DO.
A
D
B
C
O
符号表示
ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系,并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
探究
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
变一变
●
●
●
●
在上述问题中,若将直线EF绕点O旋转至下
图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
●
●
●
●
再变一变
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
学过了本节课,你有哪些收获?
1.平行四边形的定义、表示方法
2.平行四边形的性质:
平行四边形的对边平行
平行四边形的对边相等
平行四边形的对角相等(邻角互补)
平行四边形的对角线互相平分
3.不仅可以用测量、拼图、旋转等方法,还可以用证明的方法来探索平行四边形的性质。
活动四:自我总结 收获快乐
1.必做:教材43页第1、2题,44页第1、2题
2.选做:教材49页第3题,
3.探究:已知任意三点A、B、C是否存在点D使A、B、C、D围成一个平行四边形,如果存在请你作出,如不存在,请说明理由。
活动五:作业布置 课后延展
