人教版数学九年级上册 22.1.4 二次函数 y=ax2+bx+c 的图象和性质 课件(共34张PPT)
文档属性
| 名称 | 人教版数学九年级上册 22.1.4 二次函数 y=ax2+bx+c 的图象和性质 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 23:52:45 | ||
图片预览










文档简介
第二十二章 二次函数
人教版数学九年级上册
22.1.4 二次函数 y=ax2+bx+c 的图象和性质
学习目标
1.会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.
2.会熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.
导入新知
火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以近似用h=-5t2+150t+10表示.那么经过多长时间,火箭达到它的最高点?
我们已经知道 y=a(x-h)2+k 的图象和性质,能否利用这些知识来讨论 的图象和性质?
合作探究
配方可得
怎样将 化成 y=a(x-h)2+k 的形式?
你能说出 的对称轴及顶点坐标吗?
对称轴是直线 x=6,顶点坐标是(6,3).
二次函数 可以看作是由 怎样平移得到的?
平移方法 1:
先向上平移 3 个单位,再向右平移 6 个单位得到的;
平移方法 2:
先向右平移 6 个单位,再向上平移 3 个单位得到的.
1.描点法:
①用配方法把二次函数 y=ax2+bx+c 化成 y=a(x-h)2+k 的形式;
②确定抛物线的开口方向、对称轴和顶点坐标,在对称轴两侧对称取点,按列表、描点、连线的步骤画出抛物线.
画二次函数 y=ax2+bx+c 的图象的方法
画二次函数 y=ax2+bx+c 的图象的方法
2.平移法
①用配方法把二次函数 y=ax2+bx+c 化成 y=a(x-h)2+k 的形式,明确顶点 (h,k);
②作出抛物线 y=ax2;
③将抛物线 y=ax2 平移,使其顶点平移到 (h,k) 处.
…
…
…
…
9
8
7
6
5
4
3
x
先利用图形的对称性列表.
7.5
5
3.5
3
3.5
5
7.5
?
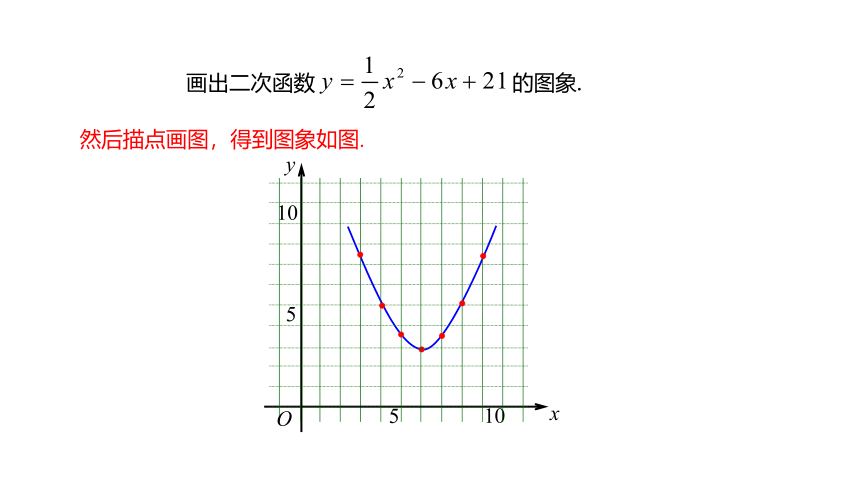
画出二次函数 的图象.
5
10
x
y
5
10
然后描点画图,得到图象如图.
O
画出二次函数 的图象.
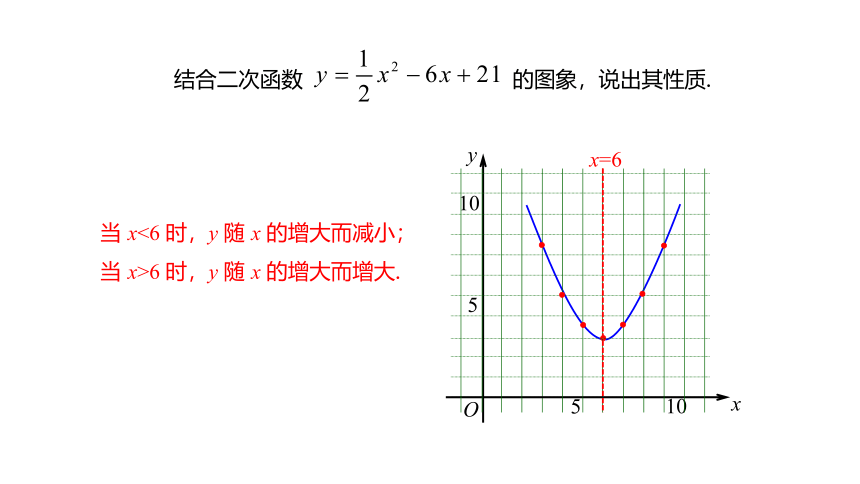
结合二次函数 的图象,说出其性质.
5
10
x
y
5
10
x=6
当 x<6 时,y 随 x 的增大而减小;
当 x>6 时,y 随 x 的增大而增大.
O
?
?
?
?
?
典型例题
我们如何用配方法将一般式 y=ax2+bx+c(a≠0) 化成顶点式 y=a(x-h)2+k?
合作探究
y=ax?+bx+c
一般地,二次函数 y=ax2+bx+c 可以通过配方法化成 y=a(x-h)2+k 的形式,即
因此,抛物线 y=ax2+bx+c 的顶点坐标是:
对称轴是:
直线
x
y
O
如果 a>0,
当 x< 时,y 随 x 的增大而减小;
当 x> 时,y 随 x 的增大而增大.
x
y
O
如果 a<0,
当 x< 时,y 随 x 的增大而增大;
当 x> 时,y 随 x 的增大而减小.
已知二次函数 y=-2x2+4x+3,请回答下列问题:
(1)试确定该函数图象的开口方向、对称轴和顶点坐标;
(2)在平面直角坐标系中,画出二次函数 y=-2x2+4x+3 的图象,并指出抛物线 y=-2x2+4x+3 是由抛物线y=-2x2 经过怎样的平移得到的;
(3)对于二次函数 y=-2x2+4x+3,当 x 取何值时,y 随 x 的增大而减小?
判断抛物线 y=ax2 经过怎样的平移能得到抛物线 y=ax2+bx+c 时,通常先将 y=ax2+bx+c 配成y=a(x-h)2+k 的形式,再根据“左加右减自变量,上加下减常数项”判断平移方式,或者根据顶点的位置确定平移方式.
典型例题
技巧
x
y
O
二次函数 的图象如下图所示,请根据二次函数的性质填空:
a1 ___ 0
b1___ 0
c1___ 0
a2___ 0
b2___ 0
c2___ 0
>
>
>
>
<
=
开口向上,a>0
对称轴在y轴左侧,
对称轴在y轴右侧,
x=0时,y=c.
合作探究
x
y
O
a3___ 0
b3___ 0
c3___ 0
a4___ 0
b4___ 0
c4___ 0
<
=
>
<
>
<
开口向下,a<0
?
?
x=0时,y=c.
二次函数 y=ax2+bx+c 的图象与 a,b,c 的关系
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}字母符号
图象的特征
a>0
开口__________
a<0
开口__________
b=0
对称轴为_____轴
a,b同号
对称轴在y轴的____侧
a,b异号
对称轴在y轴的____侧
c=0
经过原点
c>0
与y轴交于_____半轴
c<0
与y轴交于_____半轴
向上
向下
y
左
右
正
负
二次函数 y=ax2+bx+c 中,a 的符号决定抛物线的开口方向,a,b 的符号决定抛物线的对称轴的大致位置,c 的符号决定抛物线与 y 轴交点的大致位置.
二次函数 y=ax2+bx+c 的图象特征与系数 a,b,c 的符号之间的关系是互逆的,即由字母的符号能确定图象的特征,反之,根据图象的特征,也可以确定其解析式 y=ax2+bx+c 中系数 a,b,c的符号.
A.1 B.2 C.3 D.4
二次函数 y=ax2+bx+c 的图象如图所示,给出下列结论:①b<0;②c>0;③a+b+c>0;④4a+2b+c<0.其中正确的个数是( )
C
解:①因为二次函数 y=ax2+bx+c 的图象的开口方向是向下,所以 a<0,
根据对称轴在 y 轴的右侧,所以a,b的符号相反,得出b>0,故①错误;
②因为二次函数 y=ax2+bx+c的图象与y轴正半轴相交,所以c>0,故②正确;
③根据图象知,当x=1时,y>0,即a+b+c>0,故③正确;
④根据图象知,当x=2时,y < 0,∴4a+2b+c<0,故④正确;
综上所述,正确结论共3个,故选C.
典型例题
1.若A(-4,y1),B(-3,y2),C(3,y3)为二次函数 y=x2+2x-6 的图象上的三点,则y1,y2,y3的大小关系是( )
B
A. y1解:因为A(-4,y1),B(-3,y2),C(3,y3)为二次函数y=x2+2x-6的图象上的三点,
y2=9-6-6=-3,即 y2=-3,
y3=9+6-6=9,即 y3=9,
因为-3<2<9,所以y2<y1<y3.
所以 y1=16-8-6=2,即 y1=2,
课堂练习
比较二次函数值大小的方法:
(1)代入比较法:若已知二次函数的解析式,可将几个点的横坐标分别代入二次函数的解析式,求出对应的函数值,再比较函数值的大小;
(2)增减性比较法:当点都在对称轴的同侧时,可直接根据函数的增减性比较大小,当点不在对称轴的同侧时,可利用二次函数图象的对称性,将点转化到对称轴的同侧,再利用增减性比较大小;
(3)根据点到对称轴的距离比较大小:当抛物线的开口向上时,点到对称轴的距离越大,相应的函数值越大,当抛物线的开口向下时,点到对称轴的距离越大,相应的函数值越小.
2.在平面直角坐标系中,把一条抛物线先向上平移 3 个单位长度,再作关于 x 轴对称的图象,得到抛物线 y=x2+5x+6,则原抛物线的解析式为( )
B
?
?
3.分别在下列范围内求函数 y=x2-2x-3 的最大值和最小值.
(1) -1≤x≤2; (2) 2≤x≤3.
解:因为 y=x2-2x-3=(x-1)2-4,
所以当 x<1 时,y 随 x 的增大而减小,
当 x>1 时,y 随 x 的增大而增大.
(1)由 -1≤x≤2 知,当 x=1时,y 有最小值 -4,
因为当 x=-1 时,y=0,当 x=2 时,y=-3,
所以当 x=-1 时,y 有最大值 0.
(2)当 2≤x≤3时,y 随 x 的增大而增大,
所以当 x=2 时,y 有最小值 -3,当 x=3 时,y 有最大值 0.
求二次函数的最值时,要先确定函数在自变量取值范围内的增减性,如果所给范围包含顶点的横坐标,则在顶点处取得最大(小)值;如果所给范围不包含顶点的横坐标,则利用函数的增减性确定最值.
A.图象与 y 轴的交点坐标为(0,1) B.图象的对称轴在 y 轴的右侧
C.当 x<0 时,y 随 x 的增大而减小 D. y 的最小值为 -3
1.关于二次函数 y=2x2+4x-1,下列说法正确的是( )
D
解:因为y=2x2+4x-1=2(x+1)2-3,
所以当x=0时,y=-1,故选项A错误,
该函数的对称轴是直线x=-1,故选项B错误,
当x<-1时,y随x的增大而减小,故选项C错误,
当x=-1时,y取得最小值,此时y=-3,故选项D正确.
中考实题
A. y3>y2>y1 B. y3>y1=y2 C. y1>y2>y3 D. y1=y2>y3
2.点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数 y=-x2+2x+c 的图象上,则y1,y2,y3 的大小关系是( )
D
解:因为 y=-x2+2x+c=-(x-1)2+1+c,
所以图象的开口向下,对称轴是直线x=1,
而P1(-1,y1)和P2(3,y2)到直线x=1的距离都为2,P3(5,y3)到直线x=1的距离为4,
所以y1=y2>y3.
故选D.
A.①②③ B.②③⑤ C.②③④ D.③④⑤
3.已知二次函数 y=ax2+bx+c(a≠0) 的图象如图所示,有下列 5 个结论:
①abc>0;②b-a>c;③4a+2b+c>0;④3a>-c;⑤a+b>m(am+b)(m≠1).
其中正确的结论有( )
解:①因为对称轴在y轴的右侧,所以ab<0,由图象可知c>0,
所以abc<0,故①不正确;
②当x=-1时,y=a-b+c<0,所以b-a>c,故②正确;
③由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0,故③正确;
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
(顶点式)
归纳新知
a>0
a<0
开口方向
顶点坐标
对称轴
增减性
最值
向上
向下
?
?
?
?
二次函数 y=ax2+bx+c 的图象与性质:
x=
?
A.①②③ B.②③⑤ C.②③④ D.③④⑤
已知二次函数 y=ax2+bx+c(a≠0) 的图象如图所示,有下列 5 个结论:
①abc>0;②b-a>c;③4a+2b+c>0;④3a>-c;⑤a+b>m(am+b)(m≠1).
其中正确的结论有( )
B
再 见
人教版数学九年级上册
22.1.4 二次函数 y=ax2+bx+c 的图象和性质
学习目标
1.会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.
2.会熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.
导入新知
火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以近似用h=-5t2+150t+10表示.那么经过多长时间,火箭达到它的最高点?
我们已经知道 y=a(x-h)2+k 的图象和性质,能否利用这些知识来讨论 的图象和性质?
合作探究
配方可得
怎样将 化成 y=a(x-h)2+k 的形式?
你能说出 的对称轴及顶点坐标吗?
对称轴是直线 x=6,顶点坐标是(6,3).
二次函数 可以看作是由 怎样平移得到的?
平移方法 1:
先向上平移 3 个单位,再向右平移 6 个单位得到的;
平移方法 2:
先向右平移 6 个单位,再向上平移 3 个单位得到的.
1.描点法:
①用配方法把二次函数 y=ax2+bx+c 化成 y=a(x-h)2+k 的形式;
②确定抛物线的开口方向、对称轴和顶点坐标,在对称轴两侧对称取点,按列表、描点、连线的步骤画出抛物线.
画二次函数 y=ax2+bx+c 的图象的方法
画二次函数 y=ax2+bx+c 的图象的方法
2.平移法
①用配方法把二次函数 y=ax2+bx+c 化成 y=a(x-h)2+k 的形式,明确顶点 (h,k);
②作出抛物线 y=ax2;
③将抛物线 y=ax2 平移,使其顶点平移到 (h,k) 处.
…
…
…
…
9
8
7
6
5
4
3
x
先利用图形的对称性列表.
7.5
5
3.5
3
3.5
5
7.5
?
画出二次函数 的图象.
5
10
x
y
5
10
然后描点画图,得到图象如图.
O
画出二次函数 的图象.
结合二次函数 的图象,说出其性质.
5
10
x
y
5
10
x=6
当 x<6 时,y 随 x 的增大而减小;
当 x>6 时,y 随 x 的增大而增大.
O
?
?
?
?
?
典型例题
我们如何用配方法将一般式 y=ax2+bx+c(a≠0) 化成顶点式 y=a(x-h)2+k?
合作探究
y=ax?+bx+c
一般地,二次函数 y=ax2+bx+c 可以通过配方法化成 y=a(x-h)2+k 的形式,即
因此,抛物线 y=ax2+bx+c 的顶点坐标是:
对称轴是:
直线
x
y
O
如果 a>0,
当 x< 时,y 随 x 的增大而减小;
当 x> 时,y 随 x 的增大而增大.
x
y
O
如果 a<0,
当 x< 时,y 随 x 的增大而增大;
当 x> 时,y 随 x 的增大而减小.
已知二次函数 y=-2x2+4x+3,请回答下列问题:
(1)试确定该函数图象的开口方向、对称轴和顶点坐标;
(2)在平面直角坐标系中,画出二次函数 y=-2x2+4x+3 的图象,并指出抛物线 y=-2x2+4x+3 是由抛物线y=-2x2 经过怎样的平移得到的;
(3)对于二次函数 y=-2x2+4x+3,当 x 取何值时,y 随 x 的增大而减小?
判断抛物线 y=ax2 经过怎样的平移能得到抛物线 y=ax2+bx+c 时,通常先将 y=ax2+bx+c 配成y=a(x-h)2+k 的形式,再根据“左加右减自变量,上加下减常数项”判断平移方式,或者根据顶点的位置确定平移方式.
典型例题
技巧
x
y
O
二次函数 的图象如下图所示,请根据二次函数的性质填空:
a1 ___ 0
b1___ 0
c1___ 0
a2___ 0
b2___ 0
c2___ 0
>
>
>
>
<
=
开口向上,a>0
对称轴在y轴左侧,
对称轴在y轴右侧,
x=0时,y=c.
合作探究
x
y
O
a3___ 0
b3___ 0
c3___ 0
a4___ 0
b4___ 0
c4___ 0
<
=
>
<
>
<
开口向下,a<0
?
?
x=0时,y=c.
二次函数 y=ax2+bx+c 的图象与 a,b,c 的关系
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}字母符号
图象的特征
a>0
开口__________
a<0
开口__________
b=0
对称轴为_____轴
a,b同号
对称轴在y轴的____侧
a,b异号
对称轴在y轴的____侧
c=0
经过原点
c>0
与y轴交于_____半轴
c<0
与y轴交于_____半轴
向上
向下
y
左
右
正
负
二次函数 y=ax2+bx+c 中,a 的符号决定抛物线的开口方向,a,b 的符号决定抛物线的对称轴的大致位置,c 的符号决定抛物线与 y 轴交点的大致位置.
二次函数 y=ax2+bx+c 的图象特征与系数 a,b,c 的符号之间的关系是互逆的,即由字母的符号能确定图象的特征,反之,根据图象的特征,也可以确定其解析式 y=ax2+bx+c 中系数 a,b,c的符号.
A.1 B.2 C.3 D.4
二次函数 y=ax2+bx+c 的图象如图所示,给出下列结论:①b<0;②c>0;③a+b+c>0;④4a+2b+c<0.其中正确的个数是( )
C
解:①因为二次函数 y=ax2+bx+c 的图象的开口方向是向下,所以 a<0,
根据对称轴在 y 轴的右侧,所以a,b的符号相反,得出b>0,故①错误;
②因为二次函数 y=ax2+bx+c的图象与y轴正半轴相交,所以c>0,故②正确;
③根据图象知,当x=1时,y>0,即a+b+c>0,故③正确;
④根据图象知,当x=2时,y < 0,∴4a+2b+c<0,故④正确;
综上所述,正确结论共3个,故选C.
典型例题
1.若A(-4,y1),B(-3,y2),C(3,y3)为二次函数 y=x2+2x-6 的图象上的三点,则y1,y2,y3的大小关系是( )
B
A. y1
y2=9-6-6=-3,即 y2=-3,
y3=9+6-6=9,即 y3=9,
因为-3<2<9,所以y2<y1<y3.
所以 y1=16-8-6=2,即 y1=2,
课堂练习
比较二次函数值大小的方法:
(1)代入比较法:若已知二次函数的解析式,可将几个点的横坐标分别代入二次函数的解析式,求出对应的函数值,再比较函数值的大小;
(2)增减性比较法:当点都在对称轴的同侧时,可直接根据函数的增减性比较大小,当点不在对称轴的同侧时,可利用二次函数图象的对称性,将点转化到对称轴的同侧,再利用增减性比较大小;
(3)根据点到对称轴的距离比较大小:当抛物线的开口向上时,点到对称轴的距离越大,相应的函数值越大,当抛物线的开口向下时,点到对称轴的距离越大,相应的函数值越小.
2.在平面直角坐标系中,把一条抛物线先向上平移 3 个单位长度,再作关于 x 轴对称的图象,得到抛物线 y=x2+5x+6,则原抛物线的解析式为( )
B
?
?
3.分别在下列范围内求函数 y=x2-2x-3 的最大值和最小值.
(1) -1≤x≤2; (2) 2≤x≤3.
解:因为 y=x2-2x-3=(x-1)2-4,
所以当 x<1 时,y 随 x 的增大而减小,
当 x>1 时,y 随 x 的增大而增大.
(1)由 -1≤x≤2 知,当 x=1时,y 有最小值 -4,
因为当 x=-1 时,y=0,当 x=2 时,y=-3,
所以当 x=-1 时,y 有最大值 0.
(2)当 2≤x≤3时,y 随 x 的增大而增大,
所以当 x=2 时,y 有最小值 -3,当 x=3 时,y 有最大值 0.
求二次函数的最值时,要先确定函数在自变量取值范围内的增减性,如果所给范围包含顶点的横坐标,则在顶点处取得最大(小)值;如果所给范围不包含顶点的横坐标,则利用函数的增减性确定最值.
A.图象与 y 轴的交点坐标为(0,1) B.图象的对称轴在 y 轴的右侧
C.当 x<0 时,y 随 x 的增大而减小 D. y 的最小值为 -3
1.关于二次函数 y=2x2+4x-1,下列说法正确的是( )
D
解:因为y=2x2+4x-1=2(x+1)2-3,
所以当x=0时,y=-1,故选项A错误,
该函数的对称轴是直线x=-1,故选项B错误,
当x<-1时,y随x的增大而减小,故选项C错误,
当x=-1时,y取得最小值,此时y=-3,故选项D正确.
中考实题
A. y3>y2>y1 B. y3>y1=y2 C. y1>y2>y3 D. y1=y2>y3
2.点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数 y=-x2+2x+c 的图象上,则y1,y2,y3 的大小关系是( )
D
解:因为 y=-x2+2x+c=-(x-1)2+1+c,
所以图象的开口向下,对称轴是直线x=1,
而P1(-1,y1)和P2(3,y2)到直线x=1的距离都为2,P3(5,y3)到直线x=1的距离为4,
所以y1=y2>y3.
故选D.
A.①②③ B.②③⑤ C.②③④ D.③④⑤
3.已知二次函数 y=ax2+bx+c(a≠0) 的图象如图所示,有下列 5 个结论:
①abc>0;②b-a>c;③4a+2b+c>0;④3a>-c;⑤a+b>m(am+b)(m≠1).
其中正确的结论有( )
解:①因为对称轴在y轴的右侧,所以ab<0,由图象可知c>0,
所以abc<0,故①不正确;
②当x=-1时,y=a-b+c<0,所以b-a>c,故②正确;
③由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0,故③正确;
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
(顶点式)
归纳新知
a>0
a<0
开口方向
顶点坐标
对称轴
增减性
最值
向上
向下
?
?
?
?
二次函数 y=ax2+bx+c 的图象与性质:
x=
?
A.①②③ B.②③⑤ C.②③④ D.③④⑤
已知二次函数 y=ax2+bx+c(a≠0) 的图象如图所示,有下列 5 个结论:
①abc>0;②b-a>c;③4a+2b+c>0;④3a>-c;⑤a+b>m(am+b)(m≠1).
其中正确的结论有( )
B
再 见
同课章节目录
