人教版数学七年级上册2.2整式的加减-合并同类项 课件1(21张)
文档属性
| 名称 | 人教版数学七年级上册2.2整式的加减-合并同类项 课件1(21张) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 08:09:02 | ||
图片预览







文档简介
求代数式 -4x2+7 x+3 x2-4 x+ x2的值,任意给X取一个小于100的正整数 值,比一比,谁最快得到答案.
一场比赛
一 复习回顾:
1.. -2 ab2的系数 是次数是 ;
2. 组成多项式
的项分别为 , , , , , .
3. 你会计算下列各式的结果吗?
-2
3
4x2
2x
7
3x
-8x
-2
(1)30米+50米=
(2)5个人+8个人=
(3)4条鱼+8个人=
2013.10.11
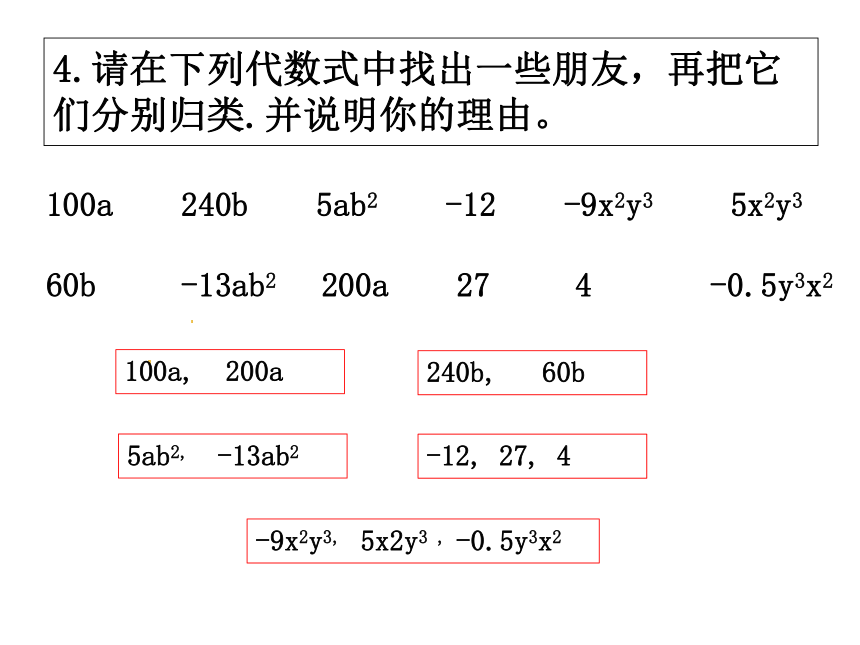
4.请在下列代数式中找出一些朋友,再把它们分别归类.并说明你的理由。
100a 240b 5ab2 -12 -9x2y3 5x2y3
60b -13ab2 200a 27 4 -0.5y3x2
100a, 200a
240b, 60b
5ab2, -13ab2
-12, 27, 4
-9x2y3, 5x2y3 , -0.5y3x2
注:
同类项满足两个条件:
①所含字母相同;
②相同字母的指数相同.
所含字母相同,并且相同字母的指数也相同的项,叫做同类项(liketerms).常数项也是同类项.
同类项的概念
ab2
a2b
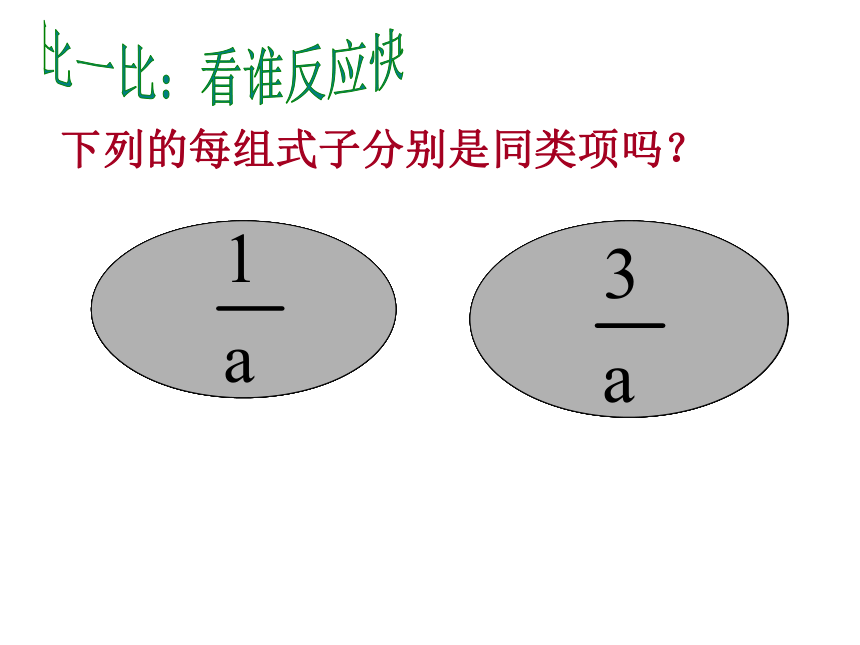
下列的每组式子分别是同类项吗?
-3pq
5pq
abc
ab
25
x5
-x2
Πx2
3×104
-2×103
在下列各对单项式中,同类项有( )个
(1)x和y (2)a2b与ab2
(3)-3pq与3qp (4)bc与ac
(5)a2与a3
(A)1个 (B)2个 (C)3个 (D) 4个
B
你能至少写一对含有2个字母且次数为3的同类项吗?
K取何值时, 与 是同类项?
解:要使 与 是同类项,这两项中x的次数必须相等,即k=2。
所以当k=2时, 与 是同类项。
如果 是同类项,那么 , 。
4
3
探究二:(1)运用有理数的运算律计算.
1.100×2+252×2=( )× =352×2=704 ;
2.100×(-2)+252×(-2)
= ( )×( )
=352×(-2)=-704。
3.100t+252t=( )t=352t
问题3
观察多项式 , , ,
上述多项式的运算有什么共同特点?
你能从中得出什么规律?
合并同类项
合并同类项的法则:
把同类项的系数_____ , 字母和字母的___________.
简记为:(一加,两不变)
相加
指数不变
合并下列各式的同类项:
5x+3x= _____ -3x-8x= _____
ab+ba= _____ 6xy-7xy= _____
合并同类项与单位量的加减法类似
如: 6克 + 7克 = 13克
3 a2b + 5 a2b =8 a2b
8x
-11x
2ab
-xy
整体思想
下列各题合并同类项的结果对不对?若不对,请改正。
(1)、
(2)、
(3)、
(4)、
?
?
?
?
?
?
?
?
=5x2
=4x2
3x与2y不是同类项,不能合并。
例1、合并同类项:
7a-3a2+2a+a2+3
(1)
(2)
步骤:(1)找出同类项(用线画出来);
(2)确定各同类项系数;
(3)合并同类项 ;
(4)单独的项写在后面。(不是同类项不能合并。)
注意:两组同类项之间用“+”连接
求代数式 -4x2+7 x+3 x2-4 x+ x2的值,任意给X取一个小于100的正整数 值,比一比,谁最快得到答案.
刚才的比赛
同 类 项
合并同类项
两个条件
法则
(1)所含字母相同;
(2)相同字母的指数分别相同;
(1)系数相加作为
结果的系数。
(2)字母与字母的
指数不变。
课堂检测:(每题2分,共10分)
1.下面各组中同类项的是( )
A.3a2b3和2b3a2 B.2x2y和2xy2
C.4与a D.2x和2ax
2.下列合并同类项正确的是( )
A.2x2-3x=-x B.2x2-3x2=-1
C.2x2+3x=5x3 D.2x2+5x2=7x2
3.若-3x2y3k+4x2y6结果为单项式, 则k=______
4.填空:-a2b-( )=a2b
5. 化简:7a2-2ab+b2-5a2-b2-2a2-ab。
(1)如果关于字母x的代数式
-3x2 +ax+bx2 +2 x+3合并后不含x的一次项,则下列说法正确的是( )
A. a+b=0 B. a=0
C. b=3 D. a=-2
(2)已知单项式2x6y2m+1与-3x3ny5的差仍是 单项式,则mn的值为
4
D
一场比赛
一 复习回顾:
1.. -2 ab2的系数 是次数是 ;
2. 组成多项式
的项分别为 , , , , , .
3. 你会计算下列各式的结果吗?
-2
3
4x2
2x
7
3x
-8x
-2
(1)30米+50米=
(2)5个人+8个人=
(3)4条鱼+8个人=
2013.10.11
4.请在下列代数式中找出一些朋友,再把它们分别归类.并说明你的理由。
100a 240b 5ab2 -12 -9x2y3 5x2y3
60b -13ab2 200a 27 4 -0.5y3x2
100a, 200a
240b, 60b
5ab2, -13ab2
-12, 27, 4
-9x2y3, 5x2y3 , -0.5y3x2
注:
同类项满足两个条件:
①所含字母相同;
②相同字母的指数相同.
所含字母相同,并且相同字母的指数也相同的项,叫做同类项(liketerms).常数项也是同类项.
同类项的概念
ab2
a2b
下列的每组式子分别是同类项吗?
-3pq
5pq
abc
ab
25
x5
-x2
Πx2
3×104
-2×103
在下列各对单项式中,同类项有( )个
(1)x和y (2)a2b与ab2
(3)-3pq与3qp (4)bc与ac
(5)a2与a3
(A)1个 (B)2个 (C)3个 (D) 4个
B
你能至少写一对含有2个字母且次数为3的同类项吗?
K取何值时, 与 是同类项?
解:要使 与 是同类项,这两项中x的次数必须相等,即k=2。
所以当k=2时, 与 是同类项。
如果 是同类项,那么 , 。
4
3
探究二:(1)运用有理数的运算律计算.
1.100×2+252×2=( )× =352×2=704 ;
2.100×(-2)+252×(-2)
= ( )×( )
=352×(-2)=-704。
3.100t+252t=( )t=352t
问题3
观察多项式 , , ,
上述多项式的运算有什么共同特点?
你能从中得出什么规律?
合并同类项
合并同类项的法则:
把同类项的系数_____ , 字母和字母的___________.
简记为:(一加,两不变)
相加
指数不变
合并下列各式的同类项:
5x+3x= _____ -3x-8x= _____
ab+ba= _____ 6xy-7xy= _____
合并同类项与单位量的加减法类似
如: 6克 + 7克 = 13克
3 a2b + 5 a2b =8 a2b
8x
-11x
2ab
-xy
整体思想
下列各题合并同类项的结果对不对?若不对,请改正。
(1)、
(2)、
(3)、
(4)、
?
?
?
?
?
?
?
?
=5x2
=4x2
3x与2y不是同类项,不能合并。
例1、合并同类项:
7a-3a2+2a+a2+3
(1)
(2)
步骤:(1)找出同类项(用线画出来);
(2)确定各同类项系数;
(3)合并同类项 ;
(4)单独的项写在后面。(不是同类项不能合并。)
注意:两组同类项之间用“+”连接
求代数式 -4x2+7 x+3 x2-4 x+ x2的值,任意给X取一个小于100的正整数 值,比一比,谁最快得到答案.
刚才的比赛
同 类 项
合并同类项
两个条件
法则
(1)所含字母相同;
(2)相同字母的指数分别相同;
(1)系数相加作为
结果的系数。
(2)字母与字母的
指数不变。
课堂检测:(每题2分,共10分)
1.下面各组中同类项的是( )
A.3a2b3和2b3a2 B.2x2y和2xy2
C.4与a D.2x和2ax
2.下列合并同类项正确的是( )
A.2x2-3x=-x B.2x2-3x2=-1
C.2x2+3x=5x3 D.2x2+5x2=7x2
3.若-3x2y3k+4x2y6结果为单项式, 则k=______
4.填空:-a2b-( )=a2b
5. 化简:7a2-2ab+b2-5a2-b2-2a2-ab。
(1)如果关于字母x的代数式
-3x2 +ax+bx2 +2 x+3合并后不含x的一次项,则下列说法正确的是( )
A. a+b=0 B. a=0
C. b=3 D. a=-2
(2)已知单项式2x6y2m+1与-3x3ny5的差仍是 单项式,则mn的值为
4
D
