人教版八年级上册 14.3因式分解(十字相乘法)教学课件(15张)
文档属性
| 名称 | 人教版八年级上册 14.3因式分解(十字相乘法)教学课件(15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 192.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 08:12:22 | ||
图片预览




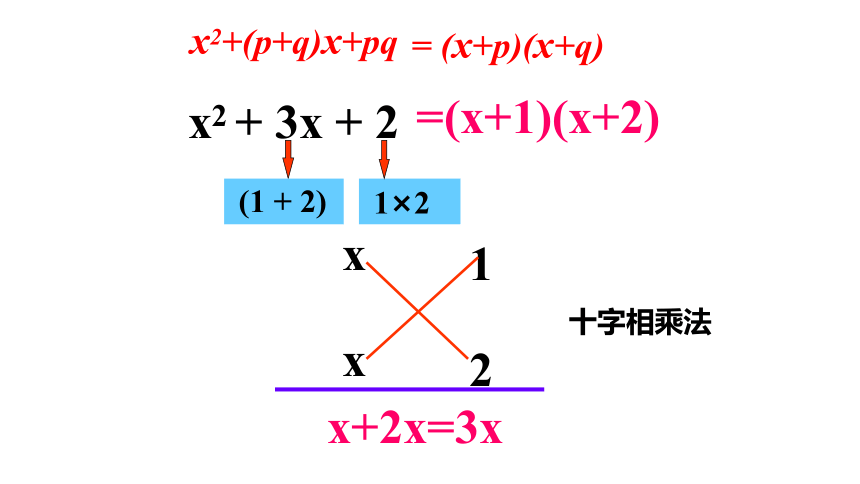


文档简介
14.3因式分解
十字相乘法
课前复习:
1.什么是因式分解?
因式分解的实质是( )与( )是“积化和差”的过程正好( )。
2.之前我们都学习了哪些分解因式的方法?
提取公因式法
公式法
把一个多项式分解成几个整式的积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
“和差化积”
整式乘法
相反
计算:
(1) (x+1)(x+2)
(2) (x+2)(x-1)
(3) (x-2)(x-1)
(4) (x+2)(x+3)
利用公式
(x+p)(x+q) =x2+(p+q)x+pq
=x2+3x+2
=X2+x-2
=x2+5x+6
=x2-3x+2
规律:原式常数项的积=结果中的常数项
原式常数项的和=结果中一次项的系数
等式左边是两个一次二项式( )
二次三项式
右边是( )
相乘
这个过程将( )的形式,转化成( )的形式,进行的是( )运算。
积
和差
整式乘法
x2 + 3x + 2
(1 + 2)
1×2
x
x
1
2
x+2x=3x
=(x+1)(x+2)
x2+(p+q)x+pq
= (x+p)(x+q)
十字相乘法
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫十字相乘法。
十字相乘法
“竖分横积”
四字口诀
十字相乘法公式:
例一:
步骤:
①竖分二次项与常数项
②交叉相乘,和相加
③检验确定,横写因式
十字相乘法(借助十字交叉线分解因式的方法)
顺口溜:
竖分常数交叉验,
横写因式不能乱。
例2 分解因式
X
x
-1
-2
=(x-1)(x-2)
x2-3x+2
(-1)×(-2)=2
(-1)+(-2)= -3
例3 分解因式
X
x
1
-3
=(x+1)(x-3)
x2-2x-3
1×(-3)= -3
1+(-3)= -2
例4:试将
分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
16
6
2
+
-
-
x
x
1. 解题时从哪里入手,凑p还是分解q?
2. 观察前四题,其中的q的符
号有什么共同的特征?
3. 分解后,a、b的符号有一个
什么特征?
4. 那么a、b取正取负又如何
决定?
5. 后面四题的情况呢?
思考:
1.当q〉0时,a、b同号,它们的符号与p相同。
2.当q〈0时,a、b异号,其中绝对值较大的数的符号与p相同。
归纳
练习1把下列各式分解因式
1. x2-11x-12 2. x2+4x-12
3. x2-x-12 4. x2-5x-14
5. y2-11y+24
归纳总结
什么是十字相乘法?
3. 为了快速解题,我们要熟练掌握q、p、a、b的符号之间的联系,请你讲讲有哪些联系。
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫十字相乘法。
2. 运用十字交叉线因式分解时,可以参照四字诀“竖分
横积”,具体操作步骤是怎样的?
1>.当q〉0时,a、b同号,它们的符号与p相同。
2>.当q〈0时,a、b异号,其中绝对值较大的数的符号与p相同。
用十字相乘法分解下列因式
1、x4-13x2+36
2、x2+3xy-4y2
3、x2y2+16xy+48
4、(2+a)2+5(2+a)-36
5、x4-2x3-48x2
2把下列各式分解因式
1、x2-4xy+4y2-6x+12y+8
2、(x2+2x)(x2+2x-11)+11
3、x n+1+3xn+2xn-1
4、(x+1)(x+3)(x+5)(x+7)+16
十字相乘法
课前复习:
1.什么是因式分解?
因式分解的实质是( )与( )是“积化和差”的过程正好( )。
2.之前我们都学习了哪些分解因式的方法?
提取公因式法
公式法
把一个多项式分解成几个整式的积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
“和差化积”
整式乘法
相反
计算:
(1) (x+1)(x+2)
(2) (x+2)(x-1)
(3) (x-2)(x-1)
(4) (x+2)(x+3)
利用公式
(x+p)(x+q) =x2+(p+q)x+pq
=x2+3x+2
=X2+x-2
=x2+5x+6
=x2-3x+2
规律:原式常数项的积=结果中的常数项
原式常数项的和=结果中一次项的系数
等式左边是两个一次二项式( )
二次三项式
右边是( )
相乘
这个过程将( )的形式,转化成( )的形式,进行的是( )运算。
积
和差
整式乘法
x2 + 3x + 2
(1 + 2)
1×2
x
x
1
2
x+2x=3x
=(x+1)(x+2)
x2+(p+q)x+pq
= (x+p)(x+q)
十字相乘法
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫十字相乘法。
十字相乘法
“竖分横积”
四字口诀
十字相乘法公式:
例一:
步骤:
①竖分二次项与常数项
②交叉相乘,和相加
③检验确定,横写因式
十字相乘法(借助十字交叉线分解因式的方法)
顺口溜:
竖分常数交叉验,
横写因式不能乱。
例2 分解因式
X
x
-1
-2
=(x-1)(x-2)
x2-3x+2
(-1)×(-2)=2
(-1)+(-2)= -3
例3 分解因式
X
x
1
-3
=(x+1)(x-3)
x2-2x-3
1×(-3)= -3
1+(-3)= -2
例4:试将
分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
16
6
2
+
-
-
x
x
1. 解题时从哪里入手,凑p还是分解q?
2. 观察前四题,其中的q的符
号有什么共同的特征?
3. 分解后,a、b的符号有一个
什么特征?
4. 那么a、b取正取负又如何
决定?
5. 后面四题的情况呢?
思考:
1.当q〉0时,a、b同号,它们的符号与p相同。
2.当q〈0时,a、b异号,其中绝对值较大的数的符号与p相同。
归纳
练习1把下列各式分解因式
1. x2-11x-12 2. x2+4x-12
3. x2-x-12 4. x2-5x-14
5. y2-11y+24
归纳总结
什么是十字相乘法?
3. 为了快速解题,我们要熟练掌握q、p、a、b的符号之间的联系,请你讲讲有哪些联系。
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫十字相乘法。
2. 运用十字交叉线因式分解时,可以参照四字诀“竖分
横积”,具体操作步骤是怎样的?
1>.当q〉0时,a、b同号,它们的符号与p相同。
2>.当q〈0时,a、b异号,其中绝对值较大的数的符号与p相同。
用十字相乘法分解下列因式
1、x4-13x2+36
2、x2+3xy-4y2
3、x2y2+16xy+48
4、(2+a)2+5(2+a)-36
5、x4-2x3-48x2
2把下列各式分解因式
1、x2-4xy+4y2-6x+12y+8
2、(x2+2x)(x2+2x-11)+11
3、x n+1+3xn+2xn-1
4、(x+1)(x+3)(x+5)(x+7)+16
