六年级上册数学课件-5.4 扇形人教版(共28张PPT)
文档属性
| 名称 | 六年级上册数学课件-5.4 扇形人教版(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
人教版六年级数学上册第五单元4
难点名称:理解扇形的大小在同一个圆中与圆心角的关系,了解扇形与所在圆的关系。
课堂练习
课堂小结
目录
COMTENTS
谈话引入
知识讲解
拓展延伸
像扇子那样形状的图形就是扇形
一、谈话引入
什么是扇形?
二、知识讲解
扇形包含哪些内容呢?
弧、圆心角等
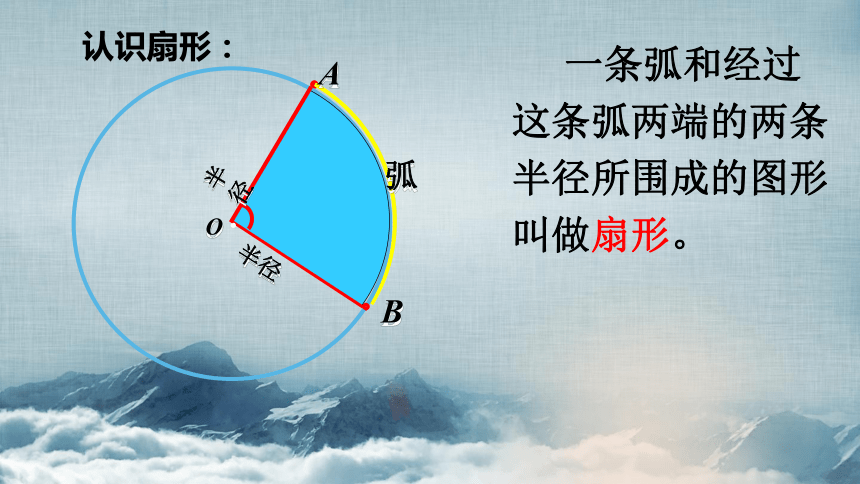
图上A、B两点之间的部分叫做弧,读作“弧AB”。
A
B
O
弧
半径
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
认识扇形:
O
A
B
半径
弧
B
O
圆心角
半径
半径
弧
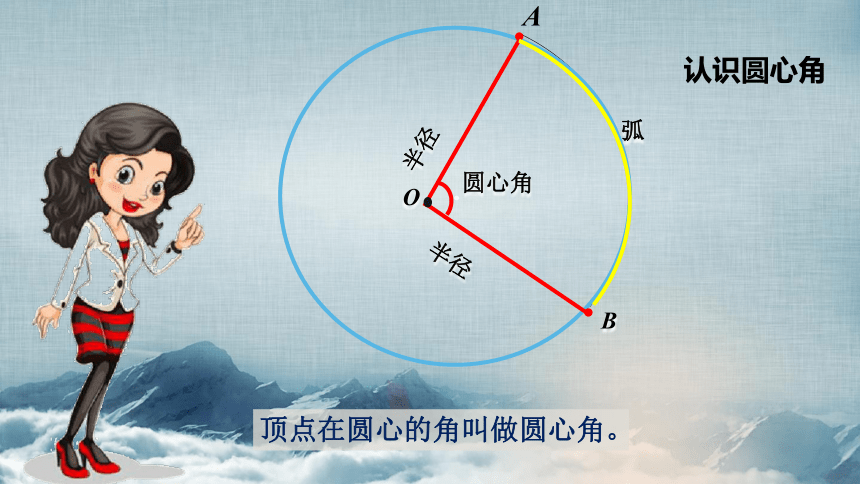
认识圆心角
A
顶点在圆心的角叫做圆心角。
A
B
O
半径
半径
弧
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
圆心角
像∠A0B这样,顶点在圆心的角叫做圆心角。
B
O
A
小结
动手操作:
画一个直径为6厘米的圆,从圆上剪出两个不同的扇形,分别折一折。
圆心角越大,扇形的面积就越大。这种说法你认为正确吗?
扇形的特征
圆心角大,扇形面积不一定大。
扇形的大小与扇形的圆心角的大小有关,还与扇形的半径有关。
当圆心角一定时,扇形的面积随着(
)的增大而增大;
半径
结论
扇形面积大小与(
)和(
)有关。
当半径一定时,扇形的面积随着(
圆心角
)的增大而增大;
当圆心角一定时,扇形的面积随着(
半径
)的增大而增大;
圆心角
半径
同学们对扇形应该有一个比较全面的了解,接下来我们做课堂练习吧。
1.下面图形中涂色的部分,哪些是扇形?
是
否
是
否
否
是
否
否
三、课堂练习
√
2.判断
(1)顶点在圆上的角叫圆心角。(
)
(2)半圆也是一个扇形。(
)
(3)因为扇形是它所在圆的一部分,那么圆上的一部分一定是扇形。(
)
×
×
1.像下图这样一个圆环被截得的部分叫扇环。想一想,怎样求下面扇环的面积?
四、拓展延伸
先算大扇形的面积
3.14×52×
=19.625(dm2)
再算小扇形的面积
3.14×(5-2)2×
=7.065(dm2)
答:扇环的面积是12.56dm2。
扇环的面积是
19.625-7.065=12.56(dm2)
(1)
(2)
先算大半圆的面积
3.14×42×
=25.12(dm2)
再算小半圆的面积
3.14×(4-1)2×
=14.13(dm2)
答:扇环的面积是10.99dm2。
扇环的面积是
25.12-14.13=10.99(dm2)
2.生活中的扇形
汽车轮毂
圆碟上的食物
扇形碟
操场上的推实心球场地
扇形壁画
扇环书画
五、课堂小结
同学们,通过这节课,我们了解了什么是扇形,扇形面积大小与圆心角和半径有关。当半径一定时,扇形的面积随着圆心角的增大而增大;当圆心角一定时,扇形的面积随着半径的增大而增大。扇形在生活中无处不在,希望同学们运用学到的方法去解决生活中的一些问题吧。
人教版六年级数学上册第五单元4
难点名称:理解扇形的大小在同一个圆中与圆心角的关系,了解扇形与所在圆的关系。
课堂练习
课堂小结
目录
COMTENTS
谈话引入
知识讲解
拓展延伸
像扇子那样形状的图形就是扇形
一、谈话引入
什么是扇形?
二、知识讲解
扇形包含哪些内容呢?
弧、圆心角等
图上A、B两点之间的部分叫做弧,读作“弧AB”。
A
B
O
弧
半径
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
认识扇形:
O
A
B
半径
弧
B
O
圆心角
半径
半径
弧
认识圆心角
A
顶点在圆心的角叫做圆心角。
A
B
O
半径
半径
弧
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
圆心角
像∠A0B这样,顶点在圆心的角叫做圆心角。
B
O
A
小结
动手操作:
画一个直径为6厘米的圆,从圆上剪出两个不同的扇形,分别折一折。
圆心角越大,扇形的面积就越大。这种说法你认为正确吗?
扇形的特征
圆心角大,扇形面积不一定大。
扇形的大小与扇形的圆心角的大小有关,还与扇形的半径有关。
当圆心角一定时,扇形的面积随着(
)的增大而增大;
半径
结论
扇形面积大小与(
)和(
)有关。
当半径一定时,扇形的面积随着(
圆心角
)的增大而增大;
当圆心角一定时,扇形的面积随着(
半径
)的增大而增大;
圆心角
半径
同学们对扇形应该有一个比较全面的了解,接下来我们做课堂练习吧。
1.下面图形中涂色的部分,哪些是扇形?
是
否
是
否
否
是
否
否
三、课堂练习
√
2.判断
(1)顶点在圆上的角叫圆心角。(
)
(2)半圆也是一个扇形。(
)
(3)因为扇形是它所在圆的一部分,那么圆上的一部分一定是扇形。(
)
×
×
1.像下图这样一个圆环被截得的部分叫扇环。想一想,怎样求下面扇环的面积?
四、拓展延伸
先算大扇形的面积
3.14×52×
=19.625(dm2)
再算小扇形的面积
3.14×(5-2)2×
=7.065(dm2)
答:扇环的面积是12.56dm2。
扇环的面积是
19.625-7.065=12.56(dm2)
(1)
(2)
先算大半圆的面积
3.14×42×
=25.12(dm2)
再算小半圆的面积
3.14×(4-1)2×
=14.13(dm2)
答:扇环的面积是10.99dm2。
扇环的面积是
25.12-14.13=10.99(dm2)
2.生活中的扇形
汽车轮毂
圆碟上的食物
扇形碟
操场上的推实心球场地
扇形壁画
扇环书画
五、课堂小结
同学们,通过这节课,我们了解了什么是扇形,扇形面积大小与圆心角和半径有关。当半径一定时,扇形的面积随着圆心角的增大而增大;当圆心角一定时,扇形的面积随着半径的增大而增大。扇形在生活中无处不在,希望同学们运用学到的方法去解决生活中的一些问题吧。
