4.2 视图 同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 投影与视图
4.2 视图
知识梳理
知识点1 三视图
人们常常从正面、左面和上面三个不同方向观察一个物体,分别得到这个物体的三种视图.通常我们把从正面得到的视图叫做___________,从左边得到的视图叫做___________,从上面得到的视图叫做___________。
例如,圆柱(图1)、圆锥(图2)、球体(图3)的三视图分别为
知识点2 画三视图的基本要求
(1)在画一个物体的三视图时,主视图与俯视图长对正;主视图与左视图高平齐;俯视图与左视图宽相等,简称“长对正,高平齐,宽相等”。
(2)对于由旋转得到的几何体,画三视图时,通常用点划线表示出它的旋转轴;三视图中的圆通常要用点划线画出水平、竖直两条对称轴.
(3)在画三视图时,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.
考点突破
考点1 三视图的画法
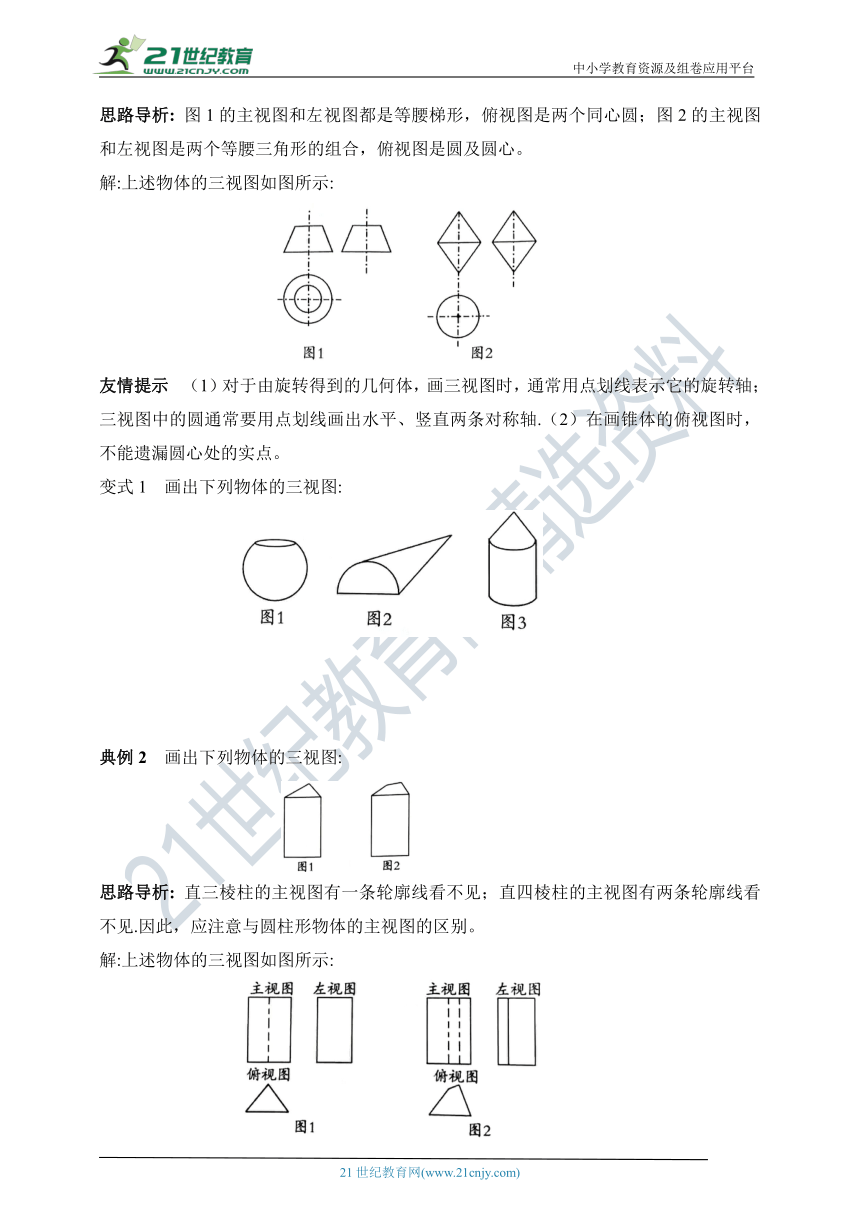
典例1 画出下列物体的三视图:
思路导析: 图1的主视图和左视图都是等腰梯形,俯视图是两个同心圆;图2的主视图和左视图是两个等腰三角形的组合,俯视图是圆及圆心。
解:上述物体的三视图如图所示:
友情提示 (1)对于由旋转得到的几何体,画三视图时,通常用点划线表示它的旋转轴;三视图中的圆通常要用点划线画出水平、竖直两条对称轴.(2)在画锥体的俯视图时,不能遗漏圆心处的实点。
变式1 画出下列物体的三视图:
典例2 画出下列物体的三视图:
思路导析: 直三棱柱的主视图有一条轮廓线看不见;直四棱柱的主视图有两条轮廓线看不见.因此,应注意与圆柱形物体的主视图的区别。
解:上述物体的三视图如图所示:
友情提示 在画视图时,看得见的部分的轮廓线通常画成实线,看不见的部分的轮廓线通常画成虚线,不能漏画了这些轮廓线。
变式2 画出下列物体的三视图:
考点2 根据三视图确定物体的形状
典例3 根据图中某立体图形的三视图,请你判断一下这个立体图形的形状,并画出该立体图形。
思路导析: 在由三视图描述物体的形状时,需要把三个视图结合起来,综合考虑,充分进行空间想象,必要时还可进行实际操作。
解: 该立体图形是正四棱锥,其形状如图所示:
友情提示 在由三视图描述或画立体图形时,大家要充分调动自己的空间想象能力,多联想,综合三视图的特点来对立体图形的形状加以判断。
变式3 如图所示是用几个大小相同的小立方体所搭立体图形的三视图.请你根据所绘图形,画出该立体图形的形状.
巩固提高
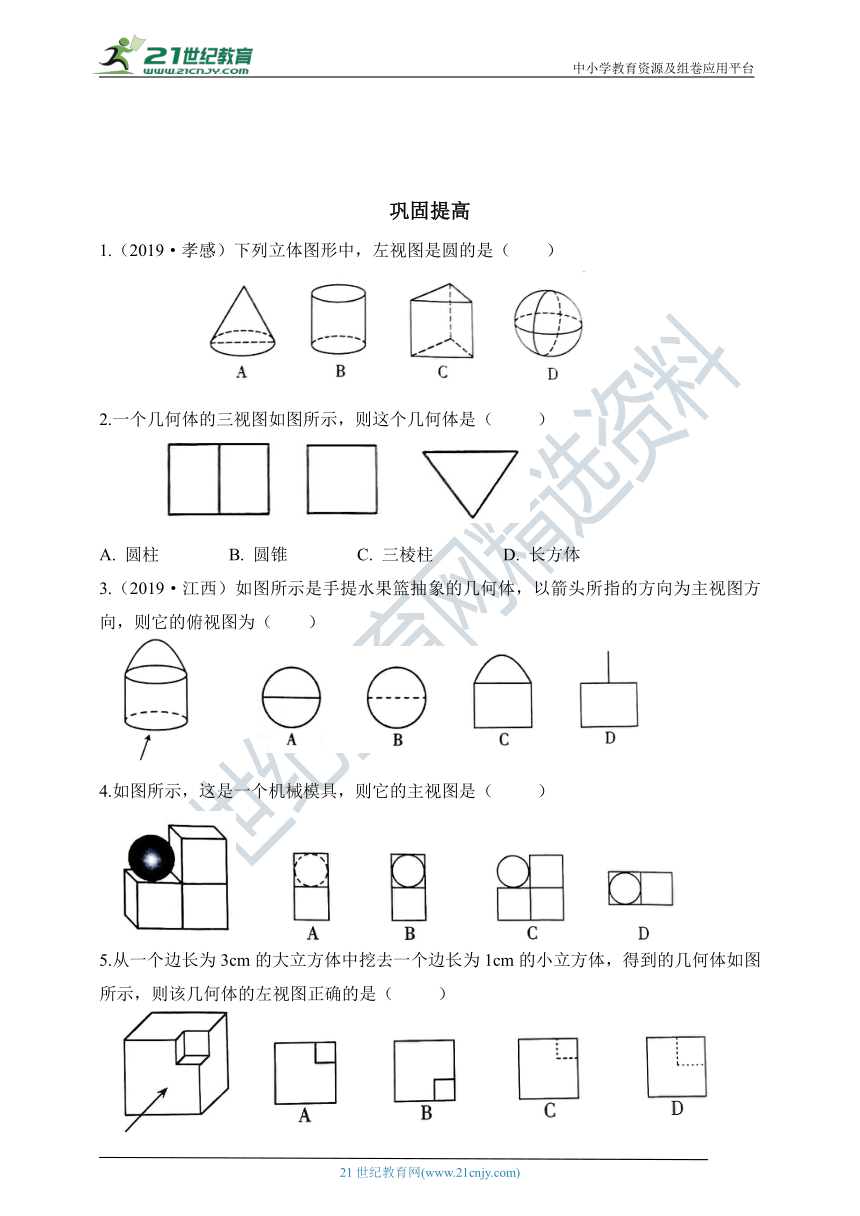
1.(2019·孝感)下列立体图形中,左视图是圆的是( )
2.一个几何体的三视图如图所示,则这个几何体是( )
圆柱 B. 圆锥 C. 三棱柱 D. 长方体
3.(2019·江西)如图所示是手提水果篮抽象的几何体,以箭头所指的方向为主视图方向,则它的俯视图为( )
4.如图所示,这是一个机械模具,则它的主视图是( )
5.从一个边长为3cm的大立方体中挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
6.(2019·安顺)如图所示,该立体图形的俯视图是( )
7.如图所示,在一次数学活动课上,张明用17个边长为1的小正方形搭成一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要____________个小立方体,王亮所搭几何体的表面积为____________。
8.如图所示,是用过正方体上底面的对角线和下底面一顶点的平面将正方体截去一个三棱锥后得到的几何体,请在图中补全它的三视图.
体验中考
1.(2019·恩施州)桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )
2.(2019·济南)以下给出的几何体中,主视图是矩形,俯视图是圆的是( )
3.(2019·大庆)一个“粮仓”的三视图如图所示(单位:m),则它的体积是( )
21πm3 B. 30πm3 C. 45πm3 D. 63πm3
4.(2019·本溪)如图所示,该几何体的左视图是( )
5.(2019·柳州)如图所示,这是一个机械零部件,该零部件的左视图是( )
6.(2019·齐齐哈尔)如图所示是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图,则搭建这个几何体所需要的小正方体的个数至少为( )
5 B. 6 C. 7 D. 8
7.(2019·烟台)如图所示的几何体是由9个大小相同的小正方体组成的,将小正方体①移走后,所得几何体的三视图没有发生变化的是( )
A.主视图和左视图
B.主视图和俯视图
C.左视图和俯视图
D.主视图、左视图、俯视图
8.(2019·张家界)下列四个立体图形中,其主视图是轴对称图形但不是中心对称图形的是( )
9.(2019·荆州)某几何体的三视图如图所示,则下列说法错误的是( )
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D该几何体的表面积为18平方单位
参考答案
知识梳理
知识点1:主视图 左视图 俯视图
考点突破
解:如图所示:
解:如图所示:
解:如图所示:
巩固提高
D 2. C 3. A 4. C 5. C 6. C
19 48
解:如图所示:
体验中考
D 2. D 3. C 4. B 5. C 6. B 7. A 8. C 9. D
_21?????????è?????(www.21cnjy.com)_
第四章 投影与视图
4.2 视图
知识梳理
知识点1 三视图
人们常常从正面、左面和上面三个不同方向观察一个物体,分别得到这个物体的三种视图.通常我们把从正面得到的视图叫做___________,从左边得到的视图叫做___________,从上面得到的视图叫做___________。
例如,圆柱(图1)、圆锥(图2)、球体(图3)的三视图分别为
知识点2 画三视图的基本要求
(1)在画一个物体的三视图时,主视图与俯视图长对正;主视图与左视图高平齐;俯视图与左视图宽相等,简称“长对正,高平齐,宽相等”。
(2)对于由旋转得到的几何体,画三视图时,通常用点划线表示出它的旋转轴;三视图中的圆通常要用点划线画出水平、竖直两条对称轴.
(3)在画三视图时,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.
考点突破
考点1 三视图的画法
典例1 画出下列物体的三视图:
思路导析: 图1的主视图和左视图都是等腰梯形,俯视图是两个同心圆;图2的主视图和左视图是两个等腰三角形的组合,俯视图是圆及圆心。
解:上述物体的三视图如图所示:
友情提示 (1)对于由旋转得到的几何体,画三视图时,通常用点划线表示它的旋转轴;三视图中的圆通常要用点划线画出水平、竖直两条对称轴.(2)在画锥体的俯视图时,不能遗漏圆心处的实点。
变式1 画出下列物体的三视图:
典例2 画出下列物体的三视图:
思路导析: 直三棱柱的主视图有一条轮廓线看不见;直四棱柱的主视图有两条轮廓线看不见.因此,应注意与圆柱形物体的主视图的区别。
解:上述物体的三视图如图所示:
友情提示 在画视图时,看得见的部分的轮廓线通常画成实线,看不见的部分的轮廓线通常画成虚线,不能漏画了这些轮廓线。
变式2 画出下列物体的三视图:
考点2 根据三视图确定物体的形状
典例3 根据图中某立体图形的三视图,请你判断一下这个立体图形的形状,并画出该立体图形。
思路导析: 在由三视图描述物体的形状时,需要把三个视图结合起来,综合考虑,充分进行空间想象,必要时还可进行实际操作。
解: 该立体图形是正四棱锥,其形状如图所示:
友情提示 在由三视图描述或画立体图形时,大家要充分调动自己的空间想象能力,多联想,综合三视图的特点来对立体图形的形状加以判断。
变式3 如图所示是用几个大小相同的小立方体所搭立体图形的三视图.请你根据所绘图形,画出该立体图形的形状.
巩固提高
1.(2019·孝感)下列立体图形中,左视图是圆的是( )
2.一个几何体的三视图如图所示,则这个几何体是( )
圆柱 B. 圆锥 C. 三棱柱 D. 长方体
3.(2019·江西)如图所示是手提水果篮抽象的几何体,以箭头所指的方向为主视图方向,则它的俯视图为( )
4.如图所示,这是一个机械模具,则它的主视图是( )
5.从一个边长为3cm的大立方体中挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
6.(2019·安顺)如图所示,该立体图形的俯视图是( )
7.如图所示,在一次数学活动课上,张明用17个边长为1的小正方形搭成一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要____________个小立方体,王亮所搭几何体的表面积为____________。
8.如图所示,是用过正方体上底面的对角线和下底面一顶点的平面将正方体截去一个三棱锥后得到的几何体,请在图中补全它的三视图.
体验中考
1.(2019·恩施州)桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )
2.(2019·济南)以下给出的几何体中,主视图是矩形,俯视图是圆的是( )
3.(2019·大庆)一个“粮仓”的三视图如图所示(单位:m),则它的体积是( )
21πm3 B. 30πm3 C. 45πm3 D. 63πm3
4.(2019·本溪)如图所示,该几何体的左视图是( )
5.(2019·柳州)如图所示,这是一个机械零部件,该零部件的左视图是( )
6.(2019·齐齐哈尔)如图所示是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图,则搭建这个几何体所需要的小正方体的个数至少为( )
5 B. 6 C. 7 D. 8
7.(2019·烟台)如图所示的几何体是由9个大小相同的小正方体组成的,将小正方体①移走后,所得几何体的三视图没有发生变化的是( )
A.主视图和左视图
B.主视图和俯视图
C.左视图和俯视图
D.主视图、左视图、俯视图
8.(2019·张家界)下列四个立体图形中,其主视图是轴对称图形但不是中心对称图形的是( )
9.(2019·荆州)某几何体的三视图如图所示,则下列说法错误的是( )
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D该几何体的表面积为18平方单位
参考答案
知识梳理
知识点1:主视图 左视图 俯视图
考点突破
解:如图所示:
解:如图所示:
解:如图所示:
巩固提高
D 2. C 3. A 4. C 5. C 6. C
19 48
解:如图所示:
体验中考
D 2. D 3. C 4. B 5. C 6. B 7. A 8. C 9. D
_21?????????è?????(www.21cnjy.com)_
