相似三角形的判定4(AA)
文档属性
| 名称 | 相似三角形的判定4(AA) |  | |
| 格式 | rar | ||
| 文件大小 | 537.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-14 22:29:04 | ||
图片预览



文档简介
(共12张PPT)
(1)我们已学习过哪些判定三角形相似的方法?
(3)如(2)题图,△ABC中,点D在AB上,如果∠ACD=∠B,
那么△ACD与△ABC相似吗?
理由:∵AC2=AD AB
又∠A=∠A
(2)如图,△ABC中,点D在AB上,如果AC2=AD AB,那么△ACD与△ABC相似吗?
说说你的理由.
相似三角形满足对应角相等,对应边的比相等,那么这两个三角形相似.
相似
解:相似
∴△ACD∽△ABC
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
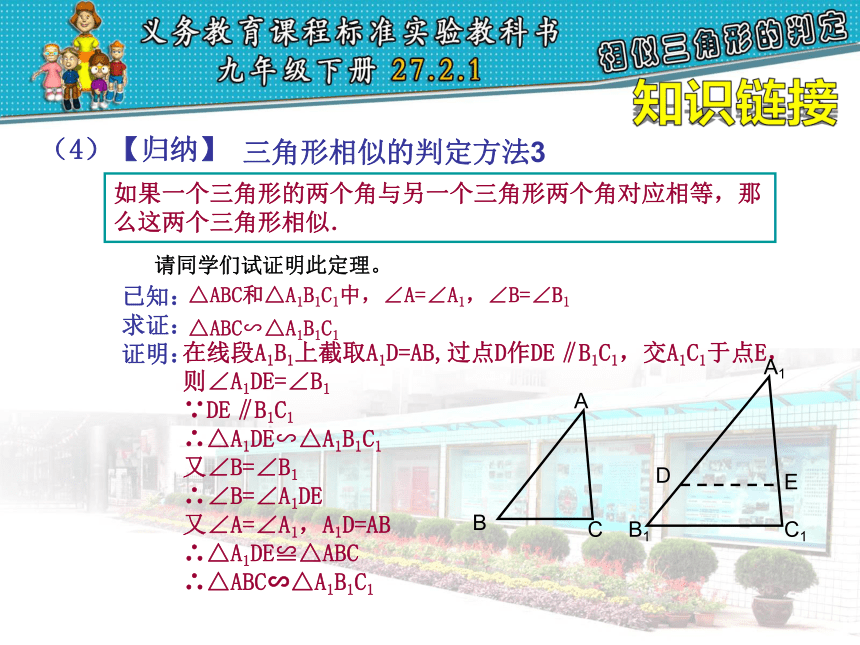
(4)【归纳】
如果一个三角形的两个角与另一个三角形两个角对应相等,那么这两个三角形相似.
在线段A1B1上截取A1D=AB,过点D作DE‖B1C1,交A1C1于点E,
则∠A1DE=∠B1
∵DE‖B1C1
∴△A1DE∽△A1B1C1
又∠B=∠B1
∴∠B=∠A1DE
又∠A=∠A1,A1D=AB
∴△A1DE≌△ABC
∴△ABC∽△A1B1C1
已知:
求证:
证明:
三角形相似的判定方法3
△ABC和△A1B1C1中,∠A=∠A1,∠B=∠B1
△ABC∽△A1B1C1
请同学们试证明此定理。
A
B
C
A1
B1
C1
D
E
A
B
C
D
P
O
分析:要证PA PB=PC PD,需要证:
证明:连接AC、BD
例1(教材P48例2)弦AB和CD相交于⊙O内一点P,求证: PA PB=PC PD.
则需要证明这四条线段所在的两个三角形相似.
∴PA PB=PC PD
∴∠CAB=∠CDB
同理:∠ACD=∠ABD
∴△PAC∽△PDB
∵∠CAB、∠CDB都是弧CB所对的圆周角
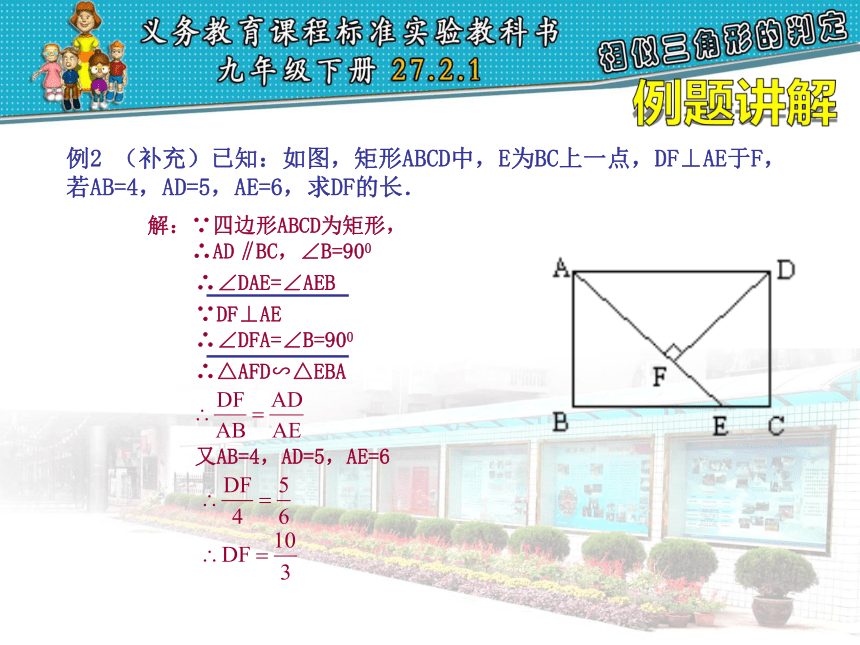
例2 (补充)已知:如图,矩形ABCD中,E为BC上一点,DF⊥AE于F,若AB=4,AD=5,AE=6,求DF的长.
解:∵四边形ABCD为矩形,
∴AD‖BC,∠B=900
∴∠DAE=∠AEB
∴△AFD∽△EBA
又AB=4,AD=5,AE=6
∵DF⊥AE
∴∠DFA=∠B=900
A
B
D
C
图 3
D
A
B
C
E
图 4
1 、填一填
★(1)如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC。
★(2)如图4,已知点E在AC上,若点D在AB上,则满足条件
,就可以使△ADE
与原△ABC相似。
2.下列说法是否正确,并说明理由.
★(1)有一个锐角相等的两直角三角形是相似三角形.( )
★★(2)有一个角相等的两等腰三角形是相似三角形.( )
ACD(ADC)
B(ACB)
∠AED=∠B或∠ADE=∠C或DE‖BC
√
×
★3.如图,△ABC中, DE∥BC,EF∥AB,试说明△ADE∽△EFC.
A
E
F
B
C
D
证明:∵DE∥BC,EF∥AB
∴∠AED=∠C ∠A=∠FEC,
∴△ADE∽△EFC
★★ 4.已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
证明:∵∠1=∠3
∴△ABC∽△ADE
∴∠C=∠E
∵∠2=∠3,∠DOC=∠AOE
∴∠BAC=∠DAE
∴∠1+∠DAC=∠3+∠DAC
★★★5.已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC BC=BE CD;
(2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.
(1)证明:连接EC
∵∠BAC,∠BEC都是劣弧BC所对的圆周角
∴∠BAC=∠BEC
∵CD是△ABC的高
∵BE为圆O的直径
则∠CDA=∠BCE
∴△ACD∽△EBC
(2)解:在Rt△CBD中,CD=6,BD=8
在Rt△ACD中,CD=6,AD=3
∴ AC BC=BE CD
★★★★6、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D ,若E是线段BC中点,ED的延长线交BA的延长线于F,求证:AB : BC=DF : BF.
A
B
D
C
E
F
证明:∵BD⊥AC
∴∠DBC=∠DAB
∴△ABD∽△BCD
∵在Rt△ BCD中,点E为线段BC的中点
∴DE=BE
∴∠EDB=∠DBE
∴∠FBD=∠FDA
又∠F=∠F
∴△FAD∽△FDB
即 AB : BC=DF : BF
∟
作业:课本48练习第2题
(1)我们已学习过哪些判定三角形相似的方法?
(3)如(2)题图,△ABC中,点D在AB上,如果∠ACD=∠B,
那么△ACD与△ABC相似吗?
理由:∵AC2=AD AB
又∠A=∠A
(2)如图,△ABC中,点D在AB上,如果AC2=AD AB,那么△ACD与△ABC相似吗?
说说你的理由.
相似三角形满足对应角相等,对应边的比相等,那么这两个三角形相似.
相似
解:相似
∴△ACD∽△ABC
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
(4)【归纳】
如果一个三角形的两个角与另一个三角形两个角对应相等,那么这两个三角形相似.
在线段A1B1上截取A1D=AB,过点D作DE‖B1C1,交A1C1于点E,
则∠A1DE=∠B1
∵DE‖B1C1
∴△A1DE∽△A1B1C1
又∠B=∠B1
∴∠B=∠A1DE
又∠A=∠A1,A1D=AB
∴△A1DE≌△ABC
∴△ABC∽△A1B1C1
已知:
求证:
证明:
三角形相似的判定方法3
△ABC和△A1B1C1中,∠A=∠A1,∠B=∠B1
△ABC∽△A1B1C1
请同学们试证明此定理。
A
B
C
A1
B1
C1
D
E
A
B
C
D
P
O
分析:要证PA PB=PC PD,需要证:
证明:连接AC、BD
例1(教材P48例2)弦AB和CD相交于⊙O内一点P,求证: PA PB=PC PD.
则需要证明这四条线段所在的两个三角形相似.
∴PA PB=PC PD
∴∠CAB=∠CDB
同理:∠ACD=∠ABD
∴△PAC∽△PDB
∵∠CAB、∠CDB都是弧CB所对的圆周角
例2 (补充)已知:如图,矩形ABCD中,E为BC上一点,DF⊥AE于F,若AB=4,AD=5,AE=6,求DF的长.
解:∵四边形ABCD为矩形,
∴AD‖BC,∠B=900
∴∠DAE=∠AEB
∴△AFD∽△EBA
又AB=4,AD=5,AE=6
∵DF⊥AE
∴∠DFA=∠B=900
A
B
D
C
图 3
D
A
B
C
E
图 4
1 、填一填
★(1)如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC。
★(2)如图4,已知点E在AC上,若点D在AB上,则满足条件
,就可以使△ADE
与原△ABC相似。
2.下列说法是否正确,并说明理由.
★(1)有一个锐角相等的两直角三角形是相似三角形.( )
★★(2)有一个角相等的两等腰三角形是相似三角形.( )
ACD(ADC)
B(ACB)
∠AED=∠B或∠ADE=∠C或DE‖BC
√
×
★3.如图,△ABC中, DE∥BC,EF∥AB,试说明△ADE∽△EFC.
A
E
F
B
C
D
证明:∵DE∥BC,EF∥AB
∴∠AED=∠C ∠A=∠FEC,
∴△ADE∽△EFC
★★ 4.已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
证明:∵∠1=∠3
∴△ABC∽△ADE
∴∠C=∠E
∵∠2=∠3,∠DOC=∠AOE
∴∠BAC=∠DAE
∴∠1+∠DAC=∠3+∠DAC
★★★5.已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC BC=BE CD;
(2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.
(1)证明:连接EC
∵∠BAC,∠BEC都是劣弧BC所对的圆周角
∴∠BAC=∠BEC
∵CD是△ABC的高
∵BE为圆O的直径
则∠CDA=∠BCE
∴△ACD∽△EBC
(2)解:在Rt△CBD中,CD=6,BD=8
在Rt△ACD中,CD=6,AD=3
∴ AC BC=BE CD
★★★★6、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D ,若E是线段BC中点,ED的延长线交BA的延长线于F,求证:AB : BC=DF : BF.
A
B
D
C
E
F
证明:∵BD⊥AC
∴∠DBC=∠DAB
∴△ABD∽△BCD
∵在Rt△ BCD中,点E为线段BC的中点
∴DE=BE
∴∠EDB=∠DBE
∴∠FBD=∠FDA
又∠F=∠F
∴△FAD∽△FDB
即 AB : BC=DF : BF
∟
作业:课本48练习第2题
