22.3 特殊的平行四边形(1) 课件(共28张PPT)
文档属性
| 名称 | 22.3 特殊的平行四边形(1) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 409.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 11:19:23 | ||
图片预览






文档简介
22.3 特殊的平行四边形(1)
三角形的分类
⑴按角分: ①锐角 ②直角 ③钝角
☆直角三角形:有一个内角是直角的三角形叫做直角三角形
⑵按边分:①不等边 ②等腰【等边】
☆等腰三角形:有两边相等的三角形叫做等腰三角形
三角形内角和180°
定义
平行四边形
有一个角是直角的平行四边形叫做矩形
有一个角是直角
矩形
有一组邻边相等的平行四边形叫做菱形
有一组邻边相等
菱形
平行四边形的性质
①平行四边形的对边相等
②平行四边形的对角相等
③平行四边形的两条对角线互相平分
④平行四边形是中心对称图形,
对称中心是两条对角线的交点
四边形内角和360°
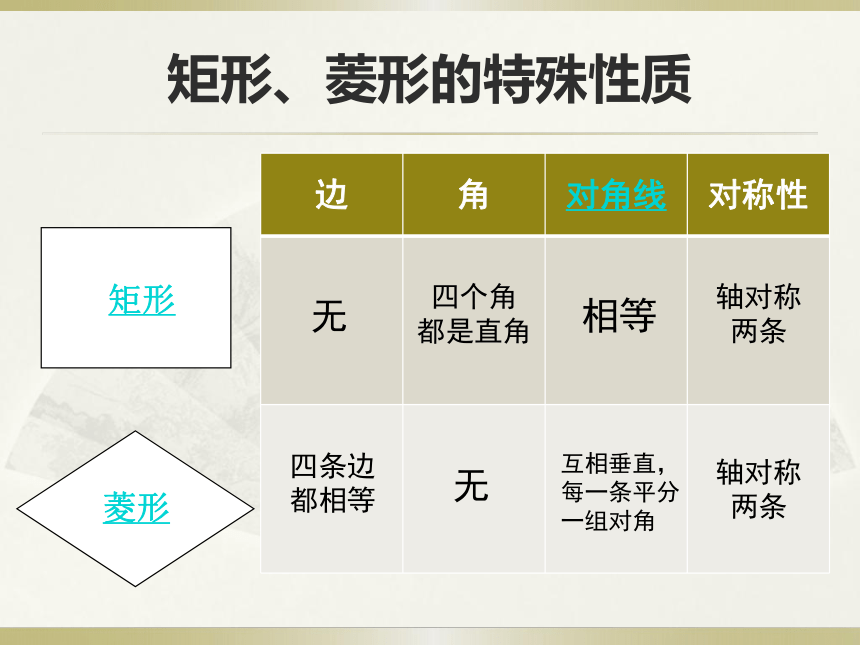
矩形、菱形的特殊性质
矩形
菱形
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}边
角
对角线
对称性
无
四个角
都是直角
四条边都相等
无
相等
互相垂直,每一条平分一组对角
轴对称
两条
轴对称
两条
矩形的性质
①边:矩形的边性质与平行四边形同,无特殊
矩形特有的性质:
②角:矩形四个角都是直角
③对角线:矩形的两条对角线相等
④对称性:矩形是轴对称图形,有两条对称轴,
对称轴分别是两组对边中点连线所在直线
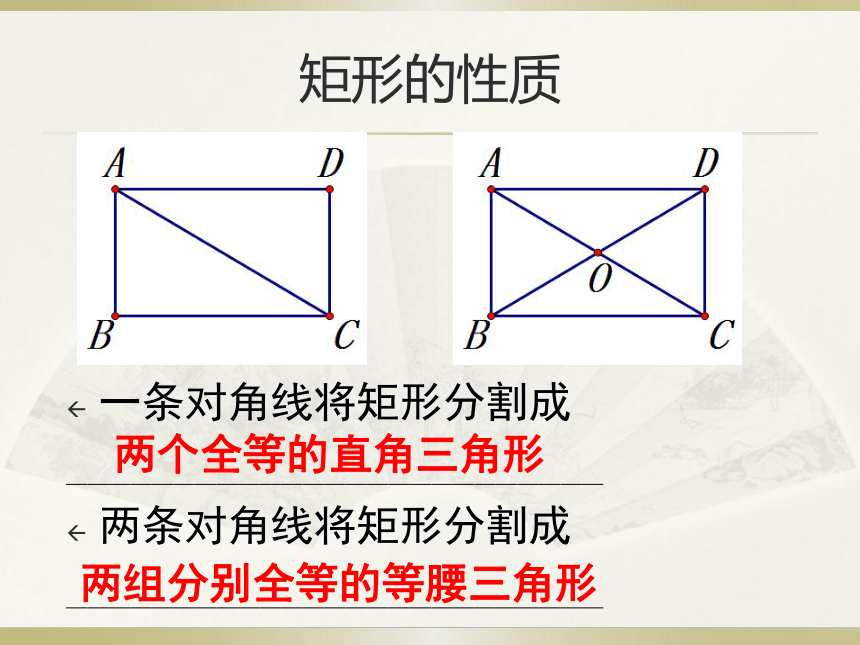
矩形的性质
一条对角线将矩形分割成
_________________________
两条对角线将矩形分割成
_________________________
两个全等的直角三角形
两组分别全等的等腰三角形
菱形的性质
②角: 菱形的角性质与平行四边形同,无特殊
菱形特有的性质:
①边: 菱形的四条边相等
③对角线:菱形的对角线互相垂直,
并且每一条对角线平分一组对角
④对称性:菱形是轴对称图形,有两条对称轴,
对称轴分别是两条对角线所在直线
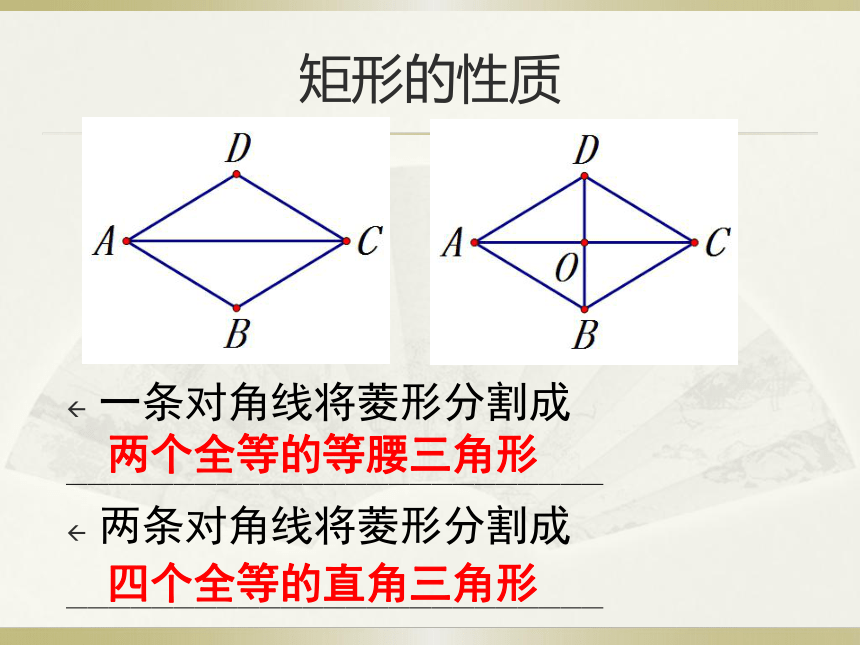
矩形的性质
一条对角线将菱形分割成
_________________________
两条对角线将菱形分割成
_________________________
两个全等的等腰三角形
四个全等的直角三角形
书上P.82
定义:矩形、菱形
矩形性质定理
菱形性质定理
例题1
如图,矩形ABCD的对角线AC与BD相交于点O
已知∠AOD=120°,AB=4cm,
求AC、BD的长
书上P.84练习1
已知:矩形ABCD的对角线AC与BD相交于点O
∠AOB=60°,AB=12cm
求:AC、BD的长
例题2
如图,菱形ABCD的对角线AC与BD相交于点O
已知AB=13cm, AC=24cm
求这个菱形的面积
书上P.84练习2
已知:菱形ABCD的对角线AC与BD相交于点O
求这个菱形的面积
结论
菱形的面积等于对角线长的乘积的一半
书上P.84练习3
已知:菱形ABCD的对角线AC与BD相交于点O
AB=6cm ∠BAD=60°,
求:AC、BD的长
小结
矩形的性质定理
菱形的性质定理
菱形关于对角线的面积公式
例题3
已知:如图,菱形ABCD中, ∠B=60°,点E、F分别在边BC、CD上,且 ∠EAF=60°
求证:AE=AF
22.3(3)矩形、菱形的判定
例题4 已知:矩形ABCD的对角线AC与BD相交于点O,点E、F、G、H分别在AO、BO、CO、DO上,且AE=BF=CG=DH
求证:
四边形EFGH
是矩形
例题5 已知:EF是平行四边形ABCD对角线AC的垂直平分线,
EF与边AD、BC分别交于E、F
求证:四边形AECF是菱形
小结
矩形的判定定理
菱形的判定定理
书上P.87
22.3(4)正方形
定义:有一组邻边相等并且有一个角是直角的
平行四边形叫做正方形
判定1:有一组邻边相等的矩形是正方形
判定2:有一个内角是直角的菱形是正方形
性质1:正方形的四个角都是直角,四条边都相等
性质2:正方形的两条对角线相等,并且互相垂直,每条对角线平分一组对角
例题6 已知:正方形ABCD的、对角线AC、BD相交于点O,
点E在OB的延长线上且∠ECB=15°
求证:△AEC是等边三角形
小结
正方形的定义
正方形判定定理
正方形性质定理
书上P.88
例题7 已知:△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC,DF⊥BC,垂足分别为E、F
求证:四边形CEDF是正方形
例题8 已知:矩形ABCD的四个内角平分线组成四边形EFGH
求证:四边形EFGH是正方形
小结
正方形的定义
正方形判定定理
正方形性质定理
书上P.90
三角形的分类
⑴按角分: ①锐角 ②直角 ③钝角
☆直角三角形:有一个内角是直角的三角形叫做直角三角形
⑵按边分:①不等边 ②等腰【等边】
☆等腰三角形:有两边相等的三角形叫做等腰三角形
三角形内角和180°
定义
平行四边形
有一个角是直角的平行四边形叫做矩形
有一个角是直角
矩形
有一组邻边相等的平行四边形叫做菱形
有一组邻边相等
菱形
平行四边形的性质
①平行四边形的对边相等
②平行四边形的对角相等
③平行四边形的两条对角线互相平分
④平行四边形是中心对称图形,
对称中心是两条对角线的交点
四边形内角和360°
矩形、菱形的特殊性质
矩形
菱形
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}边
角
对角线
对称性
无
四个角
都是直角
四条边都相等
无
相等
互相垂直,每一条平分一组对角
轴对称
两条
轴对称
两条
矩形的性质
①边:矩形的边性质与平行四边形同,无特殊
矩形特有的性质:
②角:矩形四个角都是直角
③对角线:矩形的两条对角线相等
④对称性:矩形是轴对称图形,有两条对称轴,
对称轴分别是两组对边中点连线所在直线
矩形的性质
一条对角线将矩形分割成
_________________________
两条对角线将矩形分割成
_________________________
两个全等的直角三角形
两组分别全等的等腰三角形
菱形的性质
②角: 菱形的角性质与平行四边形同,无特殊
菱形特有的性质:
①边: 菱形的四条边相等
③对角线:菱形的对角线互相垂直,
并且每一条对角线平分一组对角
④对称性:菱形是轴对称图形,有两条对称轴,
对称轴分别是两条对角线所在直线
矩形的性质
一条对角线将菱形分割成
_________________________
两条对角线将菱形分割成
_________________________
两个全等的等腰三角形
四个全等的直角三角形
书上P.82
定义:矩形、菱形
矩形性质定理
菱形性质定理
例题1
如图,矩形ABCD的对角线AC与BD相交于点O
已知∠AOD=120°,AB=4cm,
求AC、BD的长
书上P.84练习1
已知:矩形ABCD的对角线AC与BD相交于点O
∠AOB=60°,AB=12cm
求:AC、BD的长
例题2
如图,菱形ABCD的对角线AC与BD相交于点O
已知AB=13cm, AC=24cm
求这个菱形的面积
书上P.84练习2
已知:菱形ABCD的对角线AC与BD相交于点O
求这个菱形的面积
结论
菱形的面积等于对角线长的乘积的一半
书上P.84练习3
已知:菱形ABCD的对角线AC与BD相交于点O
AB=6cm ∠BAD=60°,
求:AC、BD的长
小结
矩形的性质定理
菱形的性质定理
菱形关于对角线的面积公式
例题3
已知:如图,菱形ABCD中, ∠B=60°,点E、F分别在边BC、CD上,且 ∠EAF=60°
求证:AE=AF
22.3(3)矩形、菱形的判定
例题4 已知:矩形ABCD的对角线AC与BD相交于点O,点E、F、G、H分别在AO、BO、CO、DO上,且AE=BF=CG=DH
求证:
四边形EFGH
是矩形
例题5 已知:EF是平行四边形ABCD对角线AC的垂直平分线,
EF与边AD、BC分别交于E、F
求证:四边形AECF是菱形
小结
矩形的判定定理
菱形的判定定理
书上P.87
22.3(4)正方形
定义:有一组邻边相等并且有一个角是直角的
平行四边形叫做正方形
判定1:有一组邻边相等的矩形是正方形
判定2:有一个内角是直角的菱形是正方形
性质1:正方形的四个角都是直角,四条边都相等
性质2:正方形的两条对角线相等,并且互相垂直,每条对角线平分一组对角
例题6 已知:正方形ABCD的、对角线AC、BD相交于点O,
点E在OB的延长线上且∠ECB=15°
求证:△AEC是等边三角形
小结
正方形的定义
正方形判定定理
正方形性质定理
书上P.88
例题7 已知:△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC,DF⊥BC,垂足分别为E、F
求证:四边形CEDF是正方形
例题8 已知:矩形ABCD的四个内角平分线组成四边形EFGH
求证:四边形EFGH是正方形
小结
正方形的定义
正方形判定定理
正方形性质定理
书上P.90
