27.4 正多边形和圆 课件 (共17页)
文档属性
| 名称 | 27.4 正多边形和圆 课件 (共17页) |

|
|
| 格式 | pptx | ||
| 文件大小 | 342.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 11:15:20 | ||
图片预览





文档简介
27.4 正多边形和圆
九三班
1.了解正多边形和圆的有关概念。
2.理解并掌握正多边形半径、中心角、边心距、边长之间的关系。
3.会应用正多边形和圆的有关知识解决实际问题。
学习目标
学习重难点:
1.重点:多边形的有关概念。
2.难点:利用多边形的有关概念解决实际问题。
图片欣赏
自学提示一:阅读教材65——66页例题前的部分,回答下面问题(8分钟)
问题1 什么叫做正多边形?
问题2 矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
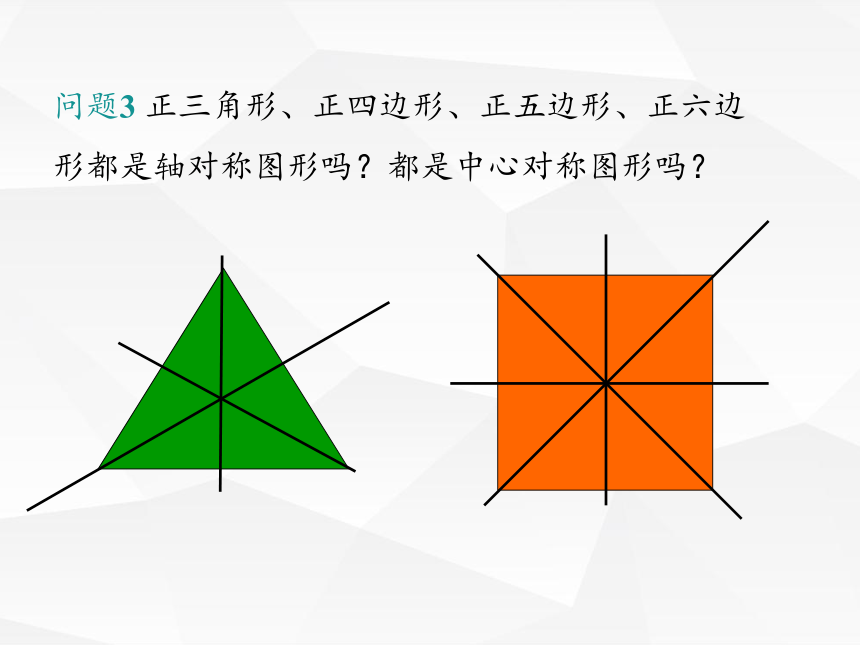
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
问题4 正多边形有怎样的性质,你会证明吗?
问题5什么叫正多形的中心,半径,边心距,中心角
问题1 什么叫做正多边形?
各边相等,各角也相等的多边形叫做正多边形.
问题2 矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
注意
正多边形
各边相等
各角相等
缺一不可
讲授新课
正多边形的对称性
一
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
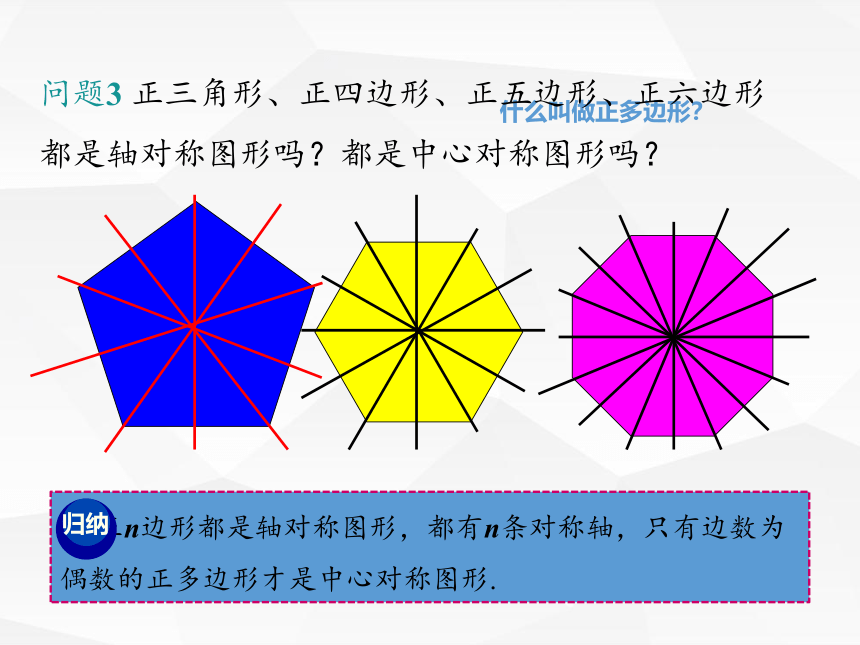
正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形才是中心对称图形.
什么叫做正多边形?
问题1
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
归纳
弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的角相等)
—多边形是正多边形
A
B
C
D
A
B
C
E
F
C
D
.
.
O
中心角
半径R
边心距r
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一条
边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
A
B
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na
R
a
例 有一个亭子它的地基是半径为4m的正六边形,
求地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
.
O
B
C
r
R
P
解:
∴亭子的周长 L=6×4=24(m)
1、正n边形的一个内角的度数是_________;
中心角是___________;
2、正多边形的中心角与外角的大小关系是 ________.
相等
3、正方形ABCD的外接圆圆心
O叫做正方形ABCD的_______.
4、正方形ABCD的内切圆的
半径OE叫做正方形
ABCD的_________.
中心
边心距
.O
A
B
C
D
E
O
5、图中正六边形ABCDEF的中心角是
它的度数是
B
A
E
F
C
D
.O
∠AOB
60度
能力提升
1. 如图,在同心圆中,两圆半径分别为2、1,∠AOB= 120°,则阴影部分的面积为 ( )
A.4π B.2π C.4/3π D.π
B
2. 如图,△ABC为等腰直角三角形,∠A=90°,AB=AC=2,⊙A与BC相切,则图中阴影部分的面积为( )
A.1- B.1-
C.1- D.1-
C
●
A
B
C
D
E
F
3、 如图所示, 已知正六边形ABCDEF的边长为2厘米, 分别以每个顶点为圆心, 以1厘米为半径作弧, 求这些弧所围成的图形(阴影部分)面积.(精确到0.1平方厘米).
H
G
O
课堂小结
正多边形的性质
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正多边形的对称性
再见
九三班
1.了解正多边形和圆的有关概念。
2.理解并掌握正多边形半径、中心角、边心距、边长之间的关系。
3.会应用正多边形和圆的有关知识解决实际问题。
学习目标
学习重难点:
1.重点:多边形的有关概念。
2.难点:利用多边形的有关概念解决实际问题。
图片欣赏
自学提示一:阅读教材65——66页例题前的部分,回答下面问题(8分钟)
问题1 什么叫做正多边形?
问题2 矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
问题4 正多边形有怎样的性质,你会证明吗?
问题5什么叫正多形的中心,半径,边心距,中心角
问题1 什么叫做正多边形?
各边相等,各角也相等的多边形叫做正多边形.
问题2 矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
注意
正多边形
各边相等
各角相等
缺一不可
讲授新课
正多边形的对称性
一
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形才是中心对称图形.
什么叫做正多边形?
问题1
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
归纳
弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的角相等)
—多边形是正多边形
A
B
C
D
A
B
C
E
F
C
D
.
.
O
中心角
半径R
边心距r
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一条
边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
A
B
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na
R
a
例 有一个亭子它的地基是半径为4m的正六边形,
求地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
.
O
B
C
r
R
P
解:
∴亭子的周长 L=6×4=24(m)
1、正n边形的一个内角的度数是_________;
中心角是___________;
2、正多边形的中心角与外角的大小关系是 ________.
相等
3、正方形ABCD的外接圆圆心
O叫做正方形ABCD的_______.
4、正方形ABCD的内切圆的
半径OE叫做正方形
ABCD的_________.
中心
边心距
.O
A
B
C
D
E
O
5、图中正六边形ABCDEF的中心角是
它的度数是
B
A
E
F
C
D
.O
∠AOB
60度
能力提升
1. 如图,在同心圆中,两圆半径分别为2、1,∠AOB= 120°,则阴影部分的面积为 ( )
A.4π B.2π C.4/3π D.π
B
2. 如图,△ABC为等腰直角三角形,∠A=90°,AB=AC=2,⊙A与BC相切,则图中阴影部分的面积为( )
A.1- B.1-
C.1- D.1-
C
●
A
B
C
D
E
F
3、 如图所示, 已知正六边形ABCDEF的边长为2厘米, 分别以每个顶点为圆心, 以1厘米为半径作弧, 求这些弧所围成的图形(阴影部分)面积.(精确到0.1平方厘米).
H
G
O
课堂小结
正多边形的性质
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正多边形的对称性
再见
