9.9利用位似放缩图形(1) 课件 (共30张PPT)
文档属性
| 名称 | 9.9利用位似放缩图形(1) 课件 (共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 11:24:12 | ||
图片预览






文档简介
利用位似放缩图形
O
放映幻灯片时,幻灯机上把缩小的图象放大到屏幕上
放映机
幻灯片放映
利用位似可以将一个图形放大或缩小
教学目标
1、了解位似图形及相关概念,能将图形放大或缩小
2、经历图形的放大或缩小,发展数学应用意识
3、培养积极动手的好习惯,通过探究数学学科知识体会数学实际应用价值和文化价值
?
温故知新
1、什么是相似三角形?
三角分别相等,三边成比例的两个三角形相似
2、什么是相似比
相似三角形对应边的比
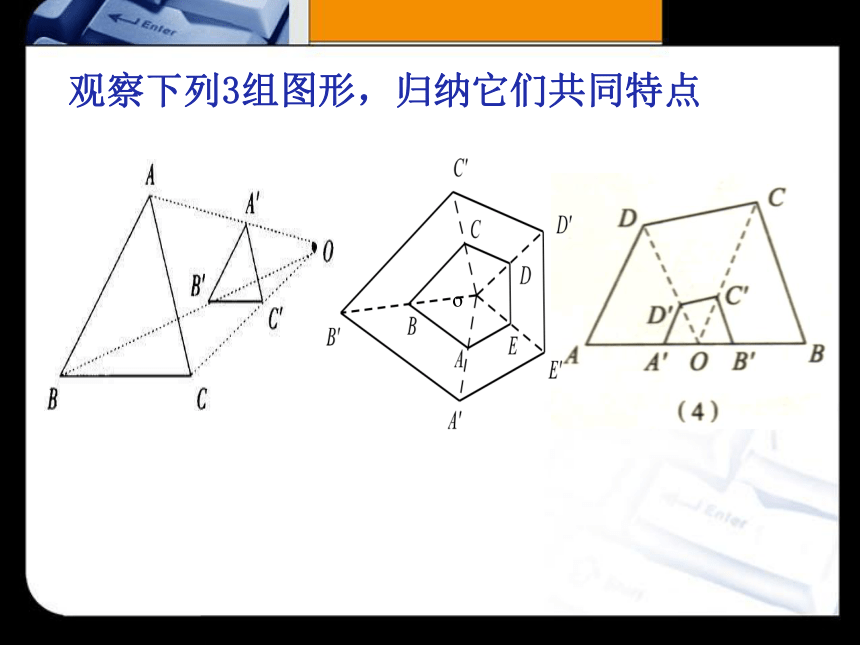
观察下列3组图形,归纳它们共同特点
o
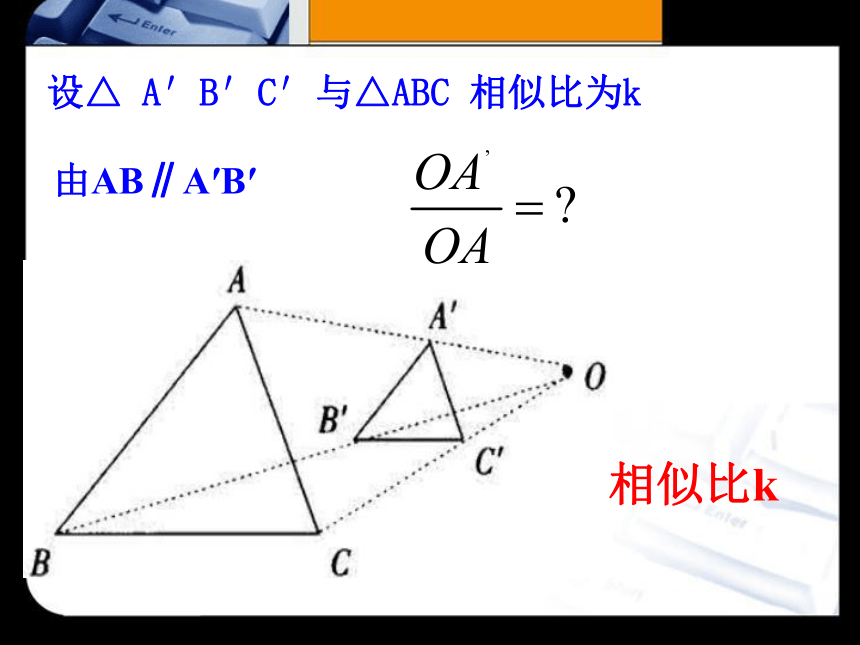
设△ A′B′C′与△ABC 相似比为k
由AB∥A′B′
相似比k
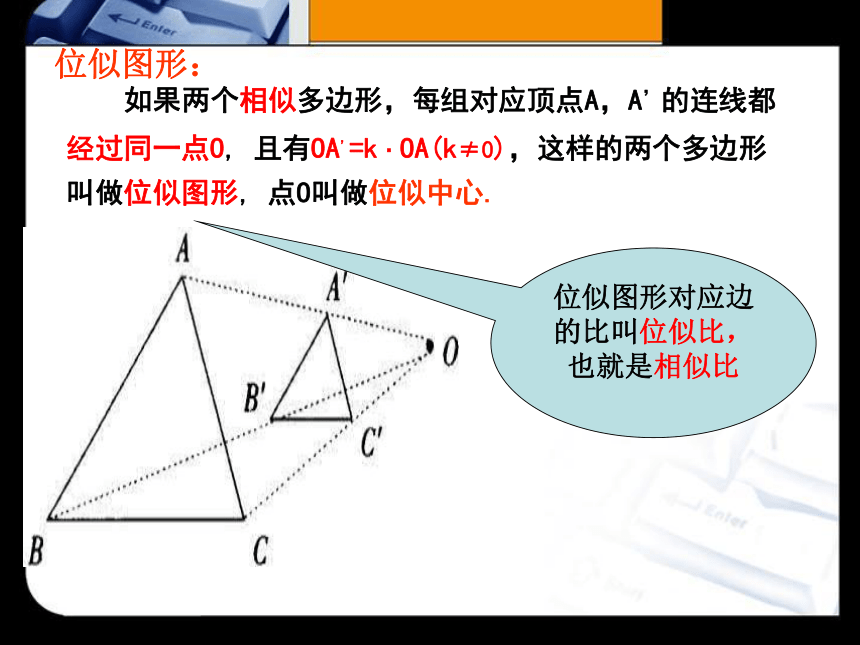
如果两个相似多边形,每组对应顶点A,A,的连线都经过同一点O, 且有OA,=k·OA(k≠0),这样的两个多边形叫做位似图形, 点O叫做位似中心.
位似图形:
位似图形对应边的比叫位似比,也就是相似比
位似图形的性质 (相似比为k):
1.相似图形.
2.对应点连线都交于同一点,
3.对应点与位似中心连线的比等于位似比
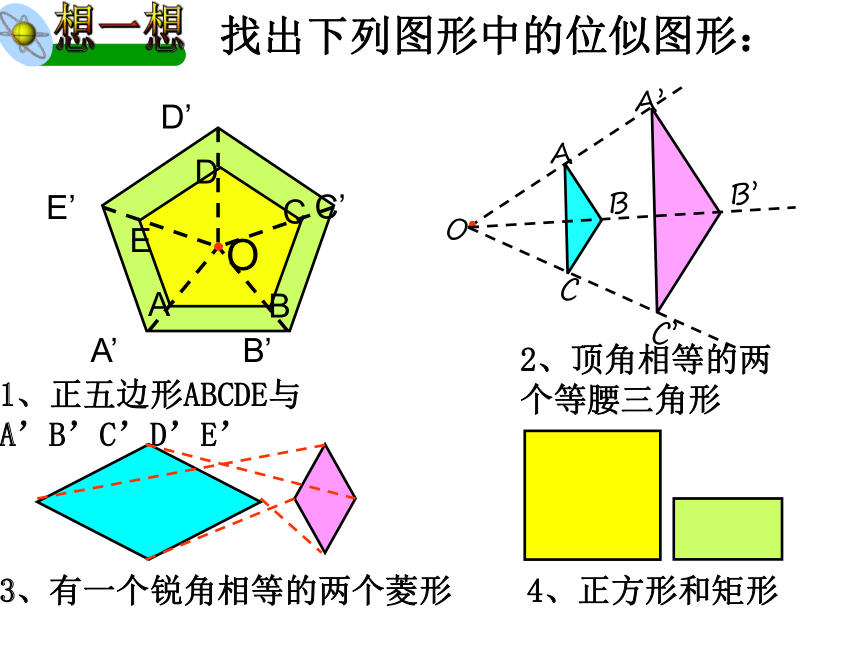
找出下列图形中的位似图形:
A
B
C
D
E
A’
B’
C’
D’
E’
O
A
A’
B
C
B’
C’
O
1、正五边形ABCDE与A’B’C’D’E’
2、顶角相等的两个等腰三角形
3、有一个锐角相等的两个菱形
4、正方形和矩形
辨一辨
1、相似图形一定是位似图形。( )
2、位似图形不一定是相似图形。( )
3、两个图形不是位似图形它们一定不相似( )
4、两个图形不是相似图形一定不位似( )
5、位似图形是特殊的相似图形。( )
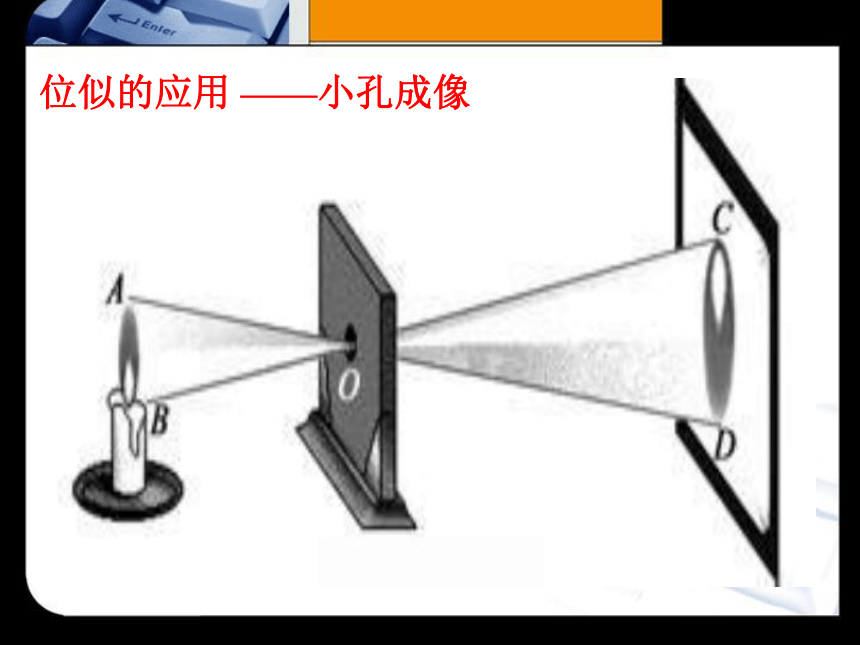
位似的应用 ——小孔成像
O
.
A
B
C
例1.如图,已知△ABC,以O为位似中心,画△A,B,C,,
使它与△ABC位似,且相似比为2
学以致用:画一画
一定在点O的同侧吗?
一展身手:已知:四边形ABCD, 任取一点为位似中心 ,画一个四边形A′B′C′D′,使它与四边形ABCD位似,且相似比为1:2.
你画对了吗?
位似图形作图步骤:
① ;
② ;
③ ;
O
确定位似中心
确定关键点的对应点(依据OA,=k·OA)
顺次连接对应点作图
﹒
﹒
﹒
A
A,
A,
2:3
(1)位似图形上某一对对应点到位似中心的距离分别为4和6,则它们的位似比为( )
拓展提高
(2)如图,P,E,F分别是AC,AB,AD的中点,四边形AEPF
与四边形ABCD是 图形,位似中心是 ,
位似比是 .
位似
点A
1:2
回顾与总结
相似
位似
各组对应点所在的直线交于一点
性质
判断位似
找位似中心
求位似比
作业
必做:伴你学P126
选作:书124页做一做
(制作一个小视频)
不经历风雨,怎么见彩虹
没有人能随随便便便成功!
同学们努力吧!
O
还记得这种变换吗?
A
B
C
D
E
A’
B’
C’
D’
E’
O
A
A’
B
C
B’
C’
O
O
位似的应用 ——小孔成像
点O异侧
O
.
A
B
A'
C’
B’
C
.
(3) 如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交 DC于点E,则图中的位似三角形共有 对.
3
如图,在 ABCD中,F是AD延长线上一点,连接BF交DC于点E,
则图中的位似三角形共有 ( ) 对.
位似图形的性质 (相似比为k):
1.相似图形.
2.对应点连线都交于同一点,
3.对应边互相平行或共线。
4.任意一对对应点A 、A, 有OA,=k·OA
已知:如图,D、E分别是直线AB、AC上的点;
A
B
C
D
E
(2)如果?ADE和 ?ABC是位似图形,那么DE∥BC吗?为什么?
(1)如果DE∥BC,那么?ADE和 ?ABC是位似图形吗?为什么?
D
E
位似图形的对应边互相平行
结论:
或在同一条直线上。
成中心对称的两个三角形
O
O
放映幻灯片时,幻灯机上把缩小的图象放大到屏幕上
放映机
幻灯片放映
利用位似可以将一个图形放大或缩小
教学目标
1、了解位似图形及相关概念,能将图形放大或缩小
2、经历图形的放大或缩小,发展数学应用意识
3、培养积极动手的好习惯,通过探究数学学科知识体会数学实际应用价值和文化价值
?
温故知新
1、什么是相似三角形?
三角分别相等,三边成比例的两个三角形相似
2、什么是相似比
相似三角形对应边的比
观察下列3组图形,归纳它们共同特点
o
设△ A′B′C′与△ABC 相似比为k
由AB∥A′B′
相似比k
如果两个相似多边形,每组对应顶点A,A,的连线都经过同一点O, 且有OA,=k·OA(k≠0),这样的两个多边形叫做位似图形, 点O叫做位似中心.
位似图形:
位似图形对应边的比叫位似比,也就是相似比
位似图形的性质 (相似比为k):
1.相似图形.
2.对应点连线都交于同一点,
3.对应点与位似中心连线的比等于位似比
找出下列图形中的位似图形:
A
B
C
D
E
A’
B’
C’
D’
E’
O
A
A’
B
C
B’
C’
O
1、正五边形ABCDE与A’B’C’D’E’
2、顶角相等的两个等腰三角形
3、有一个锐角相等的两个菱形
4、正方形和矩形
辨一辨
1、相似图形一定是位似图形。( )
2、位似图形不一定是相似图形。( )
3、两个图形不是位似图形它们一定不相似( )
4、两个图形不是相似图形一定不位似( )
5、位似图形是特殊的相似图形。( )
位似的应用 ——小孔成像
O
.
A
B
C
例1.如图,已知△ABC,以O为位似中心,画△A,B,C,,
使它与△ABC位似,且相似比为2
学以致用:画一画
一定在点O的同侧吗?
一展身手:已知:四边形ABCD, 任取一点为位似中心 ,画一个四边形A′B′C′D′,使它与四边形ABCD位似,且相似比为1:2.
你画对了吗?
位似图形作图步骤:
① ;
② ;
③ ;
O
确定位似中心
确定关键点的对应点(依据OA,=k·OA)
顺次连接对应点作图
﹒
﹒
﹒
A
A,
A,
2:3
(1)位似图形上某一对对应点到位似中心的距离分别为4和6,则它们的位似比为( )
拓展提高
(2)如图,P,E,F分别是AC,AB,AD的中点,四边形AEPF
与四边形ABCD是 图形,位似中心是 ,
位似比是 .
位似
点A
1:2
回顾与总结
相似
位似
各组对应点所在的直线交于一点
性质
判断位似
找位似中心
求位似比
作业
必做:伴你学P126
选作:书124页做一做
(制作一个小视频)
不经历风雨,怎么见彩虹
没有人能随随便便便成功!
同学们努力吧!
O
还记得这种变换吗?
A
B
C
D
E
A’
B’
C’
D’
E’
O
A
A’
B
C
B’
C’
O
O
位似的应用 ——小孔成像
点O异侧
O
.
A
B
A'
C’
B’
C
.
(3) 如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交 DC于点E,则图中的位似三角形共有 对.
3
如图,在 ABCD中,F是AD延长线上一点,连接BF交DC于点E,
则图中的位似三角形共有 ( ) 对.
位似图形的性质 (相似比为k):
1.相似图形.
2.对应点连线都交于同一点,
3.对应边互相平行或共线。
4.任意一对对应点A 、A, 有OA,=k·OA
已知:如图,D、E分别是直线AB、AC上的点;
A
B
C
D
E
(2)如果?ADE和 ?ABC是位似图形,那么DE∥BC吗?为什么?
(1)如果DE∥BC,那么?ADE和 ?ABC是位似图形吗?为什么?
D
E
位似图形的对应边互相平行
结论:
或在同一条直线上。
成中心对称的两个三角形
O
