青岛版数学八年级下册课件:7.2 勾股定理(共27张PPT)
文档属性
| 名称 | 青岛版数学八年级下册课件:7.2 勾股定理(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 874.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 11:30:44 | ||
图片预览



文档简介
7.2 勾股定理
学习目标
●了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理
●会用勾股定理进行简单计算,培养严谨的数学学习态度,体会勾股定理的应用价值。
图1(1)
A
C
B
a
c
b
图1(2)
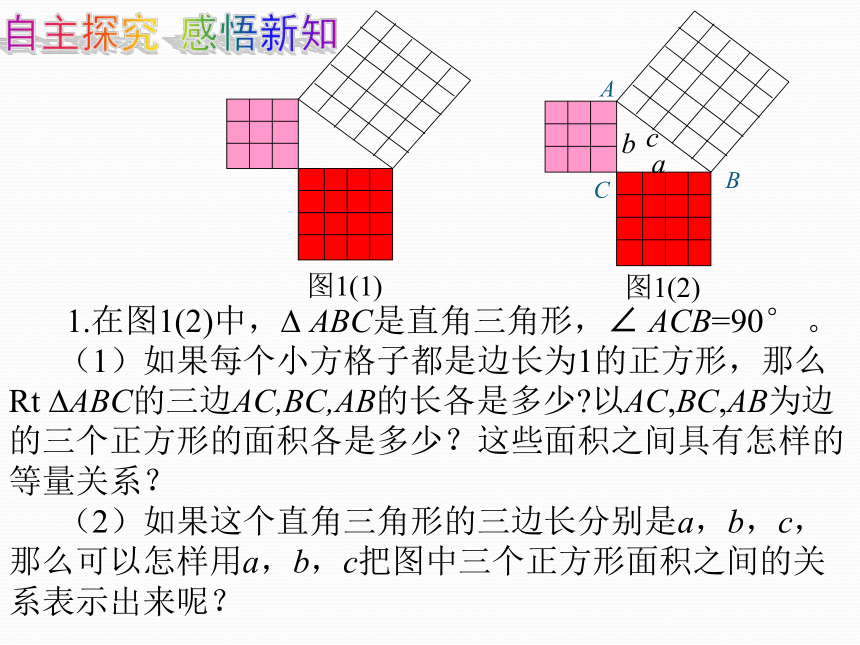
1.在图1(2)中,? ABC是直角三角形,∠ ACB=90° 。
(1)如果每个小方格子都是边长为1的正方形,那么Rt ?ABC的三边AC,BC,AB的长各是多少?以AC,BC,AB为边的三个正方形的面积各是多少?这些面积之间具有怎样的等量关系?
(2)如果这个直角三角形的三边长分别是a,b,c,那么可以怎样用a,b,c把图中三个正方形面积之间的关系表示出来呢?
自主探究 感悟新知
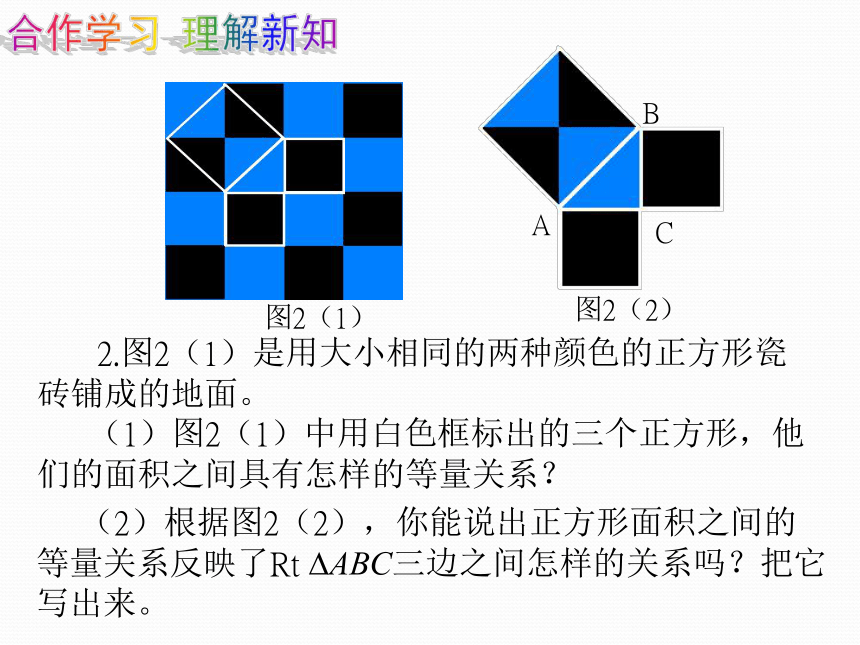
2.图2(1)是用大小相同的两种颜色的正方形瓷 砖铺成的地面。
(1)图2(1)中用白色框标出的三个正方形,他们的面积之间具有怎样的等量关系?
图2(1)
A
B
C
图2(2)
(2)根据图2(2),你能说出正方形面积之间的等量关系反映了Rt ?ABC三边之间怎样的关系吗?把它写出来。
合作学习 理解新知
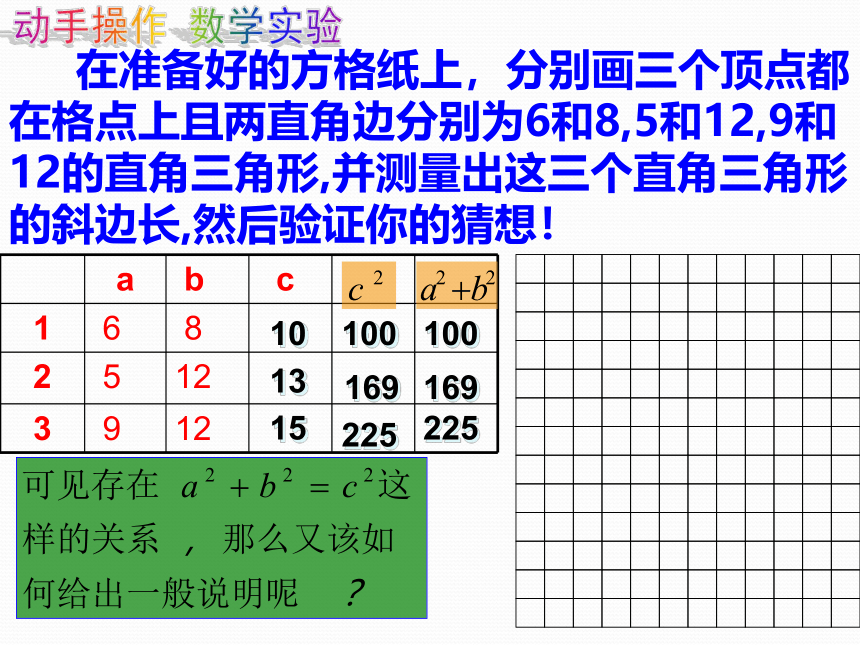
在准备好的方格纸上,分别画三个顶点都在格点上且两直角边分别为6和8,5和12,9和12的直角三角形,并测量出这三个直角三角形的斜边长,然后验证你的猜想!
动手操作 数学实验
a
b
c
1
6
8
2
5
12
3
9
12
15
13
10
225
100
169
225
169
100
c
a
b
1、拿出准备好的四个全等的直角三角形(设直角三角形的两条直角边分别为a,b, 斜边c);
2、你能用这四个直角三角形拼成一个正方形 吗?拼一拼试试看
3、你拼的正方形中是否含有以斜边c的正形?
4、你能否就你拼出的图说明a2+b2=c2?
验证实验 发现规律
PPT模板:www.1ppt.com/moban/ PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/ PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/ 范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/ 教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/ 数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/ 美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/ 物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/ 生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/ 历史课件:www.1ppt.com/kejian/lishi/
a2 + b2 = c2
b
a
c
a
a
b
b
c
Ⅰ
Ⅱ
Ⅲ
a
a
b
b
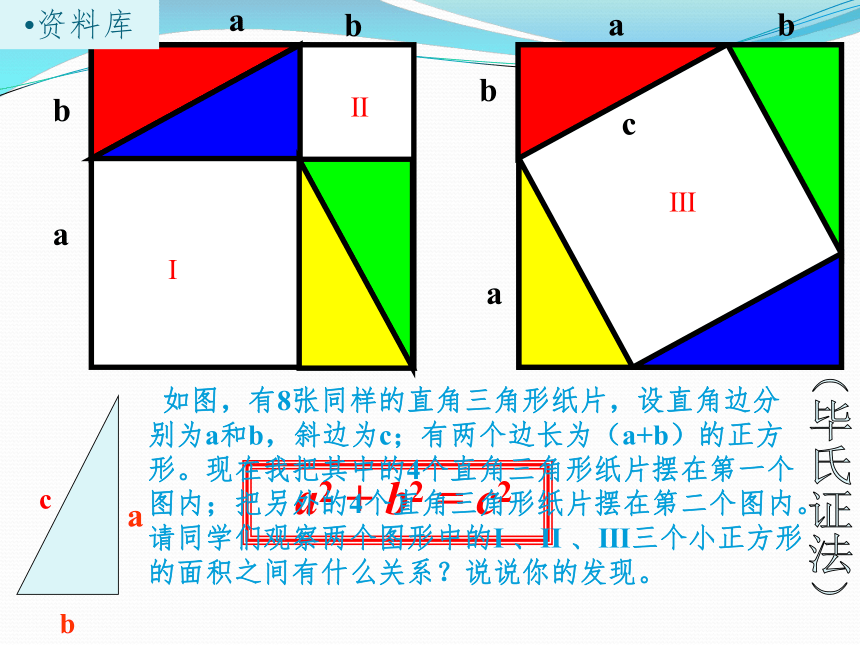
如图,有8张同样的直角三角形纸片,设直角边分别为a和b,斜边为c;有两个边长为(a+b)的正方形。现在我把其中的4个直角三角形纸片摆在第一个图内;把另外的4个直角三角形纸片摆在第二个图内。请同学们观察两个图形中的Ⅰ 、Ⅱ 、Ⅲ三个小正方形的面积之间有什么关系?说说你的发现。
(毕氏证法)
资料库
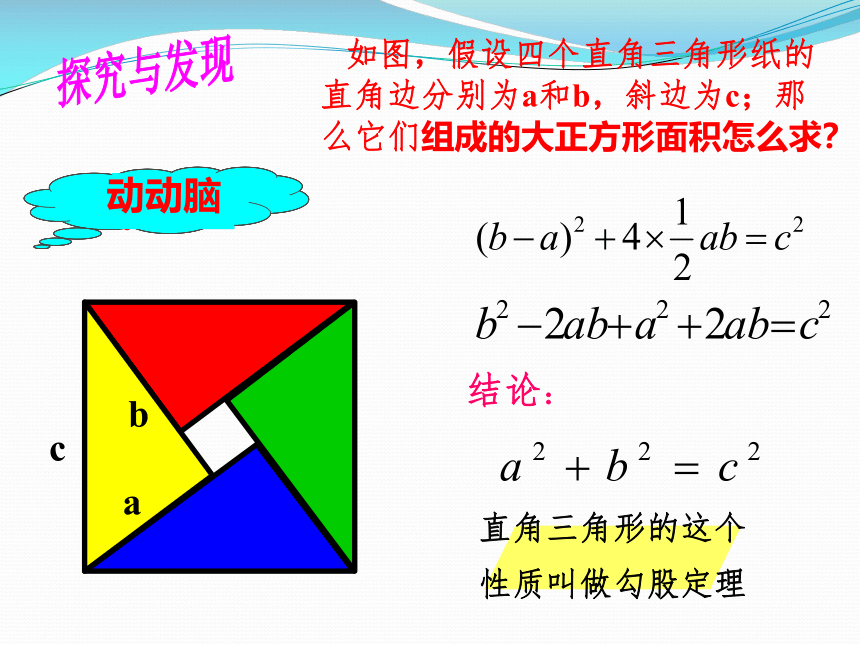
结论:
y=0
如图,假设四个直角三角形纸的直角边分别为a和b,斜边为c;那么它们组成的大正方形面积怎么求?
动动脑
a
b
c
直角三角形的这个
性质叫做勾股定理
探究与发现
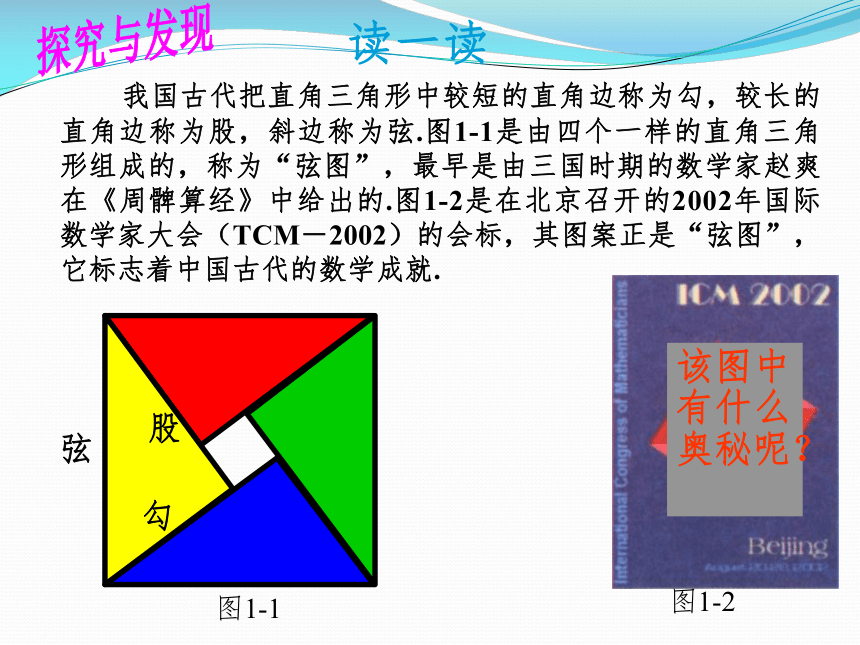
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1是由四个一样的直角三角形组成的,称为“弦图”,最早是由三国时期的数学家赵爽在《周髀算经》中给出的.图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图1-1
图1-2
该图中有什么奥秘呢?
勾
股
弦
探究与发现
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 =
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
C2
证明2:
C2
a
b
c
b
a
c
A
B
C
D
E
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”.
证明3:
你能只用这两个直角三角形说明a2+b2=c2吗?
拼一拼 试一试
勾
股
勾
股
弦
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
辉煌发现
《周髀算经》
毕达哥拉斯
商高
数学史话
《勾股圆方图》
图1
现代汉语的意思是:有一架秋千,当静止时其踏板离地1尺;将它向前推两步(一步指“双步”,即左右脚各迈一步,一步为5尺)并使秋千的绳索拉直,其踏板离地5尺.求绳索的长.
分析:画出如图的图形,由题意可知AC= ;CD= ;CF= .Rt OBF中设OB为x尺,你能解答这个题吗?
1尺
10尺
5尺
解:如图1,设OA为静止时秋千绳索的
长,则
AC=1,CF=5, BF=CD=10. AF=CF-
AC=5-1=4.设
绳索长为OA=OB=x尺。
则 OF=OA-AF=(x-4)尺 在Rt△OBF中,由勾股定理,
得:
OB2=BF2+OF2,即
x2=102+(x-4)2
解得:x=14.5尺 。解得:=14.5尺。
∴绳索长为14.5尺。
O
A
C
B
D
E
F
例2
1) 在直角三角形中,两条直角边分别为a,b, 斜边为c,则c2=____
a2+b2
2) 在RT△ABC中∠C=90°,
⑴若a=4,b=3,则c=____
⑵若c=13,b=5,则a=____
5
12
一 填空题
3) 在直角三角形中,如果有两边 为3,4, 那么另一边为_________
5或 7
⑵如图,在RT△ABC中,∠C=90°,
∠B=45°,AC=1,则AB=( )
A 2, B 1, C , D
A
B
C
⑶一个长 方形的长是宽的2 倍,其对角线的长是5㎝,那么它的宽是( )
A ㎝ B ㎝ C ㎝ D ㎝
1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
C
B
A
1.基础练习之出谋划策
如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?
9m
24m
?
y=0
解除险情
三 解答题
我能行
3、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?
x+1
B
C
A
H
1
2
?
┓
x
x2+22=(x+1)2
2.回归生活之学以致用
100
如图,在Rt△AOB中,∠O=90°,
AO=8米 ,BO=6米,
由勾股定理,得
AB2=AO2+BO2
=82+62=100
于是 AB= =10
所以,钢丝绳的长度为100米.
解
例题学习
例1
如图5—2,从电线杆OA的顶端A点,扯
一根钢丝绳固定在地面上的B点,这根钢
丝绳的长度是多少?
B
O
A
连接OB,OB与OA垂直,得直角三角形,在此直角三角形中,已知两直角边求斜边,应该用勾股定理.
分析:
为什么不用100的平方根呢?
明朝程大位的著作《算法統宗》裏有一道“蕩秋千”的趣題,是用詩歌的形式的:
平地秋千未起,踏板一尺離地;
送行二步與人齊,五尺人高曾記。
仕女佳人爭蹴,終朝笑語歡嬉;
良工高士好奇,算出索長有幾?
趣题欣赏
索長有幾
图1
现代汉语的意思是:有一架秋千,当静止时其踏板离地1尺;将它向前推两步(一步指“双步”,即左右脚各迈一步,一步为5尺)并使秋千的绳索拉直,其踏板离地5尺.求绳索的长.
分析:画出如图的图形,由题意可知AC= ;CD= ;CF= .Rt OBF中设OB为x尺,你能解答这个题吗?
1尺
10尺
5尺
解:如图1,设OA为静止时秋千绳索的
长,则
AC=1,CF=5, BF=CD=10. AF=CF-
AC=5-1=4.设
绳索长为OA=OB=x尺。
则 OF=OA-AF=(x-4)尺 在Rt△OBF中,由勾股定理,
得:
OB2=BF2+OF2,即
x2=102+(x-4)2
解得:x=14.5尺 。解得:=14.5尺。
∴绳索长为14.5尺。
O
A
C
B
D
E
F
例2
如图,将长为10米的梯子AC斜靠 在墙上,BC长为6米。
A
B
C
10
6
(1)求梯子上端A到墙的底端B的距离AB。
(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?
A1
C1
2
3.巩固提高之灵活运用
一个长方形零件(如图),根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
解: 过A作铅垂线,过B作水平线,两线交于点C,则
∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)
由勾股定理有:
AB2=AC2+BC2=502+1202
=16900(mm2)
∵AB>0,
∴AB=130(mm)
答:两孔中心A,B的距离为130mm.
4.应用知识之学海无涯
谈谈你的收获!
勇敢说一说!
1.这节课你的收获是什么?
2.理解“勾股定理”应该注意什么问题?
3.你觉得“勾股定理”有用吗?
要养成用数学的思维去解读世界的习惯。
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步。
其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现在我们的身边,我们的眼前, 还有很多象 “勾股定理”那样的知识等待我们去探索,等待我们去发现……
教师寄语
1.完成课本习题1、2、3(必做)
2.课后小实验:如图,分别以直角三角形的三 边为直径作三个半圆,这三个半圆的面积之间有什么关系?为什么? (必做)
3.做一棵奇妙的勾股树(选做)
作业快餐:
祝同学们学习进步!
再见!
学习目标
●了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理
●会用勾股定理进行简单计算,培养严谨的数学学习态度,体会勾股定理的应用价值。
图1(1)
A
C
B
a
c
b
图1(2)
1.在图1(2)中,? ABC是直角三角形,∠ ACB=90° 。
(1)如果每个小方格子都是边长为1的正方形,那么Rt ?ABC的三边AC,BC,AB的长各是多少?以AC,BC,AB为边的三个正方形的面积各是多少?这些面积之间具有怎样的等量关系?
(2)如果这个直角三角形的三边长分别是a,b,c,那么可以怎样用a,b,c把图中三个正方形面积之间的关系表示出来呢?
自主探究 感悟新知
2.图2(1)是用大小相同的两种颜色的正方形瓷 砖铺成的地面。
(1)图2(1)中用白色框标出的三个正方形,他们的面积之间具有怎样的等量关系?
图2(1)
A
B
C
图2(2)
(2)根据图2(2),你能说出正方形面积之间的等量关系反映了Rt ?ABC三边之间怎样的关系吗?把它写出来。
合作学习 理解新知
在准备好的方格纸上,分别画三个顶点都在格点上且两直角边分别为6和8,5和12,9和12的直角三角形,并测量出这三个直角三角形的斜边长,然后验证你的猜想!
动手操作 数学实验
a
b
c
1
6
8
2
5
12
3
9
12
15
13
10
225
100
169
225
169
100
c
a
b
1、拿出准备好的四个全等的直角三角形(设直角三角形的两条直角边分别为a,b, 斜边c);
2、你能用这四个直角三角形拼成一个正方形 吗?拼一拼试试看
3、你拼的正方形中是否含有以斜边c的正形?
4、你能否就你拼出的图说明a2+b2=c2?
验证实验 发现规律
PPT模板:www.1ppt.com/moban/ PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/ PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/ 范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/ 教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/ 数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/ 美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/ 物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/ 生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/ 历史课件:www.1ppt.com/kejian/lishi/
a2 + b2 = c2
b
a
c
a
a
b
b
c
Ⅰ
Ⅱ
Ⅲ
a
a
b
b
如图,有8张同样的直角三角形纸片,设直角边分别为a和b,斜边为c;有两个边长为(a+b)的正方形。现在我把其中的4个直角三角形纸片摆在第一个图内;把另外的4个直角三角形纸片摆在第二个图内。请同学们观察两个图形中的Ⅰ 、Ⅱ 、Ⅲ三个小正方形的面积之间有什么关系?说说你的发现。
(毕氏证法)
资料库
结论:
y=0
如图,假设四个直角三角形纸的直角边分别为a和b,斜边为c;那么它们组成的大正方形面积怎么求?
动动脑
a
b
c
直角三角形的这个
性质叫做勾股定理
探究与发现
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1是由四个一样的直角三角形组成的,称为“弦图”,最早是由三国时期的数学家赵爽在《周髀算经》中给出的.图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图1-1
图1-2
该图中有什么奥秘呢?
勾
股
弦
探究与发现
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 =
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
C2
证明2:
C2
a
b
c
b
a
c
A
B
C
D
E
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”.
证明3:
你能只用这两个直角三角形说明a2+b2=c2吗?
拼一拼 试一试
勾
股
勾
股
弦
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
辉煌发现
《周髀算经》
毕达哥拉斯
商高
数学史话
《勾股圆方图》
图1
现代汉语的意思是:有一架秋千,当静止时其踏板离地1尺;将它向前推两步(一步指“双步”,即左右脚各迈一步,一步为5尺)并使秋千的绳索拉直,其踏板离地5尺.求绳索的长.
分析:画出如图的图形,由题意可知AC= ;CD= ;CF= .Rt OBF中设OB为x尺,你能解答这个题吗?
1尺
10尺
5尺
解:如图1,设OA为静止时秋千绳索的
长,则
AC=1,CF=5, BF=CD=10. AF=CF-
AC=5-1=4.设
绳索长为OA=OB=x尺。
则 OF=OA-AF=(x-4)尺 在Rt△OBF中,由勾股定理,
得:
OB2=BF2+OF2,即
x2=102+(x-4)2
解得:x=14.5尺 。解得:=14.5尺。
∴绳索长为14.5尺。
O
A
C
B
D
E
F
例2
1) 在直角三角形中,两条直角边分别为a,b, 斜边为c,则c2=____
a2+b2
2) 在RT△ABC中∠C=90°,
⑴若a=4,b=3,则c=____
⑵若c=13,b=5,则a=____
5
12
一 填空题
3) 在直角三角形中,如果有两边 为3,4, 那么另一边为_________
5或 7
⑵如图,在RT△ABC中,∠C=90°,
∠B=45°,AC=1,则AB=( )
A 2, B 1, C , D
A
B
C
⑶一个长 方形的长是宽的2 倍,其对角线的长是5㎝,那么它的宽是( )
A ㎝ B ㎝ C ㎝ D ㎝
1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
C
B
A
1.基础练习之出谋划策
如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?
9m
24m
?
y=0
解除险情
三 解答题
我能行
3、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?
x+1
B
C
A
H
1
2
?
┓
x
x2+22=(x+1)2
2.回归生活之学以致用
100
如图,在Rt△AOB中,∠O=90°,
AO=8米 ,BO=6米,
由勾股定理,得
AB2=AO2+BO2
=82+62=100
于是 AB= =10
所以,钢丝绳的长度为100米.
解
例题学习
例1
如图5—2,从电线杆OA的顶端A点,扯
一根钢丝绳固定在地面上的B点,这根钢
丝绳的长度是多少?
B
O
A
连接OB,OB与OA垂直,得直角三角形,在此直角三角形中,已知两直角边求斜边,应该用勾股定理.
分析:
为什么不用100的平方根呢?
明朝程大位的著作《算法統宗》裏有一道“蕩秋千”的趣題,是用詩歌的形式的:
平地秋千未起,踏板一尺離地;
送行二步與人齊,五尺人高曾記。
仕女佳人爭蹴,終朝笑語歡嬉;
良工高士好奇,算出索長有幾?
趣题欣赏
索長有幾
图1
现代汉语的意思是:有一架秋千,当静止时其踏板离地1尺;将它向前推两步(一步指“双步”,即左右脚各迈一步,一步为5尺)并使秋千的绳索拉直,其踏板离地5尺.求绳索的长.
分析:画出如图的图形,由题意可知AC= ;CD= ;CF= .Rt OBF中设OB为x尺,你能解答这个题吗?
1尺
10尺
5尺
解:如图1,设OA为静止时秋千绳索的
长,则
AC=1,CF=5, BF=CD=10. AF=CF-
AC=5-1=4.设
绳索长为OA=OB=x尺。
则 OF=OA-AF=(x-4)尺 在Rt△OBF中,由勾股定理,
得:
OB2=BF2+OF2,即
x2=102+(x-4)2
解得:x=14.5尺 。解得:=14.5尺。
∴绳索长为14.5尺。
O
A
C
B
D
E
F
例2
如图,将长为10米的梯子AC斜靠 在墙上,BC长为6米。
A
B
C
10
6
(1)求梯子上端A到墙的底端B的距离AB。
(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?
A1
C1
2
3.巩固提高之灵活运用
一个长方形零件(如图),根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
解: 过A作铅垂线,过B作水平线,两线交于点C,则
∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)
由勾股定理有:
AB2=AC2+BC2=502+1202
=16900(mm2)
∵AB>0,
∴AB=130(mm)
答:两孔中心A,B的距离为130mm.
4.应用知识之学海无涯
谈谈你的收获!
勇敢说一说!
1.这节课你的收获是什么?
2.理解“勾股定理”应该注意什么问题?
3.你觉得“勾股定理”有用吗?
要养成用数学的思维去解读世界的习惯。
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步。
其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现在我们的身边,我们的眼前, 还有很多象 “勾股定理”那样的知识等待我们去探索,等待我们去发现……
教师寄语
1.完成课本习题1、2、3(必做)
2.课后小实验:如图,分别以直角三角形的三 边为直径作三个半圆,这三个半圆的面积之间有什么关系?为什么? (必做)
3.做一棵奇妙的勾股树(选做)
作业快餐:
祝同学们学习进步!
再见!
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
