人教版八年级数学下册课件:17.1 第3课时 勾股定理作图与计算(19张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:17.1 第3课时 勾股定理作图与计算(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 11:24:57 | ||
图片预览




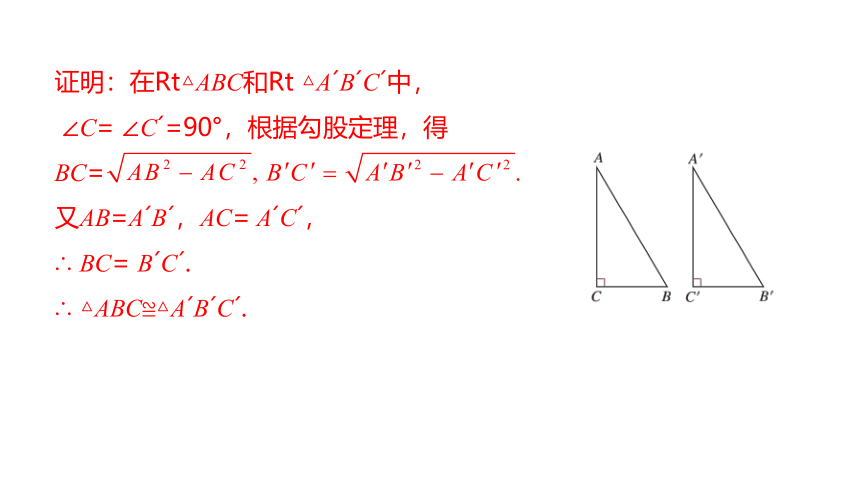

文档简介
第十七章 勾股定理
17.1 第3课时 勾股定理作图与计算
情景导入
欣赏下面海螺的图片:
在数学中也有这样一幅美丽的“海螺型”图案,
如第七届国际数学教育大会的会徽.
这个图是怎样绘制出来的呢?
知识回顾
回忆八年级上册学习的HL定理的内容.
斜边和一条直角边对应相等的两个直角三角形全等.
学习了勾股定理后,你可以证明这个定理吗?
获取新知
知识点一:HL的证明和应用
先画出图形,写出已知、求证如下:
已知:如图,在Rt△ABC和Rt△A?B?C?中,∠C=∠C?=90°,AB=A?B?,AC=A?C?.
求证:△ABC≌△A?B?C?(SSS).
证明:在Rt△ABC和Rt △A?B?C?中,
∠C= ∠C?=90°,根据勾股定理,得
BC=
又AB=A?B?,AC= A?C?,
∴ BC= B?C?.
∴ △ABC≌△A?B?C?.
例题讲解
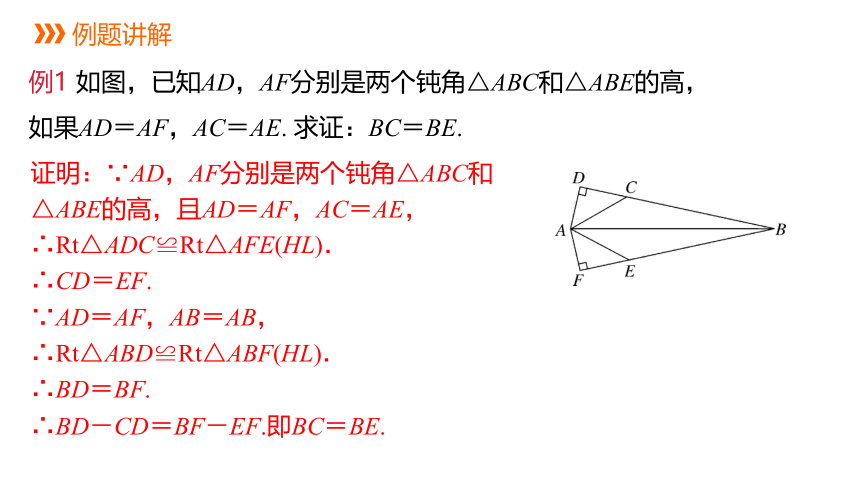
例1 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
获取新知
知识点二:利用勾股定理来作图
我们知道数轴上的点有的表示有理数,有的表示无理
数,你能在数轴 上画出表示 的点吗?
如果能画出长为 的线段,就能在数轴上画出表示
的点.容易知道,长为 的线段是两条直角边的长都
为1的直角三角形的斜边.长为 的线段能是直角边的长
为正整数的直角三角形的斜边吗?
利用勾股定理,可以发现,直角边的长为正整数2, 3
的直角三角形的斜边长为 .由此,可以依照如下方法在
数轴上画出表示 的点:
步骤:
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交
于C点,则点C即为表示 的点.
l
A
B
4
0
1
2
3
C
O
也可以使OA=2,AB=3,同样可以求出C点.
图1
图2
类似地,利用勾股定理,可以作出长为 …
的线段(图1).按照同样方法,可以在数轴上画出表示 …的点 (图 2).
“数学海螺”
例题讲解
例2 你能在数轴上画出表示 的点吗?
l
A
B
C
0
1
2
3
4
解:如图所示.作法:
(1)在数轴上找出表示4(或1)的点A,则OA=4(或1);
(2)过A作直线l垂直于OA;
(3)在直线l上取点B,使AB=1(或4);
(4)以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
随堂演练
1. 如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt △ABC与Rt △ABD全等.以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
2.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:如图,首先画出数轴,设原点为点O,在数轴上距原点2个单位长度的位置找一个点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB长为半径作弧,与数轴右侧的交点记为点P,则点P表示的实数在( )
A.1和2之间
B.2和3之间
C.3和4之间
D.4和5之间
C
3. 如图,网格中每个小正方形的边长都为1,
则△ABC的周长为( )
B
4. 如图所示,在正方形ODBC中,OC=2,OA=OB,则数轴上点A表示的数是_____.
5. 如图是由4个边长为1的正方形构成的“田字格”,只用没有刻度的直尺在这个“田字格”中最多可以作出长度为 的线段____条.
8
6. 请在如图所示的数轴上作出 对应的点.
解:如图所示,点C即为 对应的点,
点F即为 对应的点
7. 如图,折叠长方形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8 cm,BC=10 cm,求CE的长.
解:由题意,知BC=AD=AF=10 cm,DE=EF.
在Rt△ABF中,BF= (cm),
∴CF=BC-BF=4 cm.
设CE=x cm,则DE=EF=(8-x)cm.
在Rt△FEC中, 由勾股定理,
得CF2+CE2=EF2,即42+x2=(8-x)2,
解得x=3,即CE=3 cm.
课堂小结
利用勾股定理
作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来
通常用到方程思想
17.1 第3课时 勾股定理作图与计算
情景导入
欣赏下面海螺的图片:
在数学中也有这样一幅美丽的“海螺型”图案,
如第七届国际数学教育大会的会徽.
这个图是怎样绘制出来的呢?
知识回顾
回忆八年级上册学习的HL定理的内容.
斜边和一条直角边对应相等的两个直角三角形全等.
学习了勾股定理后,你可以证明这个定理吗?
获取新知
知识点一:HL的证明和应用
先画出图形,写出已知、求证如下:
已知:如图,在Rt△ABC和Rt△A?B?C?中,∠C=∠C?=90°,AB=A?B?,AC=A?C?.
求证:△ABC≌△A?B?C?(SSS).
证明:在Rt△ABC和Rt △A?B?C?中,
∠C= ∠C?=90°,根据勾股定理,得
BC=
又AB=A?B?,AC= A?C?,
∴ BC= B?C?.
∴ △ABC≌△A?B?C?.
例题讲解
例1 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
获取新知
知识点二:利用勾股定理来作图
我们知道数轴上的点有的表示有理数,有的表示无理
数,你能在数轴 上画出表示 的点吗?
如果能画出长为 的线段,就能在数轴上画出表示
的点.容易知道,长为 的线段是两条直角边的长都
为1的直角三角形的斜边.长为 的线段能是直角边的长
为正整数的直角三角形的斜边吗?
利用勾股定理,可以发现,直角边的长为正整数2, 3
的直角三角形的斜边长为 .由此,可以依照如下方法在
数轴上画出表示 的点:
步骤:
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交
于C点,则点C即为表示 的点.
l
A
B
4
0
1
2
3
C
O
也可以使OA=2,AB=3,同样可以求出C点.
图1
图2
类似地,利用勾股定理,可以作出长为 …
的线段(图1).按照同样方法,可以在数轴上画出表示 …的点 (图 2).
“数学海螺”
例题讲解
例2 你能在数轴上画出表示 的点吗?
l
A
B
C
0
1
2
3
4
解:如图所示.作法:
(1)在数轴上找出表示4(或1)的点A,则OA=4(或1);
(2)过A作直线l垂直于OA;
(3)在直线l上取点B,使AB=1(或4);
(4)以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
随堂演练
1. 如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt △ABC与Rt △ABD全等.以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
2.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:如图,首先画出数轴,设原点为点O,在数轴上距原点2个单位长度的位置找一个点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB长为半径作弧,与数轴右侧的交点记为点P,则点P表示的实数在( )
A.1和2之间
B.2和3之间
C.3和4之间
D.4和5之间
C
3. 如图,网格中每个小正方形的边长都为1,
则△ABC的周长为( )
B
4. 如图所示,在正方形ODBC中,OC=2,OA=OB,则数轴上点A表示的数是_____.
5. 如图是由4个边长为1的正方形构成的“田字格”,只用没有刻度的直尺在这个“田字格”中最多可以作出长度为 的线段____条.
8
6. 请在如图所示的数轴上作出 对应的点.
解:如图所示,点C即为 对应的点,
点F即为 对应的点
7. 如图,折叠长方形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8 cm,BC=10 cm,求CE的长.
解:由题意,知BC=AD=AF=10 cm,DE=EF.
在Rt△ABF中,BF= (cm),
∴CF=BC-BF=4 cm.
设CE=x cm,则DE=EF=(8-x)cm.
在Rt△FEC中, 由勾股定理,
得CF2+CE2=EF2,即42+x2=(8-x)2,
解得x=3,即CE=3 cm.
课堂小结
利用勾股定理
作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来
通常用到方程思想
