人教版九年级数学下册27.2.1:两角判定法 课件(21张PPT)
文档属性
| 名称 | 人教版九年级数学下册27.2.1:两角判定法 课件(21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 11:43:03 | ||
图片预览





文档简介
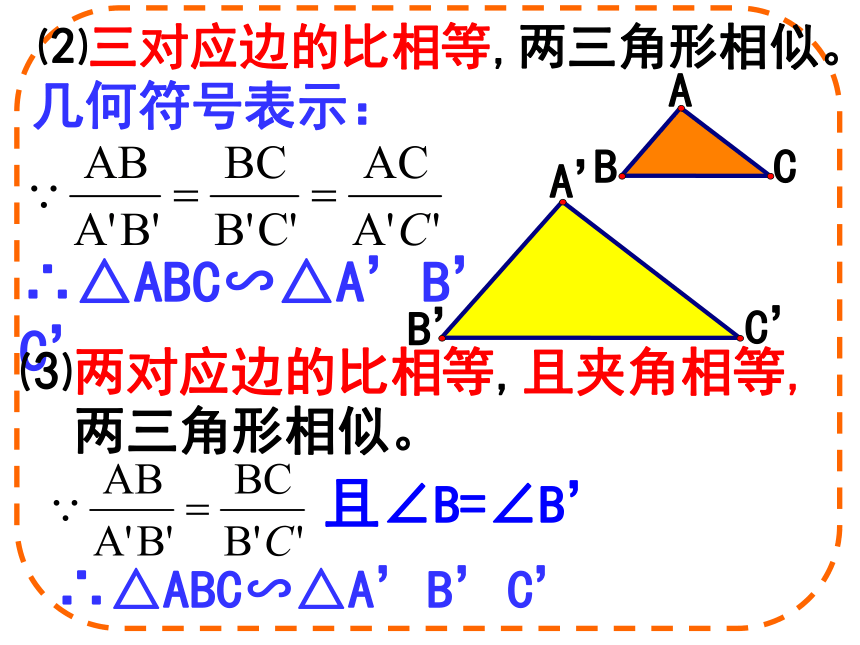
∵DE∥BC
∴△ADE∽△ABC
⑴平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
D
E
A
B
C
A
B
C
D
E
几何符号表示:
相似三角形的判定:
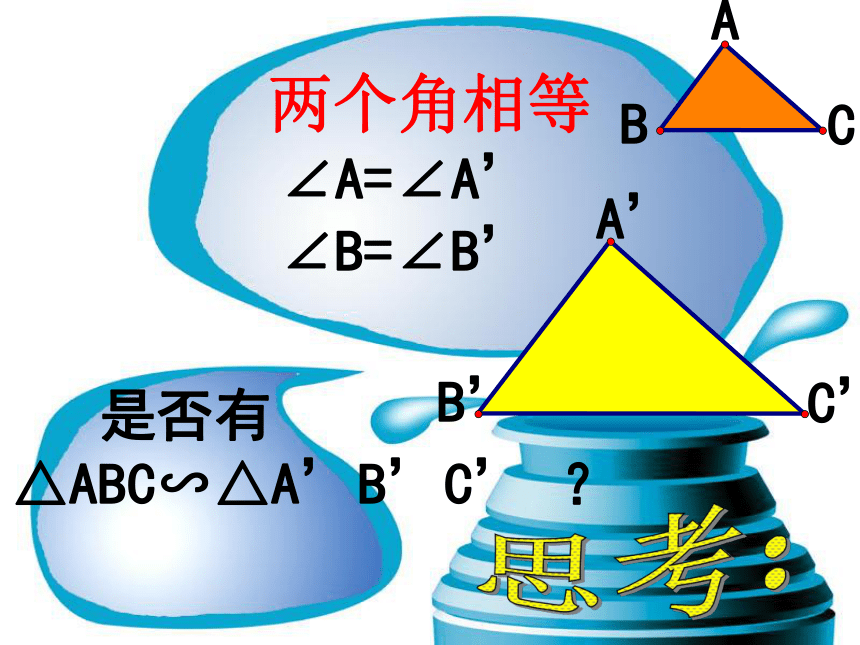
∴△ABC∽△A’B’C’
⑵三对应边的比相等,两三角形相似。
A’
B’
C’
C
B
A
几何符号表示:
∴△ABC∽△A’B’C’
⑶两对应边的比相等,且夹角相等,
两三角形相似。
且∠B=∠B’
有没有其他 办法判断两个 三角形相似?
注意:①对应角、 对应边的书写顺序要与三角形的顺序保持一致。
②强调对应顶点要写 在对应位置。
分组完成的剪纸活动,组里每人剪一个△ABC,满足:
①∠A=600,∠B=500;
②∠A=600,∠B=200;
③∠A=600,∠B=300.
A’
B’
C’
C
B
A
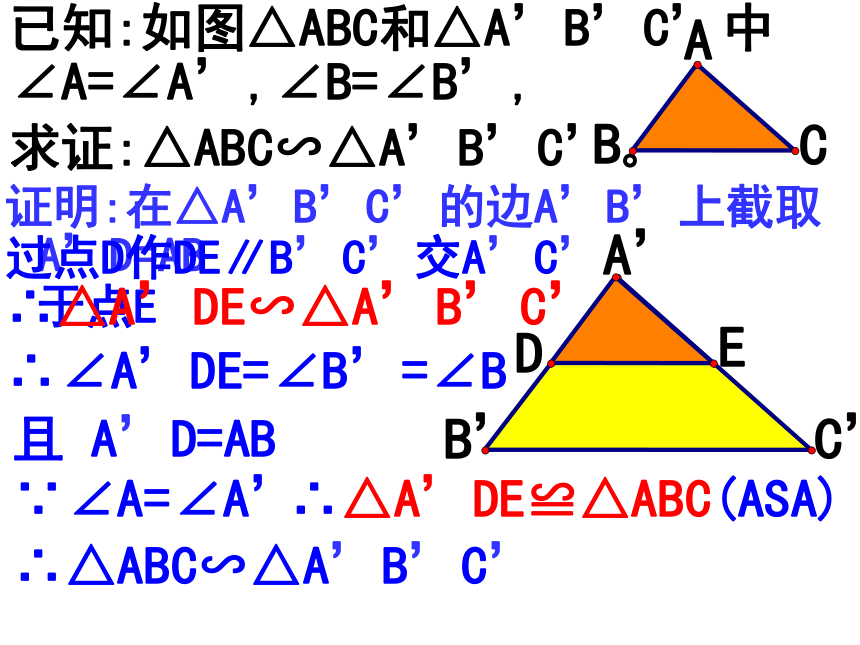
两个角相等
是否有
△ABC∽△A’B’C’ ?
∠A=∠A’
∠B=∠B’
A’
B’
C’
证明:在△A’B’C’的边A’B’上截取A’D=AB
过点D作DE∥B’C’交A’C’于点E
∴△A’DE∽△A’B’C’
∴△ABC∽△A’B’C’
已知:如图△ABC和△A’B’C’中 ∠A=∠A’,∠B=∠B’,
求证:△ABC∽△A’B’C’。
C
B
A
E
D
且 A’D=AB
∵∠A=∠A’
∴△A’DE≌△ABC(ASA)
∴∠A’DE=∠B’=∠B
∴△A’B’C’∽△ABC
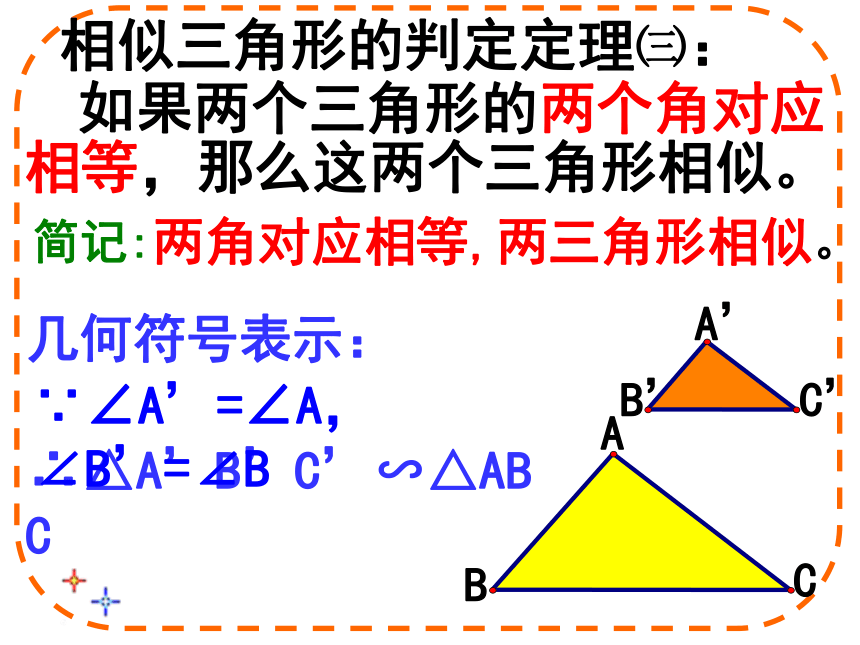
如果两个三角形的两个角对应相等,那么这两个三角形相似。
简记:两角对应相等,两三角形相似。
相似三角形的判定定理㈢:
A
B
C
C’
B’
A’
几何符号表示:
∵∠A’=∠A,∠B’=∠B
一个角对应相等的两个三角形一定相似吗?
例1:已知:在△ABC和△DEF中,∠C=∠E=90?,∠B=∠F,判断△ABC与△DEF相似吗?
解:相似
∵∠C=∠E=90?
∠B=∠F
∴△ABC∽△ ,
( ) ?
两角对应相等,两三角形相似
DFE
70?
在△ABC和△DEF中,
∠A=∠D= ,∠B=60?,∠F=50?,这两个三角形相似吗?为什么?
只要找出两组对应角相等即可。
90?
如图:∠B=∠C,∠ =∠ , 则△_____∽△______。
ABD
ACE
∠B=∠C
寻找条件时,注意利用公共角和对顶角。
A
A
变式:如图,∠1=∠2,要△ABD∽△ACE, 可以补充的一个条件是 。
O
A
B
D
C
E
1
2
3
4
例2:弦AB和CD相交于⊙O内一点P,求证:PA·PB=PC·PD。
A
B
C
D
P
O
证明:连接AC、BD
∵∠A、∠D都是CB所对的圆周角
⌒
∴∠A=∠D
同理:∠C=∠B
∴△PAC∽△PDB
即PA·PB=PC·PD
A
B
C
D
E
已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°, ∠C=85°,∠AED=60°, 求证:AD·AB=AE·AC。
方法4:两角对应相等。
课堂小结:
(这可是今天新学的,要牢记噢!)
方法1:平行于三角形一边的直线。
方法2:三对应边的比相等。
方法3:两对应边的比相等且夹角相等。
相似三角形的判定方法:
A
B
D
C
1.如图,点D在AB上,当 ∠ =∠ 时,△ACD∽△ABC。
ACD
B
(或者∠ACB=∠ADB)
2.已知△ABC中,点E在AC上,点D在AB上,则满足条件 ,就 可以使△ADE与原△ABC相似。
DE//BC
D
(∠C=∠ADE)
(或者∠B=∠ADE)
D
A
B
C
E
●
解:∵∠A=∠A,∠ABD=∠C
∴△ABD∽△ACB
∴AB:AC=AD:AB
∴AB2=AD·AC=2×8=16
∴AB=4
3.已知如图,∠ABD=∠C,AD=2,AC=8,求AB。
A
B
C
D
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
O
C
D
A
B
A
B
C
D
E
不经历风雨,怎么见彩虹
没有人能随随便便成功!
在Rt△ABC的斜边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并说明理由。
思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条?
∴△ADE∽△ABC
⑴平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
D
E
A
B
C
A
B
C
D
E
几何符号表示:
相似三角形的判定:
∴△ABC∽△A’B’C’
⑵三对应边的比相等,两三角形相似。
A’
B’
C’
C
B
A
几何符号表示:
∴△ABC∽△A’B’C’
⑶两对应边的比相等,且夹角相等,
两三角形相似。
且∠B=∠B’
有没有其他 办法判断两个 三角形相似?
注意:①对应角、 对应边的书写顺序要与三角形的顺序保持一致。
②强调对应顶点要写 在对应位置。
分组完成的剪纸活动,组里每人剪一个△ABC,满足:
①∠A=600,∠B=500;
②∠A=600,∠B=200;
③∠A=600,∠B=300.
A’
B’
C’
C
B
A
两个角相等
是否有
△ABC∽△A’B’C’ ?
∠A=∠A’
∠B=∠B’
A’
B’
C’
证明:在△A’B’C’的边A’B’上截取A’D=AB
过点D作DE∥B’C’交A’C’于点E
∴△A’DE∽△A’B’C’
∴△ABC∽△A’B’C’
已知:如图△ABC和△A’B’C’中 ∠A=∠A’,∠B=∠B’,
求证:△ABC∽△A’B’C’。
C
B
A
E
D
且 A’D=AB
∵∠A=∠A’
∴△A’DE≌△ABC(ASA)
∴∠A’DE=∠B’=∠B
∴△A’B’C’∽△ABC
如果两个三角形的两个角对应相等,那么这两个三角形相似。
简记:两角对应相等,两三角形相似。
相似三角形的判定定理㈢:
A
B
C
C’
B’
A’
几何符号表示:
∵∠A’=∠A,∠B’=∠B
一个角对应相等的两个三角形一定相似吗?
例1:已知:在△ABC和△DEF中,∠C=∠E=90?,∠B=∠F,判断△ABC与△DEF相似吗?
解:相似
∵∠C=∠E=90?
∠B=∠F
∴△ABC∽△ ,
( ) ?
两角对应相等,两三角形相似
DFE
70?
在△ABC和△DEF中,
∠A=∠D= ,∠B=60?,∠F=50?,这两个三角形相似吗?为什么?
只要找出两组对应角相等即可。
90?
如图:∠B=∠C,∠ =∠ , 则△_____∽△______。
ABD
ACE
∠B=∠C
寻找条件时,注意利用公共角和对顶角。
A
A
变式:如图,∠1=∠2,要△ABD∽△ACE, 可以补充的一个条件是 。
O
A
B
D
C
E
1
2
3
4
例2:弦AB和CD相交于⊙O内一点P,求证:PA·PB=PC·PD。
A
B
C
D
P
O
证明:连接AC、BD
∵∠A、∠D都是CB所对的圆周角
⌒
∴∠A=∠D
同理:∠C=∠B
∴△PAC∽△PDB
即PA·PB=PC·PD
A
B
C
D
E
已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°, ∠C=85°,∠AED=60°, 求证:AD·AB=AE·AC。
方法4:两角对应相等。
课堂小结:
(这可是今天新学的,要牢记噢!)
方法1:平行于三角形一边的直线。
方法2:三对应边的比相等。
方法3:两对应边的比相等且夹角相等。
相似三角形的判定方法:
A
B
D
C
1.如图,点D在AB上,当 ∠ =∠ 时,△ACD∽△ABC。
ACD
B
(或者∠ACB=∠ADB)
2.已知△ABC中,点E在AC上,点D在AB上,则满足条件 ,就 可以使△ADE与原△ABC相似。
DE//BC
D
(∠C=∠ADE)
(或者∠B=∠ADE)
D
A
B
C
E
●
解:∵∠A=∠A,∠ABD=∠C
∴△ABD∽△ACB
∴AB:AC=AD:AB
∴AB2=AD·AC=2×8=16
∴AB=4
3.已知如图,∠ABD=∠C,AD=2,AC=8,求AB。
A
B
C
D
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
O
C
D
A
B
A
B
C
D
E
不经历风雨,怎么见彩虹
没有人能随随便便成功!
在Rt△ABC的斜边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并说明理由。
思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条?
