28.2.1 解直角三角形 复习课件(共17张PPT)
文档属性
| 名称 | 28.2.1 解直角三角形 复习课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 767.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览




文档简介
解直角三角形
1、理解并掌握锐角三角函数定义和性质;
2、熟记特殊角的三角函数值;
3、理解并掌握解直角三角形的基本知识,熟悉直角三角形中的边角关系,具有构造直角三角形解决问题的意识和能力。
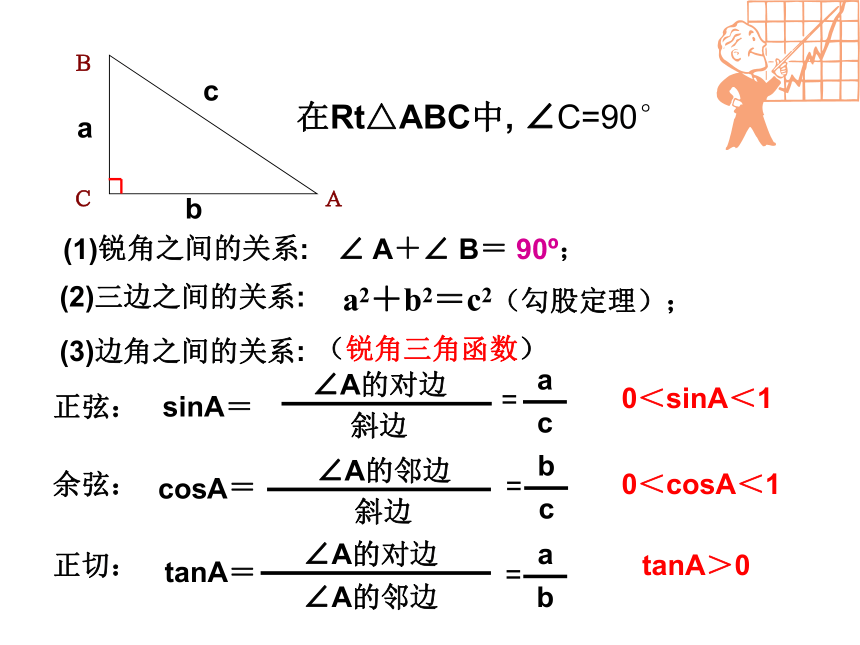
解直角三角形
(2)三边之间的关系:
a2+b2=c2(勾股定理);
(1)锐角之间的关系:
∠ A+∠ B= 90?;
(3)边角之间的关系:
sinA=
cosA=
tanA=
B
A
C
a
b
c
∠A的对边
斜边
a
c
=
a
b
=
b
c
=
∠A的邻边
斜边
∠A的对边
∠A的邻边
在Rt△ABC中, ∠C=90°
正弦:
余弦:
正切:
(锐角三角函数)
0<sinA<1
0<cosA<1
tanA>0
30°
45°
60°
sinα
cosα
tanα
角α
三角函数
2
2
2
1
3
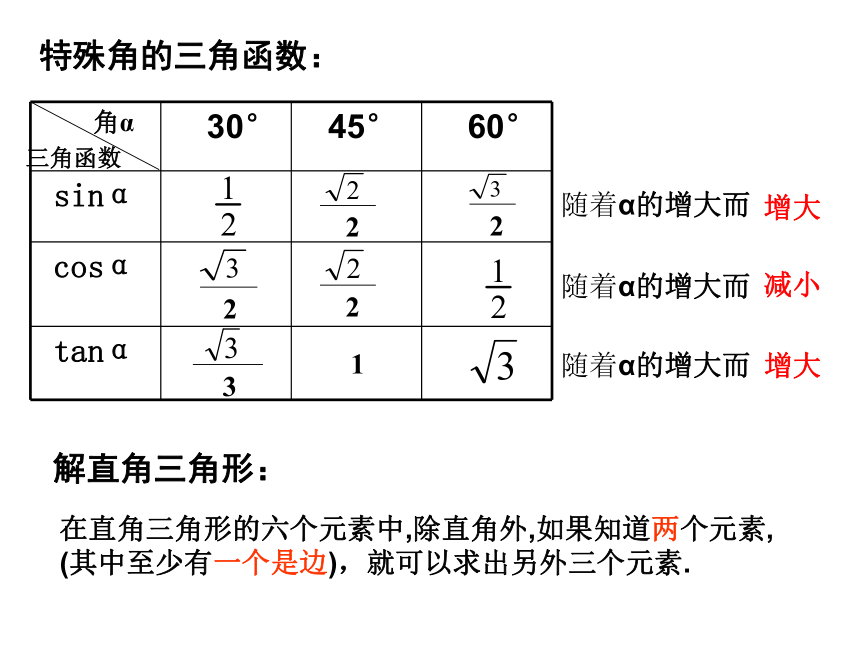
特殊角的三角函数:
2
随着α的增大而
随着α的增大而
随着α的增大而
在直角三角形的六个元素中,除直角外,如果知道两个元素,
(其中至少有一个是边),就可以求出另外三个元素.
解直角三角形:
增大
增大
减小
在Rt△ABC中, ∠C=90 °
(1)若AC = 4 , BC = 3 ,
①AB=__________;
②sinA=( ), cosA=( ),tanA=( )。
(2)①若∠A= 30°, 斜边AB = 20 ,则AC=_____;
②若AC= ,BC= ,则∠B=_____。
③若sinA= ,AC= ,那么BC的值为______。
5
60°
3
5
4
20
30°
?
?
√6
√2
?
sinA=
√2
2
2√2
例1:
= ×(2× — )+ ×
解:原式
跟踪练习:
2.
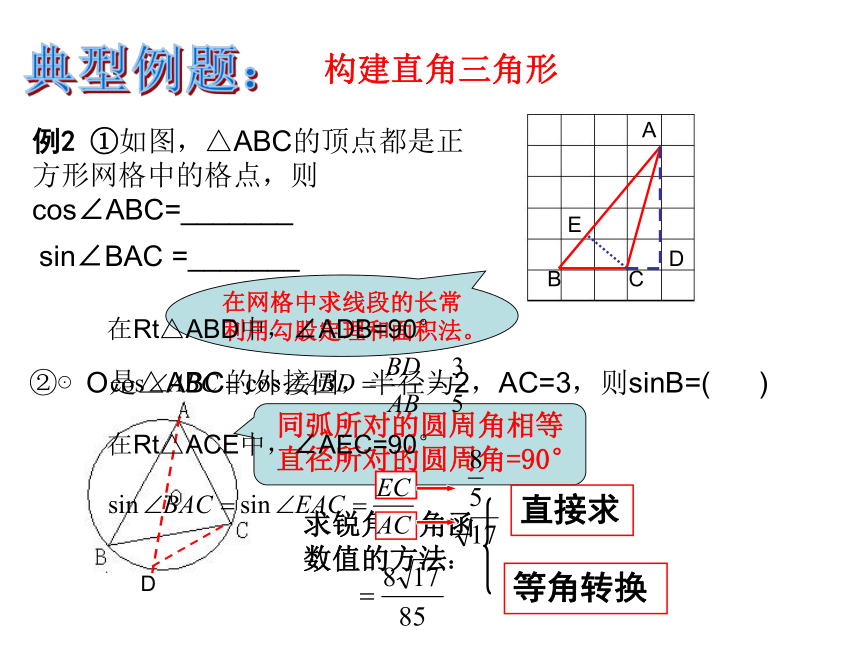
例2 ①如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC=_______
C
B
A
sin∠BAC =_______
E
D
构建直角三角形
②⊙O是△ABC的外接圆,半径为2,AC=3,则sinB=( )
在网格中求线段的长常利用勾股定理和面积法。
D
直径所对的圆周角=90°
同弧所对的圆周角相等
求锐角三角函数值的方法:
直接求
等角转换
在Rt△ABD中,∠ADB=90°
在Rt△ACE中,∠AEC=90°
跟踪练习1:
如图,△ABC中,
∠A=30°,∠C=105°,
若BC=2,求AB的长。
D
2
如图,已知直线 ,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,
则 = .
跟踪练习2:
例3 为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务.某天我护航舰正在某小岛A北偏西45°并距该岛20海里的B处待命.位于该岛正西方向C处的某外国商船遭到海盗袭击,船长发现在其北偏东60°的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿BC航线以每小时60海里的速度前去救援.问我护航舰需多少分钟
可以到达该商船所在的位置C处?
(结果精确到个位.参考数据:
≈1.4, ≈1.7)
【解析】由图可知,∠ACB=30°,∠BAC=45°,
作BD⊥AC于D(如图),在Rt△ADB中,
AB=20,∴BD=ABsin 45°=20× =10 .
在Rt△BDC中,∠DCB=30°
∴BC=2×10 =20 ≈28,
∴ ≈0.47,
∴0.47×60=28.2≈28(分钟).
答:我护航舰约需28分钟就可到达该商船所在的位置C处.
请你谈谈对本节学习内容的体会和感受。
今天你有什么收获?
1、已知:在Rt△ABC中,∠C=90°,sinA= ,则cosA=_______。
2、矩形ABCD中AB=10,BC=8, E为AD边上一点,沿BE将△BDE翻折,点D正好落在AB边上,求 tan∠AFE.
3、如图,以△ABC的一边AB为直径作⊙O, ⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E。(1)求证:DE⊥AC;
(2)若∠ABC=30°,求tan∠BCO的值。
1、理解并掌握锐角三角函数定义和性质;
2、熟记特殊角的三角函数值;
3、理解并掌握解直角三角形的基本知识,熟悉直角三角形中的边角关系,具有构造直角三角形解决问题的意识和能力。
解直角三角形
(2)三边之间的关系:
a2+b2=c2(勾股定理);
(1)锐角之间的关系:
∠ A+∠ B= 90?;
(3)边角之间的关系:
sinA=
cosA=
tanA=
B
A
C
a
b
c
∠A的对边
斜边
a
c
=
a
b
=
b
c
=
∠A的邻边
斜边
∠A的对边
∠A的邻边
在Rt△ABC中, ∠C=90°
正弦:
余弦:
正切:
(锐角三角函数)
0<sinA<1
0<cosA<1
tanA>0
30°
45°
60°
sinα
cosα
tanα
角α
三角函数
2
2
2
1
3
特殊角的三角函数:
2
随着α的增大而
随着α的增大而
随着α的增大而
在直角三角形的六个元素中,除直角外,如果知道两个元素,
(其中至少有一个是边),就可以求出另外三个元素.
解直角三角形:
增大
增大
减小
在Rt△ABC中, ∠C=90 °
(1)若AC = 4 , BC = 3 ,
①AB=__________;
②sinA=( ), cosA=( ),tanA=( )。
(2)①若∠A= 30°, 斜边AB = 20 ,则AC=_____;
②若AC= ,BC= ,则∠B=_____。
③若sinA= ,AC= ,那么BC的值为______。
5
60°
3
5
4
20
30°
?
?
√6
√2
?
sinA=
√2
2
2√2
例1:
= ×(2× — )+ ×
解:原式
跟踪练习:
2.
例2 ①如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC=_______
C
B
A
sin∠BAC =_______
E
D
构建直角三角形
②⊙O是△ABC的外接圆,半径为2,AC=3,则sinB=( )
在网格中求线段的长常利用勾股定理和面积法。
D
直径所对的圆周角=90°
同弧所对的圆周角相等
求锐角三角函数值的方法:
直接求
等角转换
在Rt△ABD中,∠ADB=90°
在Rt△ACE中,∠AEC=90°
跟踪练习1:
如图,△ABC中,
∠A=30°,∠C=105°,
若BC=2,求AB的长。
D
2
如图,已知直线 ,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,
则 = .
跟踪练习2:
例3 为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务.某天我护航舰正在某小岛A北偏西45°并距该岛20海里的B处待命.位于该岛正西方向C处的某外国商船遭到海盗袭击,船长发现在其北偏东60°的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿BC航线以每小时60海里的速度前去救援.问我护航舰需多少分钟
可以到达该商船所在的位置C处?
(结果精确到个位.参考数据:
≈1.4, ≈1.7)
【解析】由图可知,∠ACB=30°,∠BAC=45°,
作BD⊥AC于D(如图),在Rt△ADB中,
AB=20,∴BD=ABsin 45°=20× =10 .
在Rt△BDC中,∠DCB=30°
∴BC=2×10 =20 ≈28,
∴ ≈0.47,
∴0.47×60=28.2≈28(分钟).
答:我护航舰约需28分钟就可到达该商船所在的位置C处.
请你谈谈对本节学习内容的体会和感受。
今天你有什么收获?
1、已知:在Rt△ABC中,∠C=90°,sinA= ,则cosA=_______。
2、矩形ABCD中AB=10,BC=8, E为AD边上一点,沿BE将△BDE翻折,点D正好落在AB边上,求 tan∠AFE.
3、如图,以△ABC的一边AB为直径作⊙O, ⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E。(1)求证:DE⊥AC;
(2)若∠ABC=30°,求tan∠BCO的值。
