鲁教版(五四制)数学六年级数学上册2.7有理数乘法 课件(19张)
文档属性
| 名称 | 鲁教版(五四制)数学六年级数学上册2.7有理数乘法 课件(19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览





文档简介
有理数的乘法(一)
学习目标
知识目标:使学生在了解有理数乘法的意义 的基础上,掌握有理数乘法法则。
能力目标:初步掌握有理数乘法法则的合理 性,培养学生观察、归纳、概括及运算的能力。
情感目标:在传授知识、培养能力的同时,注意培养学生勇于探索的精神。
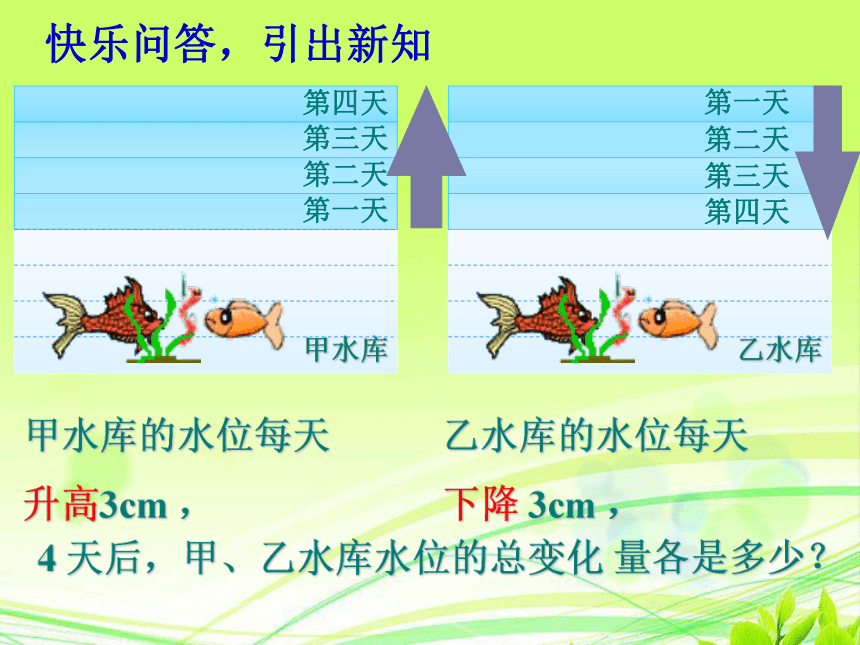
甲水库
第一天
乙水库
甲水库的水位每天
升高3cm ,
第二天
第三天
第四天
乙水库的水位每天
下降 3cm ,
第一天
第二天
第三天
第四天
4 天后,甲、乙水库水位的总变化 量各是多少?
快乐问答,引出新知
甲水库
第一天
乙水库
第二天
第三天
第四天
第一天
第二天
第三天
第四天
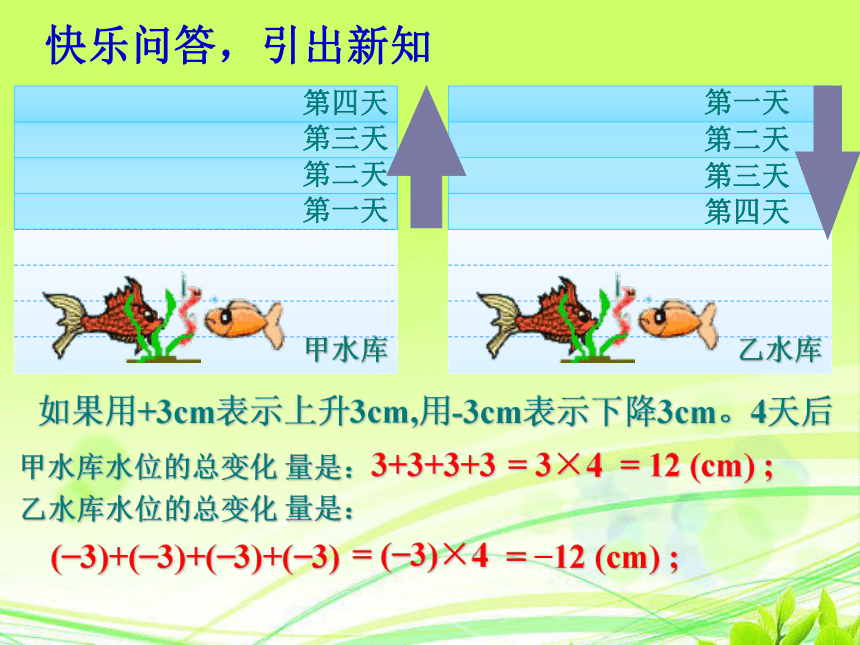
如果用+3cm表示上升3cm,用-3cm表示下降3cm。4天后
甲水库水位的总变化 量是:
乙水库水位的总变化 量是:
3+3+3+3
(?3)+(?3)+(?3)+(?3)
快乐问答,引出新知
= 3×4
= 12 (cm) ;
= ?12 (cm) ;
= (?3)×4
(?3)×4 = ?12
(?3)×3 = ,
(?3)×2 = ,
(?3)×1 = ,
(?3)×0 = ,
?9
?6
?3
0
(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,
第二个因数减少 1 时,积 怎么变化?
3
6
9
12
当第二个因数从 0 减少为 ?1时,
积从 增大为____
积增大 3 。
0
3
猜 一 猜
?
齐心协力,探究新知
(?3)×4 = ?12
(?3)×3 = ,
(?3)×2 = ,
(?3)×1 = ,
(?3)×0 = ,
?9
?6
?3
0
(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,
3
6
9
12
你能看出两有理数相乘与它们的积之间的规律吗?
归纳 ?
(1)积的符号
正数乘以正数得---
负数乘负数得-----
(3)一个数同0相乘 得 ---
(2)积的绝对值
绝对值-----
试用简练的语言叙述上面得出的结论。
齐心协力,探究新知
负数乘正数得----,
有理数的乘法法则
两数相乘,同号得 ,异号得 ,
绝对值相乘;
任何数同0相乘,积仍为0.
正
负
怎样利用法则来进行两有理数的乘法运算与得出结果的?
齐心协力,探究新知
例题解析 巩固提高
例1 计算:
(1) (?4)×5 ; (2) (?4)×(?7) ;
(3) (4)
=1 ;
=1 ;
计算两数相乘第一步是 ;
确定积的符号
第二步
是 ;
绝对值相乘
解:(1) (?4)×5
=?20 ;
(2) (?4)×(?7)
=?( )
=+(4×7)
=28;
(3)
(4)
4×5
倒 数 的 定 义
由例 1 的 (3) (4)
? 解题后的反思 ?
(3) (4)
=1;
=1 ;
可知
三个有理数相乘,你会计算吗?
例 题 解 析
例2 计算:
(1) (?4)×5×(?0.25); (2)
解:(1) (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25)
=+(20×0.25)
=5.
=(?20)×(?0.25)
方法提示
三个有理数相乘,先把前两个相乘,
再把
所得结果与另一数相乘。
例2 计算:
(1) (?4)×5×(?0.25); (2)
解:(1) (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25)
=+(20×0.25)
=5.
=(?20)×(?0.25)
(2)
=?1 .
拓展提高,灵活运用
多个有理数相乘, 积的符号怎样确定?
与负因数的个数有什么关系?
确定下列积的符号,你能发现什么?
1)(-2)×3×4×5
2) (-2)×(-3)×4×5
3) (-2)×(-3)×(-4)×5
4)(-2)×(-3)×(-4)×(-5)
5)(-2)×(-3)×4×5×0
? 解题后的反思 ?
积的符号与负因数
的个数有什么关系?
解:(1) (?4)×5 ×(?0.25) (2)
= =
几个不等于零的有理数相乘, 积的符号由负因数的个数确定。
积的绝对值怎样确定?
-( )
有一因数为 0 时,积是多少?
? 解题后的反思 ?
4×5×0.25
+( )
几个不等于0的有理数相乘,
积的符号由 来决定:
负因数的个数
负因数个数是奇数时积为负,
积的绝对值等于各个因数绝对值的
积。
归纳总结
负因数个数是偶数时积为正。
几个数相乘有一因数为 0 时,积就为
0
(1)
( 8)
×
( 7)
(2)
2.9
×
( 0.4)
(3)(- )
×
8
9
1
4
(4)
100
×
( 0.001)
(5)
×
3
( 2)
×
( 4)
(6)
×
(-7)
( 6)
×
( 5)
巩固练习 升华提高
看看谁算得快
看谁算得快
看谁说得快
用“>” “<”或“=”号填空:
1﹑如果 a<0, b>0, 那么ab( )0;
2﹑如果 a>0, b<0, 那么ab( )0;
3﹑如果 a<0, b<0, 那么ab( )0;
4﹑如果 a>0, b>0, 那么ab( )0;
5﹑如果 a = 0, b≠0, 那么ab( )0.
<
<
>
>
=
1、两个有理数相乘的法则是....?
2、倒数的定义?
3、几个有理数相乘的法则是....?
4、计算有理数乘法的第一步.....,第二步.....
归纳小结,反思提高
当堂检测 知识反馈
1)(-8)x1.25
2) (-5)x(-12)
3) 7.5x(-8.2)x0x(-1.92)
4) 5x(-20)x(-3.1)x(-2)
课后作业(必做)
课本53 习题2.10 第1题
拓展作业(选做)
伴你学2.10第2题
学习目标
知识目标:使学生在了解有理数乘法的意义 的基础上,掌握有理数乘法法则。
能力目标:初步掌握有理数乘法法则的合理 性,培养学生观察、归纳、概括及运算的能力。
情感目标:在传授知识、培养能力的同时,注意培养学生勇于探索的精神。
甲水库
第一天
乙水库
甲水库的水位每天
升高3cm ,
第二天
第三天
第四天
乙水库的水位每天
下降 3cm ,
第一天
第二天
第三天
第四天
4 天后,甲、乙水库水位的总变化 量各是多少?
快乐问答,引出新知
甲水库
第一天
乙水库
第二天
第三天
第四天
第一天
第二天
第三天
第四天
如果用+3cm表示上升3cm,用-3cm表示下降3cm。4天后
甲水库水位的总变化 量是:
乙水库水位的总变化 量是:
3+3+3+3
(?3)+(?3)+(?3)+(?3)
快乐问答,引出新知
= 3×4
= 12 (cm) ;
= ?12 (cm) ;
= (?3)×4
(?3)×4 = ?12
(?3)×3 = ,
(?3)×2 = ,
(?3)×1 = ,
(?3)×0 = ,
?9
?6
?3
0
(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,
第二个因数减少 1 时,积 怎么变化?
3
6
9
12
当第二个因数从 0 减少为 ?1时,
积从 增大为____
积增大 3 。
0
3
猜 一 猜
?
齐心协力,探究新知
(?3)×4 = ?12
(?3)×3 = ,
(?3)×2 = ,
(?3)×1 = ,
(?3)×0 = ,
?9
?6
?3
0
(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,
3
6
9
12
你能看出两有理数相乘与它们的积之间的规律吗?
归纳 ?
(1)积的符号
正数乘以正数得---
负数乘负数得-----
(3)一个数同0相乘 得 ---
(2)积的绝对值
绝对值-----
试用简练的语言叙述上面得出的结论。
齐心协力,探究新知
负数乘正数得----,
有理数的乘法法则
两数相乘,同号得 ,异号得 ,
绝对值相乘;
任何数同0相乘,积仍为0.
正
负
怎样利用法则来进行两有理数的乘法运算与得出结果的?
齐心协力,探究新知
例题解析 巩固提高
例1 计算:
(1) (?4)×5 ; (2) (?4)×(?7) ;
(3) (4)
=1 ;
=1 ;
计算两数相乘第一步是 ;
确定积的符号
第二步
是 ;
绝对值相乘
解:(1) (?4)×5
=?20 ;
(2) (?4)×(?7)
=?( )
=+(4×7)
=28;
(3)
(4)
4×5
倒 数 的 定 义
由例 1 的 (3) (4)
? 解题后的反思 ?
(3) (4)
=1;
=1 ;
可知
三个有理数相乘,你会计算吗?
例 题 解 析
例2 计算:
(1) (?4)×5×(?0.25); (2)
解:(1) (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25)
=+(20×0.25)
=5.
=(?20)×(?0.25)
方法提示
三个有理数相乘,先把前两个相乘,
再把
所得结果与另一数相乘。
例2 计算:
(1) (?4)×5×(?0.25); (2)
解:(1) (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25)
=+(20×0.25)
=5.
=(?20)×(?0.25)
(2)
=?1 .
拓展提高,灵活运用
多个有理数相乘, 积的符号怎样确定?
与负因数的个数有什么关系?
确定下列积的符号,你能发现什么?
1)(-2)×3×4×5
2) (-2)×(-3)×4×5
3) (-2)×(-3)×(-4)×5
4)(-2)×(-3)×(-4)×(-5)
5)(-2)×(-3)×4×5×0
? 解题后的反思 ?
积的符号与负因数
的个数有什么关系?
解:(1) (?4)×5 ×(?0.25) (2)
= =
几个不等于零的有理数相乘, 积的符号由负因数的个数确定。
积的绝对值怎样确定?
-( )
有一因数为 0 时,积是多少?
? 解题后的反思 ?
4×5×0.25
+( )
几个不等于0的有理数相乘,
积的符号由 来决定:
负因数的个数
负因数个数是奇数时积为负,
积的绝对值等于各个因数绝对值的
积。
归纳总结
负因数个数是偶数时积为正。
几个数相乘有一因数为 0 时,积就为
0
(1)
( 8)
×
( 7)
(2)
2.9
×
( 0.4)
(3)(- )
×
8
9
1
4
(4)
100
×
( 0.001)
(5)
×
3
( 2)
×
( 4)
(6)
×
(-7)
( 6)
×
( 5)
巩固练习 升华提高
看看谁算得快
看谁算得快
看谁说得快
用“>” “<”或“=”号填空:
1﹑如果 a<0, b>0, 那么ab( )0;
2﹑如果 a>0, b<0, 那么ab( )0;
3﹑如果 a<0, b<0, 那么ab( )0;
4﹑如果 a>0, b>0, 那么ab( )0;
5﹑如果 a = 0, b≠0, 那么ab( )0.
<
<
>
>
=
1、两个有理数相乘的法则是....?
2、倒数的定义?
3、几个有理数相乘的法则是....?
4、计算有理数乘法的第一步.....,第二步.....
归纳小结,反思提高
当堂检测 知识反馈
1)(-8)x1.25
2) (-5)x(-12)
3) 7.5x(-8.2)x0x(-1.92)
4) 5x(-20)x(-3.1)x(-2)
课后作业(必做)
课本53 习题2.10 第1题
拓展作业(选做)
伴你学2.10第2题
