人教版七年级数学下册课件:8.2 第2课时 加减消元法(23张)
文档属性
| 名称 | 人教版七年级数学下册课件:8.2 第2课时 加减消元法(23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览







文档简介
第八章 二元一次方程组
8.2 第2课时 加减消元法
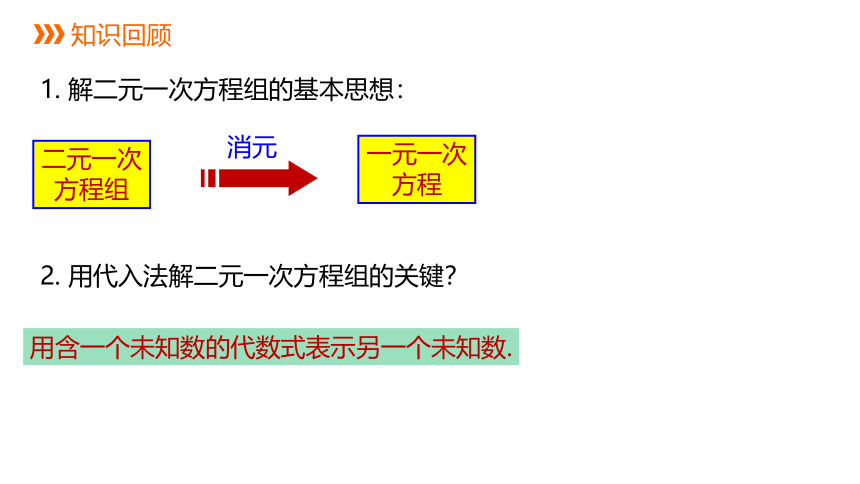
知识回顾
1. 解二元一次方程组的基本思想:
二元一次方程组
一元一次方程
消元
2. 用代入法解二元一次方程组的关键?
用含一个未知数的代数式表示另一个未知数.
写解
回代
代入
把变形后的方程代入到另一个方程中,消去一个元并解一元一次方程
代入变式求得另一个未知数的值
写出方程组的解
变形
用含有一个未知数的代数式表示另一个未知数, 写成y=ax+b或x=ay+b
2、用代入法解方程的步骤是什么?
获取新知
思 考
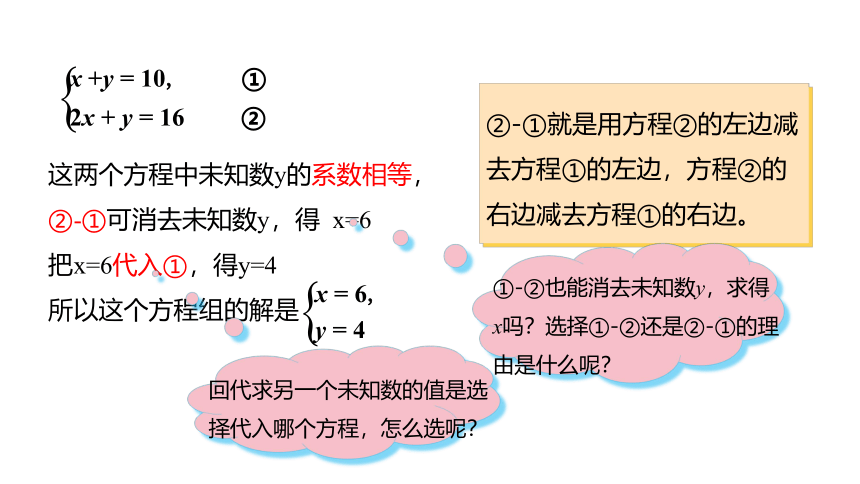
x +y = 10, ①
2x + y = 16 ②
问题1:除了用代入法求解外,还有其他方法吗?
问题2:两个方程中同一未知数的系数有什么特点吗?
这两个方程中未知数y的系数相等,
②-①可消去未知数y,得 x=6
把x=6代入①,得y=4
所以这个方程组的解是
x = 6,
y = 4
x +y = 10, ①
2x + y = 16 ②
②-①就是用方程②的左边减去方程①的左边,方程②的右边减去方程①的右边。
①-②也能消去未知数y,求得
x吗?选择①-②还是②-①的理由是什么呢?
回代求另一个未知数的值是选择代入哪个方程,怎么选呢?
联系上面的解法,想一想怎样解方程组
3x + 10y = 2.8,①
15x - 10y = 8 ,②
未知数y的系数互为相反数,
由①+②,可消去未知数y,
从而求出未知数x的值.
解:①+②,得
18x=10.8,
x=0.6.
把x=0.6代入①,得
3×0.6+10y=2.8,
y=0.1.
所以这个方程组的解是
3x+ 10y+(15x-10y) =2.8 +8,
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,
把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法
例题讲解
例1 用加减法解方程组:
分析:这两个方程中没有同一个未知数的系数相反或相等,直接加减这两个方程不能消元. 我们对方程变形,使得这两个方程中某个未知数的系数相反或相等.
找系数的最小公倍数
解:①×3,得 9x+12y=48. ③
②×2,得 10x-12y=66. ④
③+④,得19x=114,
即 x=6.
把x=6代入① ,得 3×6+4y=16,
4y= -2,
y=
所以这个方程组的解是
在加减消元时,
具体选择消去谁,
回代入哪个方程,
主要取决于怎么做简便
用加减消元法解二元一次方程组时,一般有三种情况:
①方程组中某个未知数的系数的绝对值相等,则直接利用加减法求解;
②方程组中任一个未知数的系数的绝对值都不相等,但某个未知数的系数的绝对值成倍数关系,则其中一个方程乘这个倍数后再利用加减法求解;
③方程组中任一个未知数的系数的绝对值既不相等,也不成倍数关系,可利用最小公倍数的知识,把两个方程都适当地乘一个数,使某个未知数的系数的绝对值相等,然后再利用加减法求解.
例2 2台大收割机和5台小收割机同时工作2 h共收割小麦3. 6 hm2, 3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2. 1台大收割机和1台小收割机每小时各收割小麦多少公顷?
分析:如果1台大收割机和1台小收割机每小时各收割小麦x hm2和y hm2, 那么2台大收割机和5台小收割机同时工作1 h共收割小麦_________ hm2,3台大收割机和2台小收割机同时工作1 h共收割小麦________hm2. 由此考虑两种情况下的工作量.
(2x + 5y)
(3x + 2y)
解:设1台大收割机和1台小收割机每小时各收割小麦x hm2和y hm2. 根据两种工作方式中的相等关系,
得方程组
去括号,得
②-①,得11x=4.4.
解这个方程,得x=0.4.
把x=0.4代入①,得y=0.2.
因此,这个方程组的解是
答:1台大收割机和1台小收割机每小时各收割小麦0. 4 hm2和0. 2 hm2 上面
上面解方程组的过程可以用下面的框图表示:
二元一次方程组
一元一次方程
11x=4.4
x=0.4
代入
解得
两方程相减,消去未知数y
4x+10y=3.6,①
15x+10y=8,②
②-①
y=0.2
随堂演练
1. 用加减法解方程组 应用( )
A.①-②消去y B.①-②消去x
C. ②- ①消去常数项 D. 以上都不对
6x+7y=-19,①
6x-5y=17②
B
2. 解方程组 时,用加减消元法最简便的是( )
A.①+②
B.①-②
C.①×2-②×3
D.①×3+②×2
A
3. 用加减法解方程组 时,要使两个方程中同一未知数的系数相等或相反,有以下四种变形的结果:
其中变形正确的是( )
A.①② B.③④ C.①③ D.②④
B
4. 方程组 中,x的系数的特点是_____,
方程组 中,y的系数的特点是____________,这两个方程组用________消元法解较简便.
相等
互为相反数
加减
5.解方程组:
解(1):①+②,得6x=12,
解得x=2.把x=2
代入②,得3×2+7y=13,解得y=1.
所以原方程组的解为
(2)①+②,得4x=8,
解这个方程,得x=2.
把x=2代入①,得y= .
因此,这个方程组的解是
(3)①×2,得10x+4y=50.③
③-②,得7x=35,解这个方程,得x=5.
把x=5代入①,得5×5+2y=25,y=0.
因此,这个方程组的解是
(4)①×3,得6x+15y=24.③
②×2,得6x+4y=10.④
③-④,得11y=14,y= .
把y= 代入①,得2x+5× =8,x= .
因此,这个方程组的解是
6. 为了响应“足球进校园”的号召,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元. (1)求A,B两种品牌的足球的单价; (2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
解得
解:(1)设A品牌的足球的单价为x元/个,B品牌的足球
的单价为y元/个,依题意得
答:A品牌的足球的单价为40元/个,B品牌的足球的单价100元/个.
(2)依题意得20×40+2×100=1000(元).
答:该校购买20个A品牌的足球和2个B品牌的足球的总费用是1000元.
课堂小结
解二元一次方程组
基本思路“消元”
加减法解二元一次方程组的一般步骤
变形:取绝对值较小的未知数(同一个未知数)的系数的最小公倍数,用适当的数去乘方程的两边
消元:当未知数的系数相等时,将两个方程相减;当未知数的系数互为相反数时,将两个方程相加
求解:解消元后得到的一元一次方程
写:写出方程组的解
回代:把求得的未知数的值代入方程组中某个较简单的方程中
8.2 第2课时 加减消元法
知识回顾
1. 解二元一次方程组的基本思想:
二元一次方程组
一元一次方程
消元
2. 用代入法解二元一次方程组的关键?
用含一个未知数的代数式表示另一个未知数.
写解
回代
代入
把变形后的方程代入到另一个方程中,消去一个元并解一元一次方程
代入变式求得另一个未知数的值
写出方程组的解
变形
用含有一个未知数的代数式表示另一个未知数, 写成y=ax+b或x=ay+b
2、用代入法解方程的步骤是什么?
获取新知
思 考
x +y = 10, ①
2x + y = 16 ②
问题1:除了用代入法求解外,还有其他方法吗?
问题2:两个方程中同一未知数的系数有什么特点吗?
这两个方程中未知数y的系数相等,
②-①可消去未知数y,得 x=6
把x=6代入①,得y=4
所以这个方程组的解是
x = 6,
y = 4
x +y = 10, ①
2x + y = 16 ②
②-①就是用方程②的左边减去方程①的左边,方程②的右边减去方程①的右边。
①-②也能消去未知数y,求得
x吗?选择①-②还是②-①的理由是什么呢?
回代求另一个未知数的值是选择代入哪个方程,怎么选呢?
联系上面的解法,想一想怎样解方程组
3x + 10y = 2.8,①
15x - 10y = 8 ,②
未知数y的系数互为相反数,
由①+②,可消去未知数y,
从而求出未知数x的值.
解:①+②,得
18x=10.8,
x=0.6.
把x=0.6代入①,得
3×0.6+10y=2.8,
y=0.1.
所以这个方程组的解是
3x+ 10y+(15x-10y) =2.8 +8,
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,
把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法
例题讲解
例1 用加减法解方程组:
分析:这两个方程中没有同一个未知数的系数相反或相等,直接加减这两个方程不能消元. 我们对方程变形,使得这两个方程中某个未知数的系数相反或相等.
找系数的最小公倍数
解:①×3,得 9x+12y=48. ③
②×2,得 10x-12y=66. ④
③+④,得19x=114,
即 x=6.
把x=6代入① ,得 3×6+4y=16,
4y= -2,
y=
所以这个方程组的解是
在加减消元时,
具体选择消去谁,
回代入哪个方程,
主要取决于怎么做简便
用加减消元法解二元一次方程组时,一般有三种情况:
①方程组中某个未知数的系数的绝对值相等,则直接利用加减法求解;
②方程组中任一个未知数的系数的绝对值都不相等,但某个未知数的系数的绝对值成倍数关系,则其中一个方程乘这个倍数后再利用加减法求解;
③方程组中任一个未知数的系数的绝对值既不相等,也不成倍数关系,可利用最小公倍数的知识,把两个方程都适当地乘一个数,使某个未知数的系数的绝对值相等,然后再利用加减法求解.
例2 2台大收割机和5台小收割机同时工作2 h共收割小麦3. 6 hm2, 3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2. 1台大收割机和1台小收割机每小时各收割小麦多少公顷?
分析:如果1台大收割机和1台小收割机每小时各收割小麦x hm2和y hm2, 那么2台大收割机和5台小收割机同时工作1 h共收割小麦_________ hm2,3台大收割机和2台小收割机同时工作1 h共收割小麦________hm2. 由此考虑两种情况下的工作量.
(2x + 5y)
(3x + 2y)
解:设1台大收割机和1台小收割机每小时各收割小麦x hm2和y hm2. 根据两种工作方式中的相等关系,
得方程组
去括号,得
②-①,得11x=4.4.
解这个方程,得x=0.4.
把x=0.4代入①,得y=0.2.
因此,这个方程组的解是
答:1台大收割机和1台小收割机每小时各收割小麦0. 4 hm2和0. 2 hm2 上面
上面解方程组的过程可以用下面的框图表示:
二元一次方程组
一元一次方程
11x=4.4
x=0.4
代入
解得
两方程相减,消去未知数y
4x+10y=3.6,①
15x+10y=8,②
②-①
y=0.2
随堂演练
1. 用加减法解方程组 应用( )
A.①-②消去y B.①-②消去x
C. ②- ①消去常数项 D. 以上都不对
6x+7y=-19,①
6x-5y=17②
B
2. 解方程组 时,用加减消元法最简便的是( )
A.①+②
B.①-②
C.①×2-②×3
D.①×3+②×2
A
3. 用加减法解方程组 时,要使两个方程中同一未知数的系数相等或相反,有以下四种变形的结果:
其中变形正确的是( )
A.①② B.③④ C.①③ D.②④
B
4. 方程组 中,x的系数的特点是_____,
方程组 中,y的系数的特点是____________,这两个方程组用________消元法解较简便.
相等
互为相反数
加减
5.解方程组:
解(1):①+②,得6x=12,
解得x=2.把x=2
代入②,得3×2+7y=13,解得y=1.
所以原方程组的解为
(2)①+②,得4x=8,
解这个方程,得x=2.
把x=2代入①,得y= .
因此,这个方程组的解是
(3)①×2,得10x+4y=50.③
③-②,得7x=35,解这个方程,得x=5.
把x=5代入①,得5×5+2y=25,y=0.
因此,这个方程组的解是
(4)①×3,得6x+15y=24.③
②×2,得6x+4y=10.④
③-④,得11y=14,y= .
把y= 代入①,得2x+5× =8,x= .
因此,这个方程组的解是
6. 为了响应“足球进校园”的号召,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元. (1)求A,B两种品牌的足球的单价; (2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
解得
解:(1)设A品牌的足球的单价为x元/个,B品牌的足球
的单价为y元/个,依题意得
答:A品牌的足球的单价为40元/个,B品牌的足球的单价100元/个.
(2)依题意得20×40+2×100=1000(元).
答:该校购买20个A品牌的足球和2个B品牌的足球的总费用是1000元.
课堂小结
解二元一次方程组
基本思路“消元”
加减法解二元一次方程组的一般步骤
变形:取绝对值较小的未知数(同一个未知数)的系数的最小公倍数,用适当的数去乘方程的两边
消元:当未知数的系数相等时,将两个方程相减;当未知数的系数互为相反数时,将两个方程相加
求解:解消元后得到的一元一次方程
写:写出方程组的解
回代:把求得的未知数的值代入方程组中某个较简单的方程中
