人教版七年级数学下册课件:10.1 第2课时 抽样调查(21张)
文档属性
| 名称 | 人教版七年级数学下册课件:10.1 第2课时 抽样调查(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览







文档简介
第十章 数据的收集、整理与描述
10.1 第2课时 抽样调查
情境导入
小明这样买鸡蛋对吗?
妈妈:“小明,帮妈妈去买些鸡蛋”;
“这次要仔细挑选,上次你买的鸡蛋有几个是坏的.”
(一段时间过去了……)
小明:“妈妈,这次我买的鸡蛋全是好的”
妈妈:“很好,这次是怎么的?”
小明:“我每个都打开看过了”.
妈妈:“啊?!!!”
获取新知
问 题
某校有2000名学生,要想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,怎样进行调查?
可以用全面调查的方法对全校学生逐个进行调查,然后整理收集到的数据,统计出全校学生对五类电视节目的喜爱情况.
这样的操作是否高效呢?
但是,由于学生比较多,全面调查花费的时间长,消耗的人力、物力大.因此,需要寻找一种不作全面调查就能了解全校学生喜爱各类电视节目的情况的方法,达到既省时省力又能解决问题的目的.这就是我们要讨论的抽样调查.
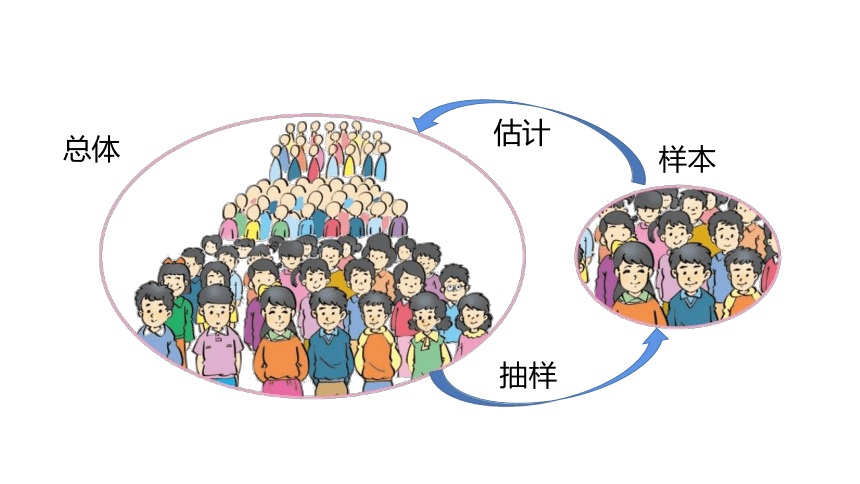
只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况,这种调查方法叫做抽样调查.
总体
样本
抽样
估计
抽样调查的几个组成部分:
要考察的全体对象称为总体.
组成总体的每一个考察对象称为个体.
被抽取的那些个体组成一个样本.
样本中个体的数目称为样本容量.
为了使抽取的样本具有代表性,要注意三点:
①样本容量适当;
②样本具有广泛性:当总体是由有明显差异的几个
部分组成时,每个部分都应被抽取到且比例适中;
③样本具有随机性,即保证每个个体被抽到的机会相等.
例如,上学时在学校门口随意调查100名学生;在全校学生的注册学号中,随意抽取100个学号,调查这些学号对应的学生;等等.
上面抽取样本的过程中,总体中的每一个个体都有相等的机会被抽到,像这样的抽样方法是一种简单随机抽样.(以后还会有分层抽样)
想一想:在这个问题中总体、个体、样本和样本容量分别是指什么?
总体为学校的全体学生的爱好情况;
个体为每个学生的爱好情况;
样本为所随机抽取100名学生的爱好情况.
样本容量为100
注意:总体,个体和样本都是指调查的数据,只是范围不同而已;而样本容量则为数字,不带单位
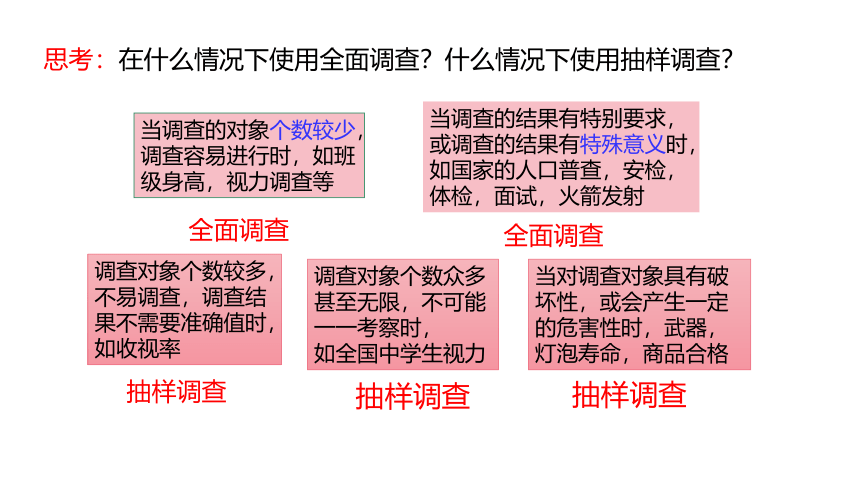
思考:在什么情况下使用全面调查?什么情况下使用抽样调查?
当调查的对象个数较少,调查容易进行时,如班级身高,视力调查等
全面调查
当调查的结果有特别要求,或调查的结果有特殊意义时,如国家的人口普查,安检,体检,面试,火箭发射
全面调查
调查对象个数较多,不易调查,调查结果不需要准确值时,如收视率
抽样调查
调查对象个数众多甚至无限,不可能一一考察时,
如全国中学生视力
抽样调查
当对调查对象具有破坏性,或会产生一定的危害性时,武器,灯泡寿命,商品合格
抽样调查
抽样调查
优 点
缺 点
全面调查
全面调查与抽样调查的比较
调查的结果准确,有利于全面了解数据.
工作量大,难度大,有时具有破坏性
工作量较小,省时省力,便于进行.
结果的准确性受样本影响,不能全面准确的了解数据.
例题讲解
例1 下列调查中,哪些适宜抽样调查,哪些适宜全面调查?
(1)调查我市中学生每天做作业的时间;
(2)调查某班学生对“中国梦”的知晓率;
(3)调查一架“歼20”隐形战机各零部件的质量;
(4)调查伦敦奥运会100 m跨栏决赛参赛运动员兴奋剂的使用情况.
解:(1)适宜抽样调查.(2)(3)(4)适宜全面调查.
例2 某市有3万名学生参加2019年的中考,想要了解这3万名考生的中考成绩,从中抽取了500名考生的中考成绩进行统计分析,以下说法正确的是( )
A.这500名考生是总体的一个样本
B.每个考生的中考成绩是个体
C.3万名考生是总体
D.500名考生是样本容量
B
例3 判断下列调查中样本的选取是否合适,并说明理由.
(1)在网上调查“你对老师讲课时‘拖堂现象’的态度”;
(2)在某一个敬老院里调查我国老年人的寿命情况;
(3)在校园里调查我国青年人上网的时间;
(4)为了了解我校七年级同学看电视的时间,随机选取了100名同学进行调查.
解:(1)不合适,因为网上调查只是一部分,不具有广泛性和代表性.
(2)不合适,因为敬老院里的老年人的寿命情况只是所有老年人的寿命情况中的一部分,还有非敬老院中的老年人的寿命情况也应该调查.
(3)不合适,因为校园学生只是青年人的一部分,还有非校园学生的青年人,校园学生上网的时间不代表所有青年人上网的时间.
(4)合适,因为抽样是随机的,样本具有代表性.
随堂演练
1.下列调查中,最适合采用抽样调查的是( ) A.对某校九年级(2)班学生体能测试达标情况的调查 B.对“神舟十一号”运载火箭发射前零部件质量状况的调查 C.对社区5名百岁以上老人的睡眠时间的调查 D.对市场上一批LED节能灯使用寿命的调查
D
2. 下面调查方式中,合适的是( )
A.调查你所在班级同学的身高,采用抽样调查方式
B.调查湘江的水质情况,采用抽样调查的方式
C.调查CCTV?5《NBA总决赛》栏目在我市的收视率,采用普查的方式
D.要了解全市初中学生的业余爱好,采用普查的方式
B
3.下列调查中,样本具有代表性的是( )
A.了解全校同学对课程的喜欢情况,对某班男同学进行调查
B.了解某小区居民的防火意识,对你们班同学进行调查
C.了解商场的平均日营业额,选在周末进行调查
D.了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查
D
4.在一次考试中,考生有2万名.为省时省力的了解这些考生的
数学平均成绩,抽取了500名考生的数学成绩进行调查.
(1)总体是________________;
(2)个体是________________;
(3)样本是________________;
(4)样本容量是__ .
2万名考生的数学成绩
其中每名考生的数学成绩
所抽取的500名考生的数学成绩
500
5. 近期,某市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书交流活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下不完整的统计图表,请根据图表中提供的信息,解答下面的问题: (1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度? (2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
{5940675A-B579-460E-94D1-54222C63F5DA}活动形式
征文
讲故事
演讲
网上竞答
其他
人数
60
30
39
A
B
解:(1)由题意得39÷13%=300(名), 扇形统计图中“讲故事”部分的圆心角是30÷300×360°=36°, 所以在这次抽样调查中,一共调查了300名学生,扇形统计图中“讲故事”部分的圆心角是36°. (2)由题意得3800×20%=760(名), 所以估计最喜爱征文活动的学生人数为760名.
课堂小结
抽样调查
样本的选择标准
总体、个体、样本、样本容量
抽样调查
简单随机抽样
收集数据的步骤
10.1 第2课时 抽样调查
情境导入
小明这样买鸡蛋对吗?
妈妈:“小明,帮妈妈去买些鸡蛋”;
“这次要仔细挑选,上次你买的鸡蛋有几个是坏的.”
(一段时间过去了……)
小明:“妈妈,这次我买的鸡蛋全是好的”
妈妈:“很好,这次是怎么的?”
小明:“我每个都打开看过了”.
妈妈:“啊?!!!”
获取新知
问 题
某校有2000名学生,要想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,怎样进行调查?
可以用全面调查的方法对全校学生逐个进行调查,然后整理收集到的数据,统计出全校学生对五类电视节目的喜爱情况.
这样的操作是否高效呢?
但是,由于学生比较多,全面调查花费的时间长,消耗的人力、物力大.因此,需要寻找一种不作全面调查就能了解全校学生喜爱各类电视节目的情况的方法,达到既省时省力又能解决问题的目的.这就是我们要讨论的抽样调查.
只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况,这种调查方法叫做抽样调查.
总体
样本
抽样
估计
抽样调查的几个组成部分:
要考察的全体对象称为总体.
组成总体的每一个考察对象称为个体.
被抽取的那些个体组成一个样本.
样本中个体的数目称为样本容量.
为了使抽取的样本具有代表性,要注意三点:
①样本容量适当;
②样本具有广泛性:当总体是由有明显差异的几个
部分组成时,每个部分都应被抽取到且比例适中;
③样本具有随机性,即保证每个个体被抽到的机会相等.
例如,上学时在学校门口随意调查100名学生;在全校学生的注册学号中,随意抽取100个学号,调查这些学号对应的学生;等等.
上面抽取样本的过程中,总体中的每一个个体都有相等的机会被抽到,像这样的抽样方法是一种简单随机抽样.(以后还会有分层抽样)
想一想:在这个问题中总体、个体、样本和样本容量分别是指什么?
总体为学校的全体学生的爱好情况;
个体为每个学生的爱好情况;
样本为所随机抽取100名学生的爱好情况.
样本容量为100
注意:总体,个体和样本都是指调查的数据,只是范围不同而已;而样本容量则为数字,不带单位
思考:在什么情况下使用全面调查?什么情况下使用抽样调查?
当调查的对象个数较少,调查容易进行时,如班级身高,视力调查等
全面调查
当调查的结果有特别要求,或调查的结果有特殊意义时,如国家的人口普查,安检,体检,面试,火箭发射
全面调查
调查对象个数较多,不易调查,调查结果不需要准确值时,如收视率
抽样调查
调查对象个数众多甚至无限,不可能一一考察时,
如全国中学生视力
抽样调查
当对调查对象具有破坏性,或会产生一定的危害性时,武器,灯泡寿命,商品合格
抽样调查
抽样调查
优 点
缺 点
全面调查
全面调查与抽样调查的比较
调查的结果准确,有利于全面了解数据.
工作量大,难度大,有时具有破坏性
工作量较小,省时省力,便于进行.
结果的准确性受样本影响,不能全面准确的了解数据.
例题讲解
例1 下列调查中,哪些适宜抽样调查,哪些适宜全面调查?
(1)调查我市中学生每天做作业的时间;
(2)调查某班学生对“中国梦”的知晓率;
(3)调查一架“歼20”隐形战机各零部件的质量;
(4)调查伦敦奥运会100 m跨栏决赛参赛运动员兴奋剂的使用情况.
解:(1)适宜抽样调查.(2)(3)(4)适宜全面调查.
例2 某市有3万名学生参加2019年的中考,想要了解这3万名考生的中考成绩,从中抽取了500名考生的中考成绩进行统计分析,以下说法正确的是( )
A.这500名考生是总体的一个样本
B.每个考生的中考成绩是个体
C.3万名考生是总体
D.500名考生是样本容量
B
例3 判断下列调查中样本的选取是否合适,并说明理由.
(1)在网上调查“你对老师讲课时‘拖堂现象’的态度”;
(2)在某一个敬老院里调查我国老年人的寿命情况;
(3)在校园里调查我国青年人上网的时间;
(4)为了了解我校七年级同学看电视的时间,随机选取了100名同学进行调查.
解:(1)不合适,因为网上调查只是一部分,不具有广泛性和代表性.
(2)不合适,因为敬老院里的老年人的寿命情况只是所有老年人的寿命情况中的一部分,还有非敬老院中的老年人的寿命情况也应该调查.
(3)不合适,因为校园学生只是青年人的一部分,还有非校园学生的青年人,校园学生上网的时间不代表所有青年人上网的时间.
(4)合适,因为抽样是随机的,样本具有代表性.
随堂演练
1.下列调查中,最适合采用抽样调查的是( ) A.对某校九年级(2)班学生体能测试达标情况的调查 B.对“神舟十一号”运载火箭发射前零部件质量状况的调查 C.对社区5名百岁以上老人的睡眠时间的调查 D.对市场上一批LED节能灯使用寿命的调查
D
2. 下面调查方式中,合适的是( )
A.调查你所在班级同学的身高,采用抽样调查方式
B.调查湘江的水质情况,采用抽样调查的方式
C.调查CCTV?5《NBA总决赛》栏目在我市的收视率,采用普查的方式
D.要了解全市初中学生的业余爱好,采用普查的方式
B
3.下列调查中,样本具有代表性的是( )
A.了解全校同学对课程的喜欢情况,对某班男同学进行调查
B.了解某小区居民的防火意识,对你们班同学进行调查
C.了解商场的平均日营业额,选在周末进行调查
D.了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查
D
4.在一次考试中,考生有2万名.为省时省力的了解这些考生的
数学平均成绩,抽取了500名考生的数学成绩进行调查.
(1)总体是________________;
(2)个体是________________;
(3)样本是________________;
(4)样本容量是__ .
2万名考生的数学成绩
其中每名考生的数学成绩
所抽取的500名考生的数学成绩
500
5. 近期,某市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书交流活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下不完整的统计图表,请根据图表中提供的信息,解答下面的问题: (1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度? (2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
{5940675A-B579-460E-94D1-54222C63F5DA}活动形式
征文
讲故事
演讲
网上竞答
其他
人数
60
30
39
A
B
解:(1)由题意得39÷13%=300(名), 扇形统计图中“讲故事”部分的圆心角是30÷300×360°=36°, 所以在这次抽样调查中,一共调查了300名学生,扇形统计图中“讲故事”部分的圆心角是36°. (2)由题意得3800×20%=760(名), 所以估计最喜爱征文活动的学生人数为760名.
课堂小结
抽样调查
样本的选择标准
总体、个体、样本、样本容量
抽样调查
简单随机抽样
收集数据的步骤
