人教版数学八年级上册 12.3.1角的平分线的性质 课件(22张)
文档属性
| 名称 | 人教版数学八年级上册 12.3.1角的平分线的性质 课件(22张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 12:56:50 | ||
图片预览



文档简介
12.3.1角的平分线的性质
学习目标
1.会用尺规作一个角的平分线,知道作法的合理性
2.探索并证明角的平分线的性质.
3.能用角的平分线的性质解决简单问题.
学习重点:
探索并证明角的平分线的性质.
问题1:在纸上画一个角,你能得到这个角的平分线?
导入新知
用量角器度量,也可用折纸的方法.
问题2:如果把前面的纸片换成木板、钢板等,还能用对折的方法得到木板、钢板的角平分线吗?
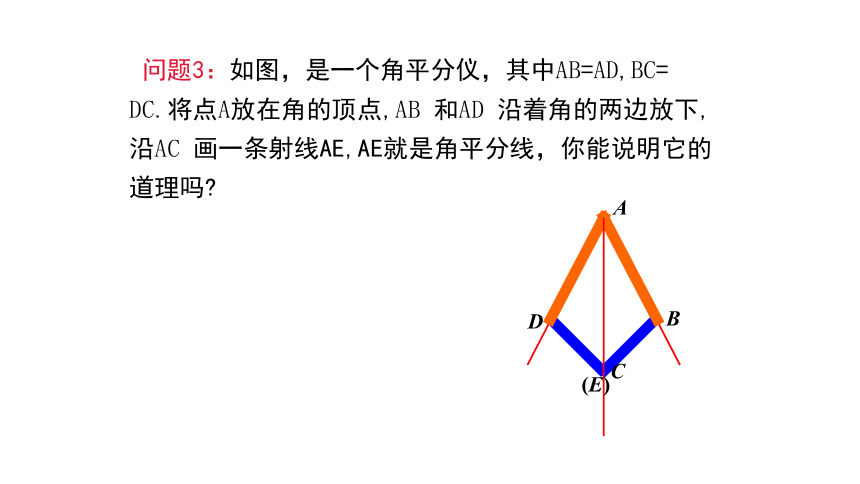
问题3:如图,是一个角平分仪,其中AB=AD,BC=
DC.将点A放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
B
C
(E)
D
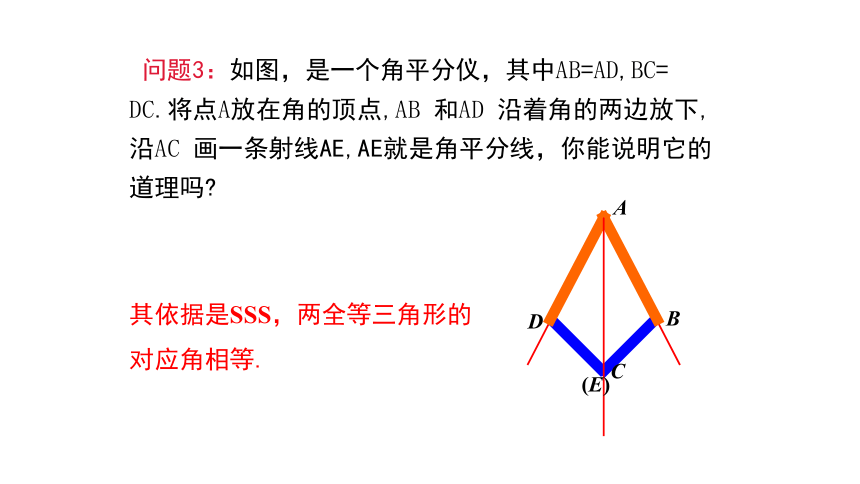
问题3:如图,是一个角平分仪,其中AB=AD,BC=
DC.将点A放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
B
C
(E)
D
其依据是SSS,两全等三角形的
对应角相等.
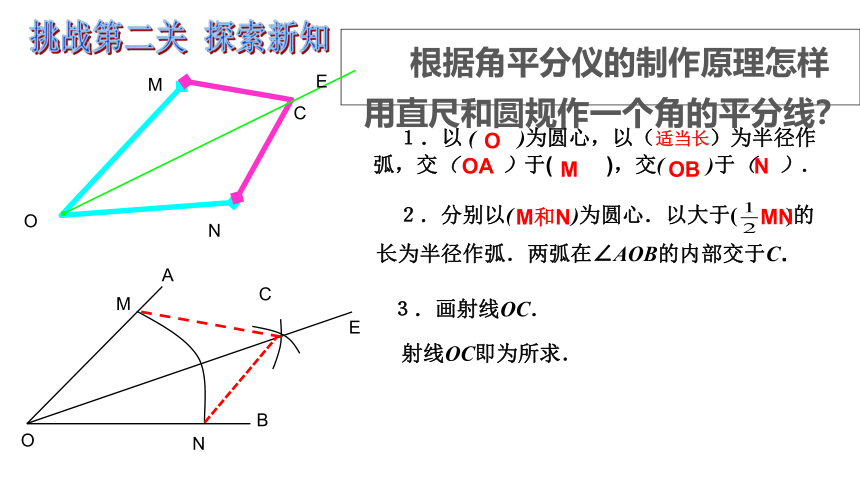
根据角平分仪的制作原理怎样用直尺和圆规作一个角的平分线?
O
A
B
C
E
N
O
M
C
E
N
M
1.以 ( )为圆心,以( )为半径作弧,交( )于( ),交( )于( ).
2.分别以( )为圆心.以大于( )的长为半径作弧.两弧在∠AOB的内部交于C.
3.画射线OC.
射线OC即为所求.
O
适当长
OA
M
OB
N
M和N
MN
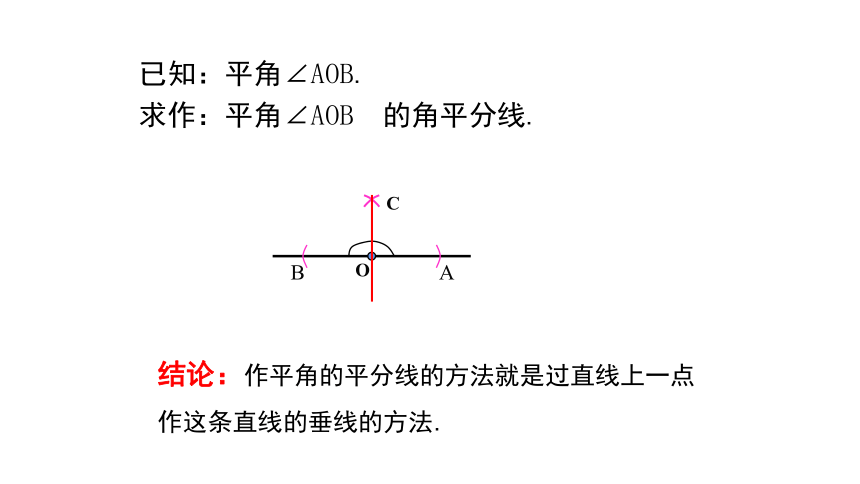
已知:平角∠AOB.
求作:平角∠AOB 的角平分线.
结论:作平角的平分线的方法就是过直线上一点作这条直线的垂线的方法.
A
B
O
C
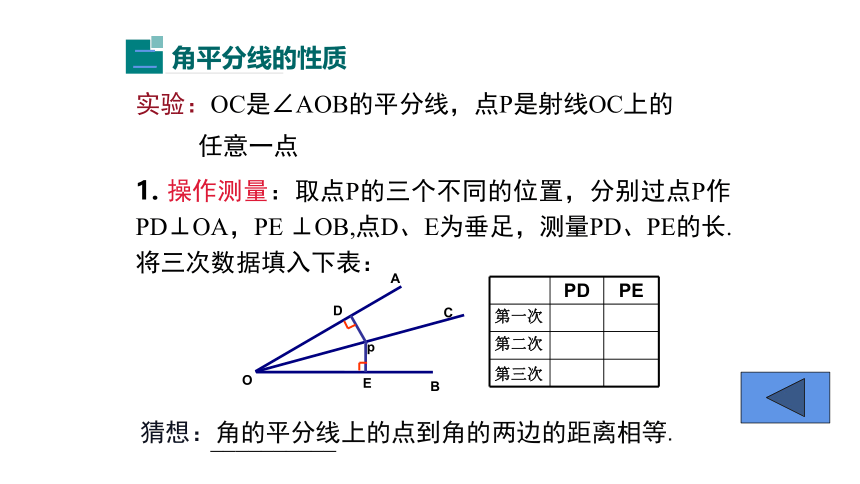
1. 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
2. 观察测量结果,猜想线段PD与PE的大小关系,写出结:__________
PD
PE
第一次
第二次
第三次
C
O
B
A
PD=PE
p
D
E
实验:OC是∠AOB的平分线,点P是射线OC上的
任意一点
猜想:角的平分线上的点到角的两边的距离相等.
角平分线的性质
二
验证猜想
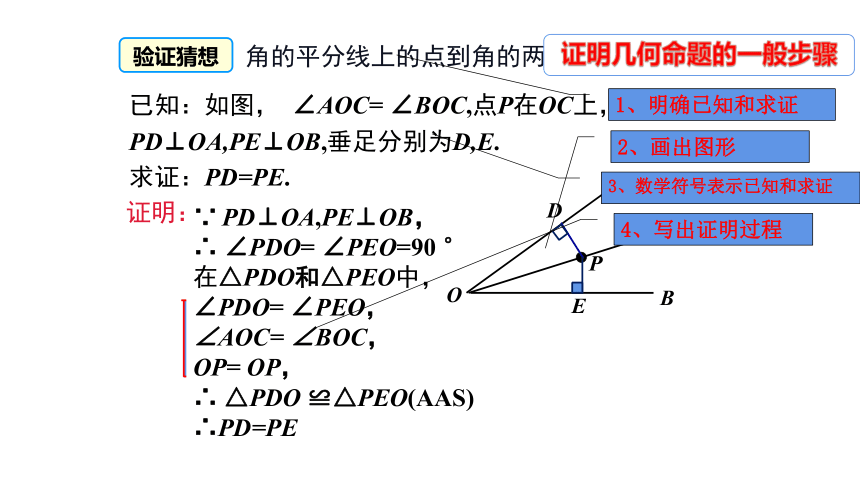
已知:如图, ∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
P
A
O
B
C
D
E
证明:
角的平分线上的点到角的两边的距离相等
3、数学符号表示已知和求证
2、画出图形
1、明确已知和求证
4、写出证明过程
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO= ∠PEO=90 °
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
∴ △PDO ≌△PEO(AAS)
∴PD=PE
性质:角的平分线上的点到角的两边的距离相等.
用符号语言表示为:
∵OP 是∠AOB的平分线,
∴PD = PE
推理的理由有三个,必须写完全,不能少了任何一个.
知识要点
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
判一判:(1)∵ 如下左图,AD平分∠BAC(已知),
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
(2)∵ 如上右图, DC⊥AC,DB⊥AB (已知).
∴ = ,
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
例1:已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB, DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
证明: ∵AD是∠BAC的角平分线, DE⊥AB, DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
DE=DF,
BD=CD,
∴ Rt△BDE ≌ Rt△CDF(HL).
∴ EB=FC.
典例精析
例2:如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D、E,PD=4cm,则PE=______cm.
B
A
C
P
M
D
E
4
温馨提示:存在两条垂线段———直接应用
典例精析
A
B
C
P
变式:如 图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4, AB=14.
(1)则点P到AB的距离为_______.
D
4
温馨提示:存在一条垂线段———构造应用
A
B
C
P
变式:如图,在Rt △ABC中,AC=BC,∠C=900,AP平分∠BAC交BC于点P,若PC=4,AB=14.
(2)求△APB的面积.
D
(3)求?PDB的周长.
·AB·PD=28.
由垂直平分线的性质,可知,PD=PC=4,
●请你把这节课你学到的知
识或体验的感受先告诉你的
同桌,然后再告诉老师?
归纳小结
当堂检测
当堂检测
当堂检测
当堂检测
3.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.点M
B.点N
C.点P
D.点Q
当堂检测
当堂检测
A
C
D
B
E
4.如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,BC=7㎝,DE=3㎝,求BD= ㎝.
当堂检测
当堂检测
A
C
D
B
E
5.如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,BC=7㎝,DE=3㎝,求BD= ㎝.
当堂检测
当堂检测
课后作业
作业
内容
必做作业
课本51页 第2、3题
选做作业
智慧学习42页 第2、3题
学习目标
1.会用尺规作一个角的平分线,知道作法的合理性
2.探索并证明角的平分线的性质.
3.能用角的平分线的性质解决简单问题.
学习重点:
探索并证明角的平分线的性质.
问题1:在纸上画一个角,你能得到这个角的平分线?
导入新知
用量角器度量,也可用折纸的方法.
问题2:如果把前面的纸片换成木板、钢板等,还能用对折的方法得到木板、钢板的角平分线吗?
问题3:如图,是一个角平分仪,其中AB=AD,BC=
DC.将点A放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
B
C
(E)
D
问题3:如图,是一个角平分仪,其中AB=AD,BC=
DC.将点A放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
B
C
(E)
D
其依据是SSS,两全等三角形的
对应角相等.
根据角平分仪的制作原理怎样用直尺和圆规作一个角的平分线?
O
A
B
C
E
N
O
M
C
E
N
M
1.以 ( )为圆心,以( )为半径作弧,交( )于( ),交( )于( ).
2.分别以( )为圆心.以大于( )的长为半径作弧.两弧在∠AOB的内部交于C.
3.画射线OC.
射线OC即为所求.
O
适当长
OA
M
OB
N
M和N
MN
已知:平角∠AOB.
求作:平角∠AOB 的角平分线.
结论:作平角的平分线的方法就是过直线上一点作这条直线的垂线的方法.
A
B
O
C
1. 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
2. 观察测量结果,猜想线段PD与PE的大小关系,写出结:__________
PD
PE
第一次
第二次
第三次
C
O
B
A
PD=PE
p
D
E
实验:OC是∠AOB的平分线,点P是射线OC上的
任意一点
猜想:角的平分线上的点到角的两边的距离相等.
角平分线的性质
二
验证猜想
已知:如图, ∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
P
A
O
B
C
D
E
证明:
角的平分线上的点到角的两边的距离相等
3、数学符号表示已知和求证
2、画出图形
1、明确已知和求证
4、写出证明过程
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO= ∠PEO=90 °
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
∴ △PDO ≌△PEO(AAS)
∴PD=PE
性质:角的平分线上的点到角的两边的距离相等.
用符号语言表示为:
∵OP 是∠AOB的平分线,
∴PD = PE
推理的理由有三个,必须写完全,不能少了任何一个.
知识要点
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
判一判:(1)∵ 如下左图,AD平分∠BAC(已知),
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
(2)∵ 如上右图, DC⊥AC,DB⊥AB (已知).
∴ = ,
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
例1:已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB, DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
证明: ∵AD是∠BAC的角平分线, DE⊥AB, DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
DE=DF,
BD=CD,
∴ Rt△BDE ≌ Rt△CDF(HL).
∴ EB=FC.
典例精析
例2:如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D、E,PD=4cm,则PE=______cm.
B
A
C
P
M
D
E
4
温馨提示:存在两条垂线段———直接应用
典例精析
A
B
C
P
变式:如 图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4, AB=14.
(1)则点P到AB的距离为_______.
D
4
温馨提示:存在一条垂线段———构造应用
A
B
C
P
变式:如图,在Rt △ABC中,AC=BC,∠C=900,AP平分∠BAC交BC于点P,若PC=4,AB=14.
(2)求△APB的面积.
D
(3)求?PDB的周长.
·AB·PD=28.
由垂直平分线的性质,可知,PD=PC=4,
●请你把这节课你学到的知
识或体验的感受先告诉你的
同桌,然后再告诉老师?
归纳小结
当堂检测
当堂检测
当堂检测
当堂检测
3.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.点M
B.点N
C.点P
D.点Q
当堂检测
当堂检测
A
C
D
B
E
4.如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,BC=7㎝,DE=3㎝,求BD= ㎝.
当堂检测
当堂检测
A
C
D
B
E
5.如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,BC=7㎝,DE=3㎝,求BD= ㎝.
当堂检测
当堂检测
课后作业
作业
内容
必做作业
课本51页 第2、3题
选做作业
智慧学习42页 第2、3题
