人教版数学九年 级下册27.1章前引言及相似图形课件(42张)
文档属性
| 名称 | 人教版数学九年 级下册27.1章前引言及相似图形课件(42张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览






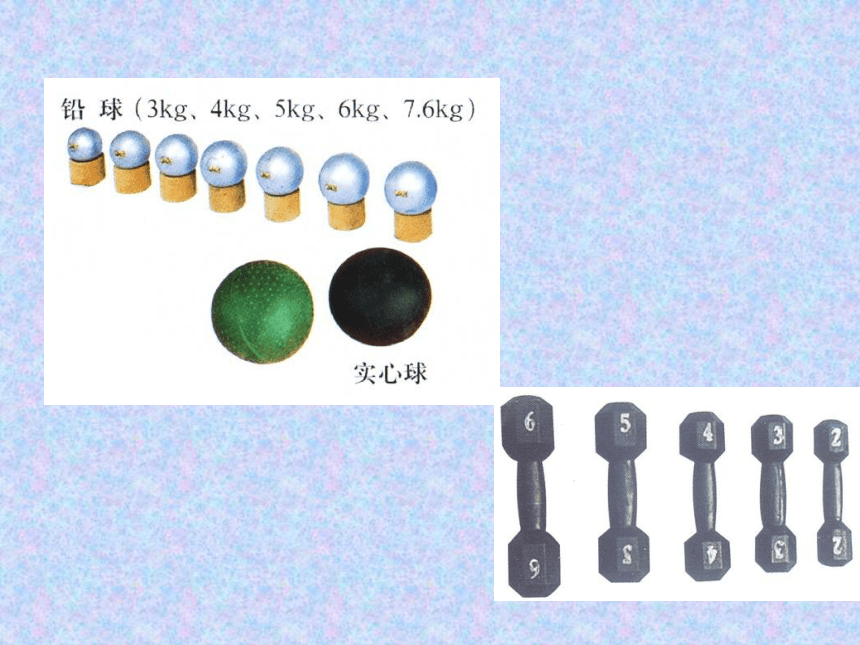



文档简介
相似图形
相似图形
相似图形
27.1 图形的相似
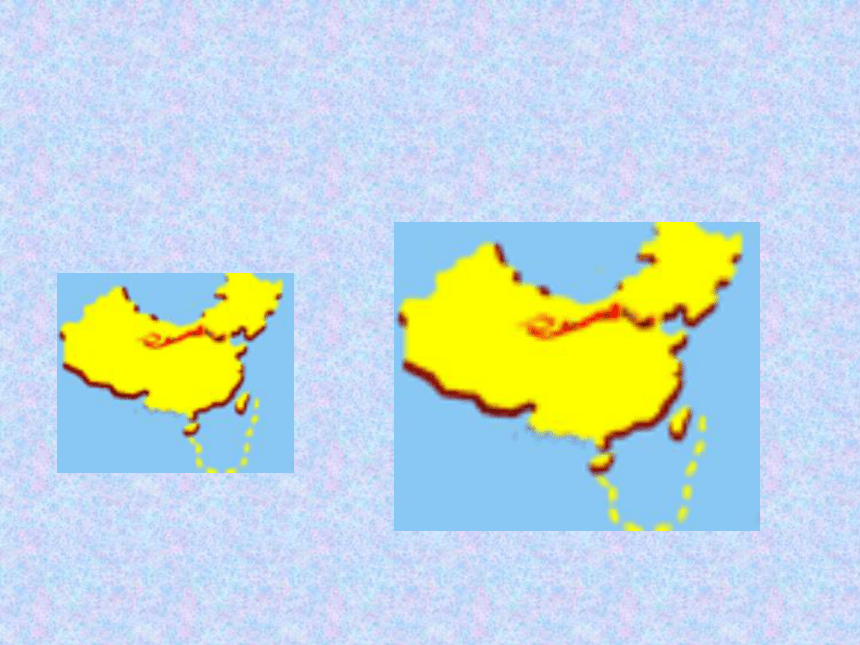
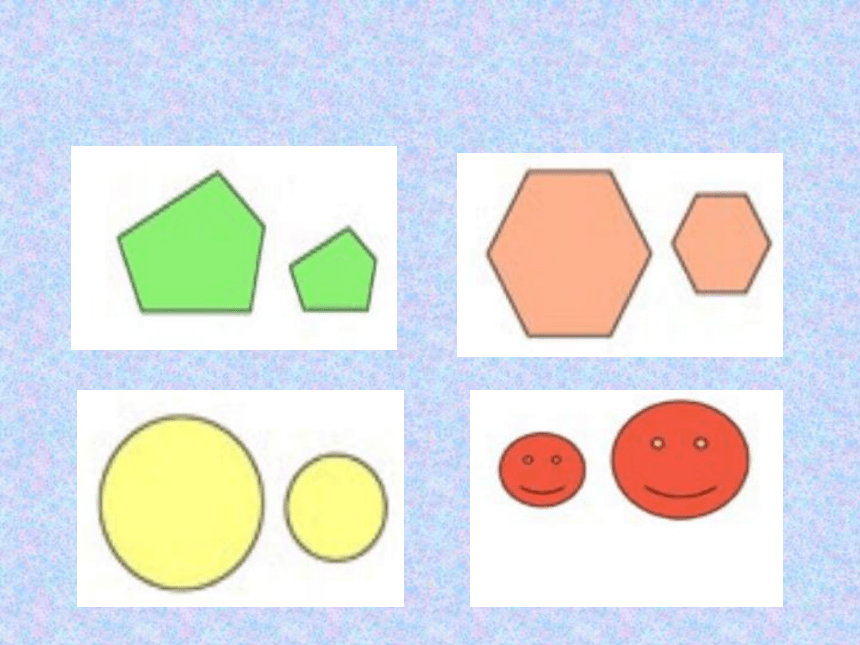
观察左右两张图片有什么关系?
请观察下面几组图片
你从上述几组图片发现了什么?
它们的大小不一定相等,
形状相同.
相似图形的概念:
在数学上,我们把具有相同形状的图形称为相似图形。
注意:相似图形的大小不一定相同。
全等的两个三角形相似吗?
思考
A
B
C
B
C
A
形状、大小都相同的图形称为全等形。
全等图形:
全等图形与相似图形的关系:
全等形是相似形的特殊情况。
(5)
(6)
(1)
(2)
(3)
(7)
(4)
(12)
(14)
(8)
(9)
(10)
(13)
(11)
观察下图,哪些图形是相似图形?
解: ①相似 ②不相似 ③不相似
④相似 ⑤不相似 ⑥不相似
请把下列各组图形是否相似的结论写在下面的括号里.
试一试
探究相似多边形的特征
相似多边形是较简单的相似图形,而相似三角形是最简单的相似多边形,下面我们以相似三角形为例探讨相似多边形的特征
两个相似三角形的对应角有什么关系?
两个相似三角形的对应边有什么关系?
思考
表示为:
△ABC∽△ A'B'C'
C
A
B
A/
B/
C/
在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上。
A
A/
B/
B
C
C/
A
A'
B/
B
C
C/
注意
读作:
△ABC相似于△ A'B'C'
△ABC与△ A'B'C'相似
相似三角形特征(在相似多边形中,最简单的就是相似三角形):对应角相等,对应边的比相等。
用符号语言表示:
∵
∠A= ∠A' 、∠B= ∠B' 、∠C=C'
∴ △ABC∽△A'B'C'
(相似三角形的特征可以作为三角形相似的一种判定方法)
C
B
A
D
F
E
如图,ΔABC∽ ΔDFE
则它们的对应角分别是∠A与∠_____,
∠B与∠_____,
∠C与∠_____;
对应边成比例的是
D
F
E
E
F
D
C
B
A
7
6
2
12
14
4
和
相似
∠A =∠_____,
∠B =∠_____,
∠C =∠_____;
E
D
F
E
F
D
C
B
A
和
相似
K表示这两个相似三角形
的相似比
? 相似比就是它们的对应边的比
? 它有顺序关系
∽
它的相似比为K
∽
它的相似比为
C
A
B
A'
B'
C'
6cm
3cm
△ABC与△A'B'C'的
相似比k1
△A'B'C'与△ABC的相似比k2
=?
=?
△ABC∽△A'B'C'
例如:
三角形的前后次序不同,所得相似比不同。
A B D F
八年级 数学
A`
B`
C`
把三角形ABC放大到原来的两倍(要求:放大后的顶点在格点上)。
画一画
八年级 数学
C`
B`
A`
D`
把四边形ABCD放大1倍(要求:放大后的顶点在格点上)。
练一练
如下图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形。
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
动动手
如图,
∽
,写出三对对应角
________=_________,
_________=________,
________=_________,
若ΔABC∽△AEF的相似比是3:2 ,EF=8cm,则BC= cm。
F
E
C
B
A
1
2
3
基础训练
1、口答:
(1)如图所示的两个三角形是否相似?
基础训练
口答:
(2)如图,正方形的边长a=10,菱形的
边长b=5,它们相似吗?请说明理由.
基础训练
2、填空:
(1)等腰三角形两腰的比是________;
(2)直角三 角形斜边上的中线和斜边的
比是_________.
1∶1
1∶2
3、判断下列两个三角形是否相似?简单说明理由,如果相似,写出对应边的比例
4、 在下面的两组图形中,各有两个相似三角形,试确定x , y , m , n 的值。
x
20
33
48
22
30
45°
85°
m°
n°
50°
45°
3a
2a
y
10
4、 在如图所示的相似四边形中, 求未知边x、
y的长度和角度a的大小.
解:由于两个四边形相似,它们的对应边成比例,对应角相等,所以
解得 x=31.5,y=27
a =360°-(77°+83°+117°)=83°
相似图形 ——相同形状的图形
利用相似放大或缩小图形
相似多边形
特征
识别
对应角相等
对应边成比例
相似多边形的特征和识别:
判断两个图形是否相似
三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形。
△ABC与△DEF相似,就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
相似三角形的各对应角相等,各对应边对应成比例。
相似比就是它们的对应边的比
课堂小结
相似图形
相似图形
27.1 图形的相似
观察左右两张图片有什么关系?
请观察下面几组图片
你从上述几组图片发现了什么?
它们的大小不一定相等,
形状相同.
相似图形的概念:
在数学上,我们把具有相同形状的图形称为相似图形。
注意:相似图形的大小不一定相同。
全等的两个三角形相似吗?
思考
A
B
C
B
C
A
形状、大小都相同的图形称为全等形。
全等图形:
全等图形与相似图形的关系:
全等形是相似形的特殊情况。
(5)
(6)
(1)
(2)
(3)
(7)
(4)
(12)
(14)
(8)
(9)
(10)
(13)
(11)
观察下图,哪些图形是相似图形?
解: ①相似 ②不相似 ③不相似
④相似 ⑤不相似 ⑥不相似
请把下列各组图形是否相似的结论写在下面的括号里.
试一试
探究相似多边形的特征
相似多边形是较简单的相似图形,而相似三角形是最简单的相似多边形,下面我们以相似三角形为例探讨相似多边形的特征
两个相似三角形的对应角有什么关系?
两个相似三角形的对应边有什么关系?
思考
表示为:
△ABC∽△ A'B'C'
C
A
B
A/
B/
C/
在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上。
A
A/
B/
B
C
C/
A
A'
B/
B
C
C/
注意
读作:
△ABC相似于△ A'B'C'
△ABC与△ A'B'C'相似
相似三角形特征(在相似多边形中,最简单的就是相似三角形):对应角相等,对应边的比相等。
用符号语言表示:
∵
∠A= ∠A' 、∠B= ∠B' 、∠C=C'
∴ △ABC∽△A'B'C'
(相似三角形的特征可以作为三角形相似的一种判定方法)
C
B
A
D
F
E
如图,ΔABC∽ ΔDFE
则它们的对应角分别是∠A与∠_____,
∠B与∠_____,
∠C与∠_____;
对应边成比例的是
D
F
E
E
F
D
C
B
A
7
6
2
12
14
4
和
相似
∠A =∠_____,
∠B =∠_____,
∠C =∠_____;
E
D
F
E
F
D
C
B
A
和
相似
K表示这两个相似三角形
的相似比
? 相似比就是它们的对应边的比
? 它有顺序关系
∽
它的相似比为K
∽
它的相似比为
C
A
B
A'
B'
C'
6cm
3cm
△ABC与△A'B'C'的
相似比k1
△A'B'C'与△ABC的相似比k2
=?
=?
△ABC∽△A'B'C'
例如:
三角形的前后次序不同,所得相似比不同。
A B D F
八年级 数学
A`
B`
C`
把三角形ABC放大到原来的两倍(要求:放大后的顶点在格点上)。
画一画
八年级 数学
C`
B`
A`
D`
把四边形ABCD放大1倍(要求:放大后的顶点在格点上)。
练一练
如下图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形。
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
动动手
如图,
∽
,写出三对对应角
________=_________,
_________=________,
________=_________,
若ΔABC∽△AEF的相似比是3:2 ,EF=8cm,则BC= cm。
F
E
C
B
A
1
2
3
基础训练
1、口答:
(1)如图所示的两个三角形是否相似?
基础训练
口答:
(2)如图,正方形的边长a=10,菱形的
边长b=5,它们相似吗?请说明理由.
基础训练
2、填空:
(1)等腰三角形两腰的比是________;
(2)直角三 角形斜边上的中线和斜边的
比是_________.
1∶1
1∶2
3、判断下列两个三角形是否相似?简单说明理由,如果相似,写出对应边的比例
4、 在下面的两组图形中,各有两个相似三角形,试确定x , y , m , n 的值。
x
20
33
48
22
30
45°
85°
m°
n°
50°
45°
3a
2a
y
10
4、 在如图所示的相似四边形中, 求未知边x、
y的长度和角度a的大小.
解:由于两个四边形相似,它们的对应边成比例,对应角相等,所以
解得 x=31.5,y=27
a =360°-(77°+83°+117°)=83°
相似图形 ——相同形状的图形
利用相似放大或缩小图形
相似多边形
特征
识别
对应角相等
对应边成比例
相似多边形的特征和识别:
判断两个图形是否相似
三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形。
△ABC与△DEF相似,就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
相似三角形的各对应角相等,各对应边对应成比例。
相似比就是它们的对应边的比
课堂小结
