人教版 八年级上册数学 12.2 三角形全等的判定 课时训练(word含答案)
文档属性
| 名称 | 人教版 八年级上册数学 12.2 三角形全等的判定 课时训练(word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 399.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 12:10:42 | ||
图片预览


文档简介
人教版 八年级数学 12.2 三角形全等的判定 课时训练
一、选择题
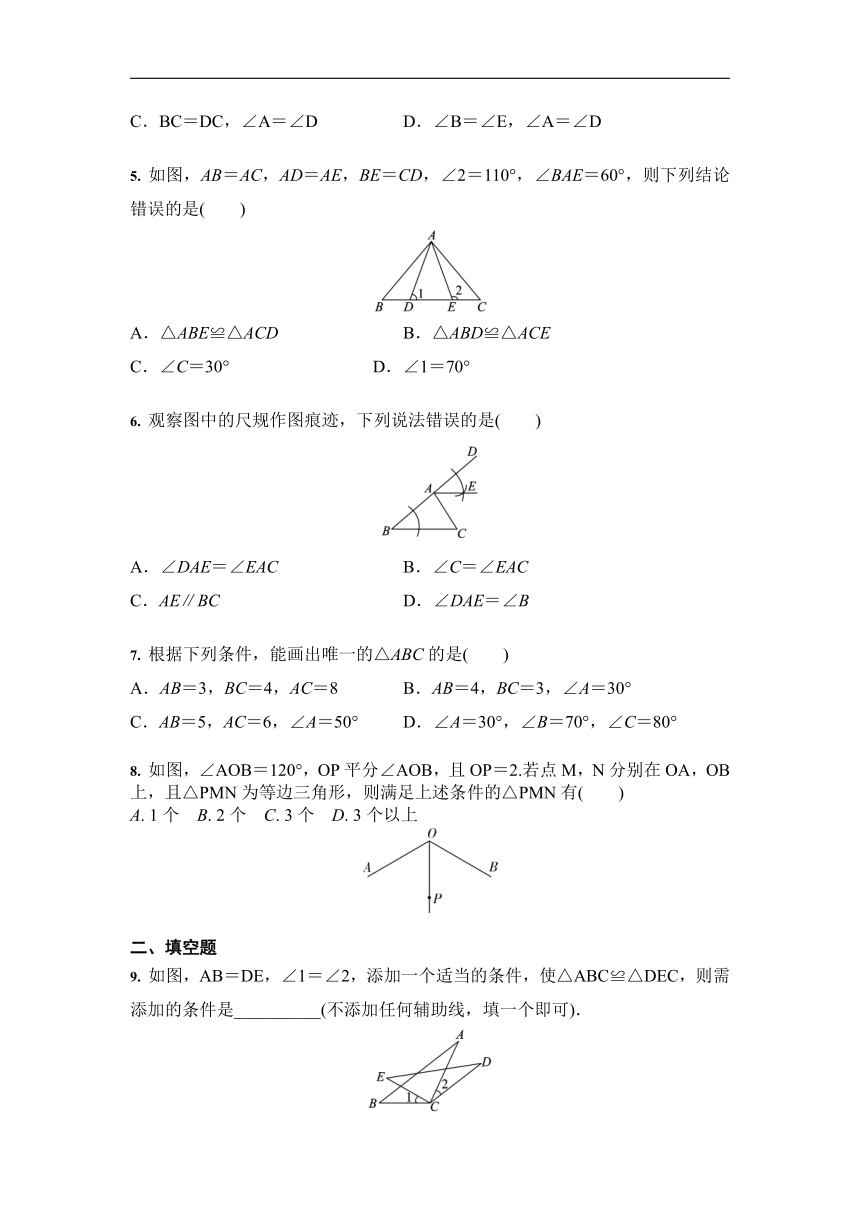
1. 在如图所示的三角形中,与图中的△ABC全等的是( )
2. 如图,在正方形ABCD中,连接BD,点O是BD的中点.若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A. 2对 B. 3对 C. 4对 D. 5对
3. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到
玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去 ( )
A. ① B. ②
C. ③ D. ①和②
4. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
5. 如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是( )
A.△ABE≌△ACD B.△ABD≌△ACE
C.∠C=30° D.∠1=70°
6. 观察图中的尺规作图痕迹,下列说法错误的是( )
A.∠DAE=∠EAC B.∠C=∠EAC
C.AE∥BC D.∠DAE=∠B
7. 根据下列条件,能画出唯一的△ABC的是( )
A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°
C.AB=5,AC=6,∠A=50° D.∠A=30°,∠B=70°,∠C=80°
8. 如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
A. 1个 B. 2个 C. 3个 D. 3个以上
二、填空题
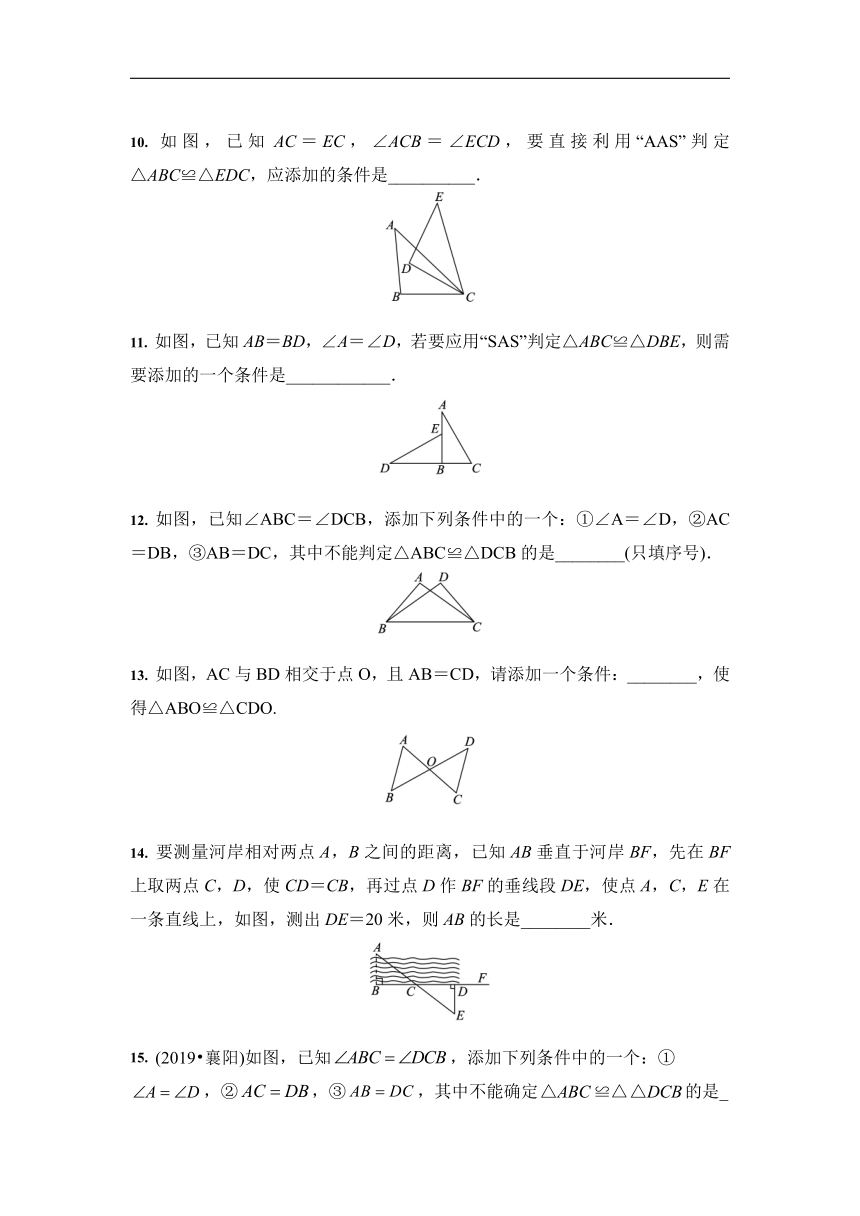
9. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
10. 如图,已知AC=EC,∠ACB=∠ECD,要直接利用“AAS”判定△ABC≌△EDC,应添加的条件是__________.
11. 如图,已知AB=BD,∠A=∠D,若要应用“SAS”判定△ABC≌△DBE,则需要添加的一个条件是____________.
12. 如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D,②AC=DB,③AB=DC,其中不能判定△ABC≌△DCB的是________(只填序号).
13. 如图,AC与BD相交于点O,且AB=CD,请添加一个条件:________,使得△ABO≌△CDO.
14. 要测量河岸相对两点A,B之间的距离,已知AB垂直于河岸BF,先在BF上取两点C,D,使CD=CB,再过点D作BF的垂线段DE,使点A,C,E在一条直线上,如图,测出DE=20米,则AB的长是________米.
15. (2019?襄阳)如图,已知,添加下列条件中的一个:①,②,③,其中不能确定≌△的是__________(只填序号).
16. 如图,在Rt△ABC中,∠C=90°,E为AB的中点,D为AC上一点,BF∥AC,交DE的延长线于点F,AC=6,BC=5,则四边形FBCD周长的最小值是 .
三、解答题
17. 如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD.求证:CF=DE.
18. 如图,在△ABC中,AB=AC,BE⊥AC于点E,CD⊥AB于点D,BE,CD相交于点F,连接AF.
求证:(1)△AEB≌△ADC;
(2)AF平分∠BAC.
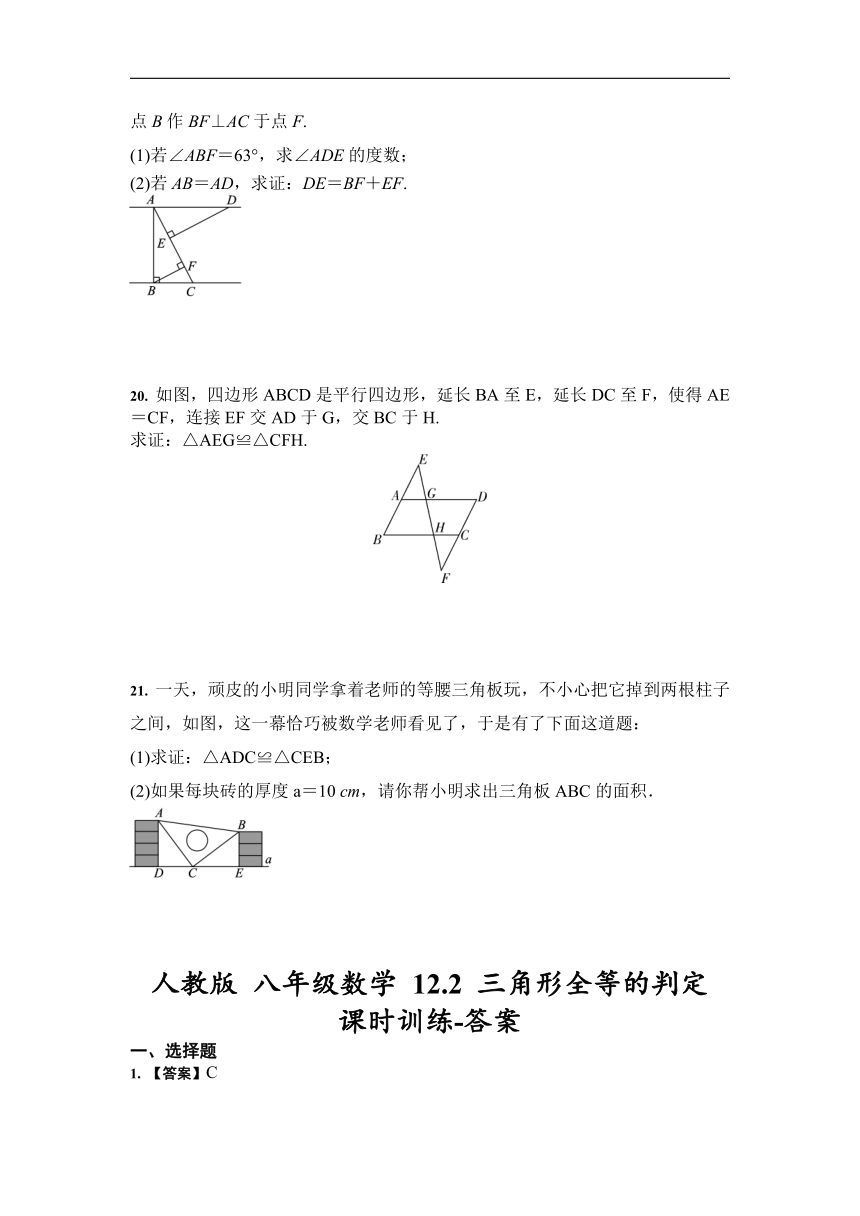
19. 如图,AD∥BC,AB⊥BC于点B,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.
(1)若∠ABF=63°,求∠ADE的度数;
(2)若AB=AD,求证:DE=BF+EF.
20. 如图,四边形ABCD是平行四边形,延长BA至E,延长DC至F,使得AE=CF,连接EF交AD于G,交BC于H.
求证:△AEG≌△CFH.
21. 一天,顽皮的小明同学拿着老师的等腰三角板玩,不小心把它掉到两根柱子之间,如图,这一幕恰巧被数学老师看见了,于是有了下面这道题:
(1)求证:△ADC≌△CEB;
(2)如果每块砖的厚度a=10 cm,请你帮小明求出三角板ABC的面积.
人教版 八年级数学 12.2 三角形全等的判定 课时训练-答案
一、选择题
1. 【答案】C
2. 【答案】C 【解析】由题意可知,△ABD≌△CBD,△MON≌△M′ON′,△DON≌△BON′,△DOM≌△BOM′共4对.
3. 【答案】 C
4. 【答案】C
5. 【答案】C [解析] ∵BE=CD,
∴BE-DE=CD-DE,即BD=CE.
在△ABD和△ACE中,
∴△ABD≌△ACE.
由题意易证:△ABE≌△ACD,故A,B正确.
由△ABE≌△ACD可得∠B=∠C.
∵∠2=∠BAE+∠B,
∴∠B=∠2-∠BAE=110°-60°=50°.
∴∠C=∠B=50°.
故C错误.
∵△ABE≌△ACD(已证),∴∠1=∠AED=180°-∠2=70°.
故D正确.故选C.
6. 【答案】A [解析] 根据图中尺规作图的痕迹,可得∠DAE=∠B,故D选项正确,∴AE∥BC,故C选项正确.∴∠EAC=∠C,故B选项正确.
∵∠DAE=∠B,∠EAC=∠C,而∠C与∠B的大小关系不确定,所以∠DAE与∠EAC的大小关系不确定.故选A.
7. 【答案】C [解析] 对于选项A来说,AB+BC8. 【答案】D 【解析】如解图,①当OM1=2时,点N1与点O重合,△PMN是等边三角形;②当ON2=2时,点M2与点O重合,△PMN是等边三角形;③当点M3,N3分别是OM1,ON2的中点时,△PMN是等边三角形;④当取∠M1PM4=∠OPN4时,易证△M1PM4≌△OPN4(SAS),∴PM4=PN4,又∵∠M4PN4=60°,∴△PMN是等边三角形,此时点M,N有无数个,综上所述,故选D.
二、填空题
9. 【答案】答案不唯一,如∠B=∠E
10. 【答案】∠B=∠D
11. 【答案】AC=DE
12. 【答案】② [解析] ∵已知∠ABC=∠DCB,且BC=CB,
∴若添加①∠A=∠D,则可由“AAS”判定△ABC≌△DCB;
若添加②AC=DB,则属于“SSA”,不能判定△ABC≌△DCB;
若添加③AB=DC,则可由“SAS”判定△ABC≌△DCB.
13. 【答案】∠A=∠C或∠B=∠D或AB∥CD(答案不唯一)
[解析] 由题意可知∠AOB=∠COD,AB=CD.
∵AB是∠AOB的对边,CD是∠COD的对边,∴只能添加角相等,故可添加∠A=∠C或∠B=∠D或AB∥CD.
14. 【答案】20
15. 【答案】②
【解析】∵已知,且,
∴若添加①,则可由AAS判定≌;
若添加②,则属于边边角的顺序,不能判定≌;
若添加③,则属于边角边的顺序,可以判定≌.
故答案为:②.
16. 【答案】16 [解析] ∵BF∥AC,
∴∠EBF=∠EAD.
在△BFE和△ADE中,
∴△BFE≌△ADE(ASA).∴BF=AD.
∴BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD.
∵当FD⊥AC时,FD最短,此时FD=BC=5,
∴四边形FBCD周长的最小值为5+11=16.
三、解答题
17. 【答案】
证明:∵AE=BF,∴AE+EF=BF+EF,
即AF=BE.
∵AC∥BD,∴∠CAF=∠DBE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS).
∴CF=DE.
18. 【答案】
证明:(1)∵BE⊥AC,CD⊥AB,
∴∠AEB=∠ADC=90°.
在△AEB与△ADC中,
∴△AEB≌△ADC(AAS).
(2)∵△AEB≌△ADC,∴AE=AD.
在Rt△AEF与Rt△ADF中,
∴Rt△AEF≌Rt△ADF(HL).
∴∠EAF=∠DAF.∴AF平分∠BAC.
19. 【答案】
解:(1)∵AD∥BC,AB⊥BC,
∴∠ABC=∠BAD=90°.
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠AED=90°.
∴∠ABF+∠BAF=∠BAF+∠DAE=90°.
∴∠DAE=∠ABF=63°.∴∠ADE=27°.
(2)证明:由(1)得∠DAE=∠ABF,∠AED=∠BFA=90°.
在△DAE和△ABF中,
∴△DAE≌△ABF(AAS).
∴AE=BF,DE=AF.
∴DE=AF=AE+EF=BF+EF.
20. 【答案】
证明:∵在?ABCD中,∠BAD=∠BCD,AB∥CD,
∴∠E=∠F,180°-∠BAD=180°-∠BCD,即∠EAG=∠FCH,(5分)
在△AEG和△CFH中,
,
∴△AEG≌△CFH(ASA).(7分)
21. 【答案】
解:(1)证明:由题意得AC=CB,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°.
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°.∴∠BCE=∠CAD.
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS).
(2)由(1)知△ADC≌△CEB,
∴AD=CE=4a=40 cm,CD=BE=3a=30 cm.
∴DE=70 cm.
∴S△ABC=×(30+40)×70-2××30×40=1250(cm2).
答:三角板ABC的面积为1250 cm2.
一、选择题
1. 在如图所示的三角形中,与图中的△ABC全等的是( )
2. 如图,在正方形ABCD中,连接BD,点O是BD的中点.若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A. 2对 B. 3对 C. 4对 D. 5对
3. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到
玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去 ( )
A. ① B. ②
C. ③ D. ①和②
4. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
5. 如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是( )
A.△ABE≌△ACD B.△ABD≌△ACE
C.∠C=30° D.∠1=70°
6. 观察图中的尺规作图痕迹,下列说法错误的是( )
A.∠DAE=∠EAC B.∠C=∠EAC
C.AE∥BC D.∠DAE=∠B
7. 根据下列条件,能画出唯一的△ABC的是( )
A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°
C.AB=5,AC=6,∠A=50° D.∠A=30°,∠B=70°,∠C=80°
8. 如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
A. 1个 B. 2个 C. 3个 D. 3个以上
二、填空题
9. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
10. 如图,已知AC=EC,∠ACB=∠ECD,要直接利用“AAS”判定△ABC≌△EDC,应添加的条件是__________.
11. 如图,已知AB=BD,∠A=∠D,若要应用“SAS”判定△ABC≌△DBE,则需要添加的一个条件是____________.
12. 如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D,②AC=DB,③AB=DC,其中不能判定△ABC≌△DCB的是________(只填序号).
13. 如图,AC与BD相交于点O,且AB=CD,请添加一个条件:________,使得△ABO≌△CDO.
14. 要测量河岸相对两点A,B之间的距离,已知AB垂直于河岸BF,先在BF上取两点C,D,使CD=CB,再过点D作BF的垂线段DE,使点A,C,E在一条直线上,如图,测出DE=20米,则AB的长是________米.
15. (2019?襄阳)如图,已知,添加下列条件中的一个:①,②,③,其中不能确定≌△的是__________(只填序号).
16. 如图,在Rt△ABC中,∠C=90°,E为AB的中点,D为AC上一点,BF∥AC,交DE的延长线于点F,AC=6,BC=5,则四边形FBCD周长的最小值是 .
三、解答题
17. 如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD.求证:CF=DE.
18. 如图,在△ABC中,AB=AC,BE⊥AC于点E,CD⊥AB于点D,BE,CD相交于点F,连接AF.
求证:(1)△AEB≌△ADC;
(2)AF平分∠BAC.
19. 如图,AD∥BC,AB⊥BC于点B,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.
(1)若∠ABF=63°,求∠ADE的度数;
(2)若AB=AD,求证:DE=BF+EF.
20. 如图,四边形ABCD是平行四边形,延长BA至E,延长DC至F,使得AE=CF,连接EF交AD于G,交BC于H.
求证:△AEG≌△CFH.
21. 一天,顽皮的小明同学拿着老师的等腰三角板玩,不小心把它掉到两根柱子之间,如图,这一幕恰巧被数学老师看见了,于是有了下面这道题:
(1)求证:△ADC≌△CEB;
(2)如果每块砖的厚度a=10 cm,请你帮小明求出三角板ABC的面积.
人教版 八年级数学 12.2 三角形全等的判定 课时训练-答案
一、选择题
1. 【答案】C
2. 【答案】C 【解析】由题意可知,△ABD≌△CBD,△MON≌△M′ON′,△DON≌△BON′,△DOM≌△BOM′共4对.
3. 【答案】 C
4. 【答案】C
5. 【答案】C [解析] ∵BE=CD,
∴BE-DE=CD-DE,即BD=CE.
在△ABD和△ACE中,
∴△ABD≌△ACE.
由题意易证:△ABE≌△ACD,故A,B正确.
由△ABE≌△ACD可得∠B=∠C.
∵∠2=∠BAE+∠B,
∴∠B=∠2-∠BAE=110°-60°=50°.
∴∠C=∠B=50°.
故C错误.
∵△ABE≌△ACD(已证),∴∠1=∠AED=180°-∠2=70°.
故D正确.故选C.
6. 【答案】A [解析] 根据图中尺规作图的痕迹,可得∠DAE=∠B,故D选项正确,∴AE∥BC,故C选项正确.∴∠EAC=∠C,故B选项正确.
∵∠DAE=∠B,∠EAC=∠C,而∠C与∠B的大小关系不确定,所以∠DAE与∠EAC的大小关系不确定.故选A.
7. 【答案】C [解析] 对于选项A来说,AB+BC
二、填空题
9. 【答案】答案不唯一,如∠B=∠E
10. 【答案】∠B=∠D
11. 【答案】AC=DE
12. 【答案】② [解析] ∵已知∠ABC=∠DCB,且BC=CB,
∴若添加①∠A=∠D,则可由“AAS”判定△ABC≌△DCB;
若添加②AC=DB,则属于“SSA”,不能判定△ABC≌△DCB;
若添加③AB=DC,则可由“SAS”判定△ABC≌△DCB.
13. 【答案】∠A=∠C或∠B=∠D或AB∥CD(答案不唯一)
[解析] 由题意可知∠AOB=∠COD,AB=CD.
∵AB是∠AOB的对边,CD是∠COD的对边,∴只能添加角相等,故可添加∠A=∠C或∠B=∠D或AB∥CD.
14. 【答案】20
15. 【答案】②
【解析】∵已知,且,
∴若添加①,则可由AAS判定≌;
若添加②,则属于边边角的顺序,不能判定≌;
若添加③,则属于边角边的顺序,可以判定≌.
故答案为:②.
16. 【答案】16 [解析] ∵BF∥AC,
∴∠EBF=∠EAD.
在△BFE和△ADE中,
∴△BFE≌△ADE(ASA).∴BF=AD.
∴BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD.
∵当FD⊥AC时,FD最短,此时FD=BC=5,
∴四边形FBCD周长的最小值为5+11=16.
三、解答题
17. 【答案】
证明:∵AE=BF,∴AE+EF=BF+EF,
即AF=BE.
∵AC∥BD,∴∠CAF=∠DBE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS).
∴CF=DE.
18. 【答案】
证明:(1)∵BE⊥AC,CD⊥AB,
∴∠AEB=∠ADC=90°.
在△AEB与△ADC中,
∴△AEB≌△ADC(AAS).
(2)∵△AEB≌△ADC,∴AE=AD.
在Rt△AEF与Rt△ADF中,
∴Rt△AEF≌Rt△ADF(HL).
∴∠EAF=∠DAF.∴AF平分∠BAC.
19. 【答案】
解:(1)∵AD∥BC,AB⊥BC,
∴∠ABC=∠BAD=90°.
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠AED=90°.
∴∠ABF+∠BAF=∠BAF+∠DAE=90°.
∴∠DAE=∠ABF=63°.∴∠ADE=27°.
(2)证明:由(1)得∠DAE=∠ABF,∠AED=∠BFA=90°.
在△DAE和△ABF中,
∴△DAE≌△ABF(AAS).
∴AE=BF,DE=AF.
∴DE=AF=AE+EF=BF+EF.
20. 【答案】
证明:∵在?ABCD中,∠BAD=∠BCD,AB∥CD,
∴∠E=∠F,180°-∠BAD=180°-∠BCD,即∠EAG=∠FCH,(5分)
在△AEG和△CFH中,
,
∴△AEG≌△CFH(ASA).(7分)
21. 【答案】
解:(1)证明:由题意得AC=CB,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°.
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°.∴∠BCE=∠CAD.
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS).
(2)由(1)知△ADC≌△CEB,
∴AD=CE=4a=40 cm,CD=BE=3a=30 cm.
∴DE=70 cm.
∴S△ABC=×(30+40)×70-2××30×40=1250(cm2).
答:三角板ABC的面积为1250 cm2.
